浙江省嘉兴市海宁新仓中学2022-2023学年数学七下期末学业水平测试试题含答案

这是一份浙江省嘉兴市海宁新仓中学2022-2023学年数学七下期末学业水平测试试题含答案，共8页。
浙江省嘉兴市海宁新仓中学2022-2023学年数学七下期末学业水平测试试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。3．考试结束后，将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1．学习勾股定理时，数学兴趣小组设计并组织了“勾股定理的证明”的比赛，全班同学的比赛得分统计如表：得分（分60708090100人数（人8121073则得分的中位数和众数分别为　　A．75，70 B．75，80 C．80，70 D．80，802．下列结论中正确的有  （   ）①若一个三角形中最大的角是80°，则这个三角形是锐角三角形②三角形的角平分线、中线和高都在三角形内部 ③一个三角形最少有一个角不小于60°④一个等腰三角形一定是钝角三角形A．1个 B．2个 C．3个 D．4个3．甲、乙、丙、丁四名同学在一次投掷实心球训练中，在相同条件下各投掷10次，他们成绩的平均数与方差s2如下表：若要选一名成绩好且发挥稳定的同学参加比赛，则应该选择（　　）A．甲 B．乙 C．丙 D．丁4．将0.000008这个数用科学记数法表示为（   ）A．8×10-6 B．8×10-5 C．0.8×10-5 D．8×10-75．在平面直角坐标系中,线段AB两端点的坐标分别为A(1,0),B(3,2).将线段AB平移后,A、B的对应点的坐标可以是(   )A．(1,−1),(−1,−3) B．(1,1),(3,3) C．(−1,3),(3,1) D．(3,2),(1,4)6．下列边长相等的正多边形的组合中，不能镶嵌平面的是（    ）A．正三角形和正方形 B．正三角形和正六边形C．正方形和正八边形 D．正五边形和正方形7．如图，矩形ABCD中，O是对角线AC的中点，OE⊥AC，交AD于点E，连接CE．若AB＝2，BC＝4，则CE的长为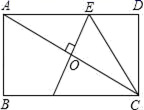（　　）A．2.5 B．2.8 C．3 D．3.58．如图，在10×6的网格中，每个小方格的边长都是1个单位，将△ABC平移到△DEF的位置，下面正确的平移步骤是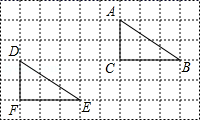（    ）A．先把△ABC向左平移5个单位，再向下平移2个单位B．先把△ABC向右平移5个单位，再向下平移2个单位C．先把△ABC向左平移5个单位，再向上平移2个单位D．先把△ABC向右平移5个单位，再向上平移2个单位9．以下列各组数据中的三个数作为三角形的边长，其中能构成直角三角形的是（   ）A．2，3，4 B．， ，  C．1， ，2 D．7，8，910．如图，已知△ACD∽△ADB，AC=4，AD=2，则AB的长为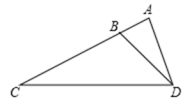A．1 B．2C．3 D．4二、填空题(本大题共有6小题，每小题3分，共18分)11．若一元二次方程的两个根分别是矩形的边长,则矩形对角线长为______.12．9的算术平方根是     ．13．如图所示,数轴上点A所表示的数为____.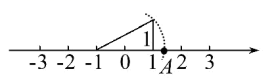14．为预防传染病，某校定期对教室进行“药熏消毒”，已知药物燃烧阶段，室内每立方米空气中的含药量与燃烧时间（分钟）成正比例；烧灼后，与成反比例（如图所示）.现测得药物分钟燃烧完，此时教室内每立方米空气含药量为.研究表明当每立方米空气中含药量低于时，对人体方能无毒作用，那么从消毒开始，至少需要经过______分钟后，学生才能回到教室.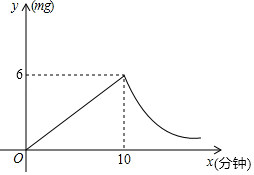15．在甲、乙、丙、丁四人进行射击测试，每人10次射击成绩的平均数均是9.2环，方差分别为＝0.56，＝0.60，＝0.45，＝0.50，则成绩最稳定的是______.16．如图，已知在△ABC中，BC边上的高AD与AC边上的高BE交于点F，且∠BAC=45°，BD=6，CD=4，则△ABC的面积为_____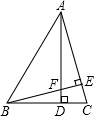．三、解下列各题(本大题共8小题，共72分)17．（8分）已知：如图，在□ABCD中，对角线AC，BD相交于点O，直线EF过点O，交DA于点E，交BC于点F.求证：OE＝OF，AE＝CF，DE＝BF 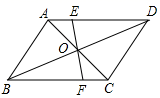  18．（8分）据大数据统计显示，某省2016年公民出境旅游人数约100万人次，2017年与2018年两年公民出境旅游总人数约264万人次，若这两年公民出境旅游总人数逐年递增，请解答下列问题：（1）求这两年该省公民出境旅游人数的年平均增长率；（2）如果2019年仍保持相同的年平均增长率，请你预测2019年该省公民出境旅游人数约多少万人次？   19．（8分）如图，四边形 ABCD 为平行四边形，AD＝a，BE∥AC，DE 交AC的延长线于F点，交BE于E点． （1）求证：DF＝FE ； （2）若 AC＝2CF，∠ADC＝60°，AC⊥DC，求BE的长； （3）在（2）的条件下，求四边形ABED的面积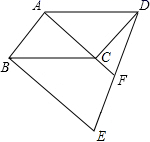．    20．（8分）在一条笔直的公路上有A、B、C三地，C地位于A、B两地之间，甲车从A地沿这条公路匀速驶向C地，乙车从B地沿这条公路匀速驶向A地，在甲车出发至甲车到达C地的过程中，甲、乙两车各自与C地的距离y（公里）与甲车行驶时间（小时）之间的函数关系如图，请根据所给图象关系解答下列问题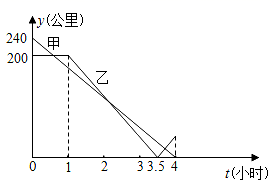：（1）求甲、乙两车的行驶速度；（2）求乙车出发1.5小时后，两车距离多少公里？（3）求乙车出发多少小时后，两车相遇？   21．（8分）几何学的产生，源于人们对土地面积测量的需要，以面积早就成为人们认识图形性质与几何证明的有效工具，可以说几何学从一开始便与面积结下了不解之缘．我们已经掌握了平行四边形面积的求法，但是一般四边形的面积往往不易求得，那么我们能否将其转化为平行四边形来求呢？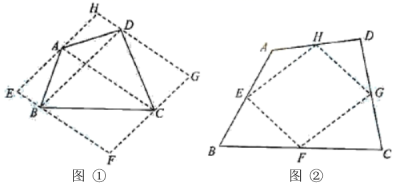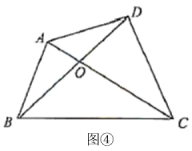（1）方法1：如图①，连接四边形的对角线，，分别过四边形的四个顶点作对角线的平行线，所作四条线相交形成四边形，易证四边形是平行四边形．请直接写出S四边形ABCD和之间的关系：_______________．方法2：如图②，取四边形四边的中点，，，，连接，，，，（2）求证：四边形是平行四边形；（3）请直接写出S四边形ABCD与之间的关系：_____________．方法3：如图③，取四边形四边的中点，，，，连接，交于点．先将四边形绕点旋转得到四边形，易得点，，在同一直线上；再将四边形绕点旋转得到四边形，易得点，，在同一直线上；最后将四边形沿方向平移，使点与点重合，得到四边形；（4）由旋转、平移可得_________，_________，所以，所以点，，在同一直线上，同理，点，，也在同一点线上，所以我们拼接成的图形是一个四边形．（5）求证：四边形是平行四边形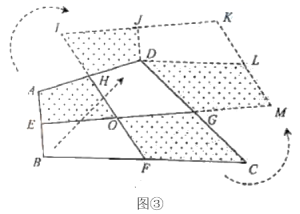．（注意：请考生在下面2题中任选一题作答如果多做，则按所做的第一题计分）（6）应用1：如图④，在四边形中，对角线与交于点，，，，则S四边形ABCD=            ．（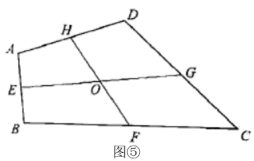7）应用2：如图⑤，在四边形中，点，，，分别是，，，的中点，连接，交于点，，，，则S四边形ABCD=___________   22．（10分）如图，四边形ABCD是平行四边形，分别以AB，CD为边向外作等边△ABE和△CDF，连接AF，CE．求证：四边形AECF为平行四边形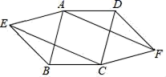．   23．（10分）高铁的开通给滕州人民出行带来极大的方便，从滕州到北京相距，现在乘高铁列车比以前乘特快列车少用，已知高铁列车的平均速度是特快列车的2.8倍，求高铁列车的平均行驶速度．   24．（12分）（1）已知一次函数的图象经过，两点.求这个一次函数的解析式；并判断点是否在这个一次函数的图象上；（2）如图所示，点D是等边内一点，，，，将绕点A逆时针旋转到的位置，求的周长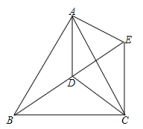．   参考答案 一、选择题(每小题3分,共30分)1、A2、B3、A4、A5、B6、D7、A8、A9、C10、A 二、填空题(本大题共有6小题，每小题3分，共18分)11、112、1．13、14、115、丙16、1 三、解下列各题(本大题共8小题，共72分)17、证明见解析18、 (1)这两年公民出境旅游总人数的年平均增长率为20%；(2)约172.8万人次.19、（1）证明见解析（2） （3） 20、（1）甲车的行驶速度 60（km/h），乙车的行驶速度80（km/h）；（2）两车距离170公里；（3）乙车出发小时后，两车相遇.21、（1）S四边形ABCD；（2）见详解；（1）S四边形ABCD ；（4）AEO，OEB；（5）见详解；（6）；（7）22、见解析.23、高铁列车平均速度为．24、（1）点P不在这个一次函数的图象上；（2）的周长．