


福建省厦门市音乐学校2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案
展开
这是一份福建省厦门市音乐学校2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案,共6页。
福建省厦门市音乐学校2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象与
的图象与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,且点
,且点![]() 在
在![]() 的内部,则
的内部,则![]() 的取值范围是( )
的取值范围是( )  A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 或
或![]() 2.如图,直线
2.如图,直线![]() 与
与![]() 分别交x轴于点
分别交x轴于点![]() ,
,![]() ,则不等式
,则不等式![]() 的解集为( )
的解集为( )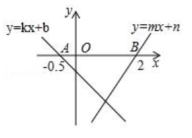 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 或
或![]() 3.若反比例函数y=
3.若反比例函数y=![]() 的图象位于第二、四象限,则k的取值可能是( )A.﹣1 B.1 C.2 D.34.已知
的图象位于第二、四象限,则k的取值可能是( )A.﹣1 B.1 C.2 D.34.已知![]() 是方程组
是方程组 ![]() 的解,则a+b的值为 ( )A.2 B.-2 C.4 D.-45.已知a<b,则下列不等式一定成立的是( )A.a+3>b+3 B.2a>2b C.﹣a<﹣b D.a﹣b<06.如图,将一个含有
的解,则a+b的值为 ( )A.2 B.-2 C.4 D.-45.已知a<b,则下列不等式一定成立的是( )A.a+3>b+3 B.2a>2b C.﹣a<﹣b D.a﹣b<06.如图,将一个含有![]() 角的直角三角板的直角顶点放在一张宽为
角的直角三角板的直角顶点放在一张宽为![]() 的矩形纸带边沿上,另一个顶点在纸带的另一边沿上,若测得三角板的一边与纸带的一边所在的直线成
的矩形纸带边沿上,另一个顶点在纸带的另一边沿上,若测得三角板的一边与纸带的一边所在的直线成![]() 角,则三角板最长的长是( )
角,则三角板最长的长是( )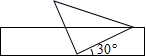 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 7.一个多边形的每个内角均为108º,则这个多边形是( )A.七边形 B.六边形 C.五边形 D.四边形8.如图,在
7.一个多边形的每个内角均为108º,则这个多边形是( )A.七边形 B.六边形 C.五边形 D.四边形8.如图,在![]() 中,点
中,点![]() 、
、![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 、
、![]() 上,且
上,且![]() ,
,![]() .下列说法中不正确的是( )
.下列说法中不正确的是( )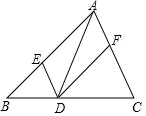 A.四边形
A.四边形![]() 是平行四边形B.如果
是平行四边形B.如果![]() ,那么四边形
,那么四边形![]() 是矩形.C.如果
是矩形.C.如果![]() 平分
平分![]() ,那么四边形
,那么四边形![]() 是正方形.D.如果
是正方形.D.如果![]() 且
且![]() ,那么四边形
,那么四边形![]() 是菱形.9.如图,一根木棍斜靠在与地面OM垂直的墙面ON上,设木棍中点为P,若木棍A端沿墙下滑,且B沿地面向右滑行.在此滑动过程中,点P到墙角点O的距离( )
是菱形.9.如图,一根木棍斜靠在与地面OM垂直的墙面ON上,设木棍中点为P,若木棍A端沿墙下滑,且B沿地面向右滑行.在此滑动过程中,点P到墙角点O的距离( ) 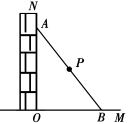 A.不变 B.变小 C.变大 D.先变大后变小10.如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=53°,则∠BCE的度数为( )
A.不变 B.变小 C.变大 D.先变大后变小10.如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=53°,则∠BCE的度数为( )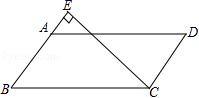
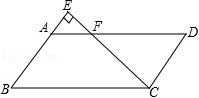 A.53° B.37° C.47° D.123°11.如图,
A.53° B.37° C.47° D.123°11.如图,![]() ,
,![]() ,
,![]() 三点在正方形网格线的交点处,若将
三点在正方形网格线的交点处,若将![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,则
,则![]() 点的坐标为( )
点的坐标为( )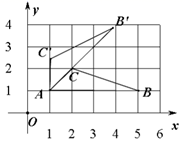 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 12.如图,菱形ABCD中,∠A是锐角,E为边AD上一点,△ABE沿着BE折叠,使点A的对应点F恰好落在边CD上,连接EF,BF,给出下列结论:①若∠A=70°,则∠ABE=35°;②若点F是CD的中点,则S△ABE
12.如图,菱形ABCD中,∠A是锐角,E为边AD上一点,△ABE沿着BE折叠,使点A的对应点F恰好落在边CD上,连接EF,BF,给出下列结论:①若∠A=70°,则∠ABE=35°;②若点F是CD的中点,则S△ABE![]() S菱形ABCD下列判断正确的是( )
S菱形ABCD下列判断正确的是( )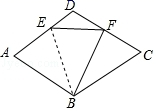 A.①,②都对 B.①,②都错 C.①对,②错 D.①错,②对二、填空题(每题4分,满分20分,将答案填在答题纸上)13.若
A.①,②都对 B.①,②都错 C.①对,②错 D.①错,②对二、填空题(每题4分,满分20分,将答案填在答题纸上)13.若![]() 有增根,则m=______14.若最简二次根式
有增根,则m=______14.若最简二次根式![]() 与
与![]() 能合并成一项,则a=_____.15.函数
能合并成一项,则a=_____.15.函数![]() 的图像与
的图像与![]() 如图所示,则k=__________.
如图所示,则k=__________.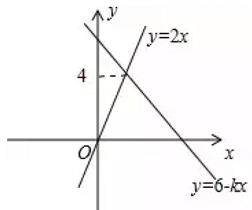 16.当x=_____时,分式
16.当x=_____时,分式![]() 的值为零.17.在菱形ABCD中,E为AB的中点,OE=3,则菱形ABCD的周长为.
的值为零.17.在菱形ABCD中,E为AB的中点,OE=3,则菱形ABCD的周长为.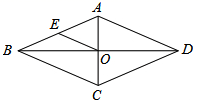 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)解方程(1)
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)解方程(1)![]() (2)
(2)![]() (3)
(3)![]() 19.(5分)已知,如图,点E为▱ABCD内任意一点,若▱ABCD的面积为6,连结点E与▱ABCD的四个顶点,求图中阴影部分的面积.
19.(5分)已知,如图,点E为▱ABCD内任意一点,若▱ABCD的面积为6,连结点E与▱ABCD的四个顶点,求图中阴影部分的面积.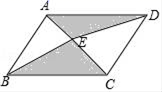 20.(8分)如图,已知线段a,b,∠α(如图).(1)以线段a,b为一组邻边作平行四边形,这样的平行四边形能作____个.(2)以线段a,b为一组邻边,它们的夹角为∠α,作平行四边形,这样的平行四边形能作_____个,作出满足条件的平行四边形(要求仅用直尺和圆规,保留作图痕迹,不写做法)
20.(8分)如图,已知线段a,b,∠α(如图).(1)以线段a,b为一组邻边作平行四边形,这样的平行四边形能作____个.(2)以线段a,b为一组邻边,它们的夹角为∠α,作平行四边形,这样的平行四边形能作_____个,作出满足条件的平行四边形(要求仅用直尺和圆规,保留作图痕迹,不写做法)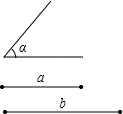 21.(10分)如图,正方形网格的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上.(1)分别求出AB,BC,AC的长;(2)试判断△ABC是什么三角形,并说明理由.
21.(10分)如图,正方形网格的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上.(1)分别求出AB,BC,AC的长;(2)试判断△ABC是什么三角形,并说明理由.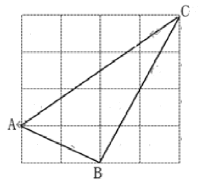 22.(10分)一组数据:1,1,2,5,x的平均数是1.(1)求x的值;(2)求这组数据的方差. 23.(12分)如果一个多位自然数的任意两个相邻数位上,右边数位上的数总比左边数位上的数大1,则我们称这样的自然数叫“美数”,例如:123,3456,67,…都是“美数”.(1)若某个三位“美数”恰好等于其个位的76倍,这个“美数”为 .(2)证明:任意一个四位“美数”减去任意一个两位“美数”之差再减去1得到的结果定能被11整除;(3)如果一个多位自然数的任意两个相邻数位上,左边数位上的数总比右边数位上的数大1,则我们称这样的自然数叫“妙数”,若任意一个十位为
22.(10分)一组数据:1,1,2,5,x的平均数是1.(1)求x的值;(2)求这组数据的方差. 23.(12分)如果一个多位自然数的任意两个相邻数位上,右边数位上的数总比左边数位上的数大1,则我们称这样的自然数叫“美数”,例如:123,3456,67,…都是“美数”.(1)若某个三位“美数”恰好等于其个位的76倍,这个“美数”为 .(2)证明:任意一个四位“美数”减去任意一个两位“美数”之差再减去1得到的结果定能被11整除;(3)如果一个多位自然数的任意两个相邻数位上,左边数位上的数总比右边数位上的数大1,则我们称这样的自然数叫“妙数”,若任意一个十位为![]()
![]() 为整数)的两位“妙数”和任意一个个位为
为整数)的两位“妙数”和任意一个个位为![]() 为整数)的两位“美数”之和为55,则称两位数
为整数)的两位“美数”之和为55,则称两位数![]() 为“美妙数”,并把这个“美妙数”记为
为“美妙数”,并把这个“美妙数”记为![]() ,则求
,则求![]() 的最大值. 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、A2、D3、A4、B5、D6、D7、C8、C9、A10、B11、C12、A 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、-114、215、
的最大值. 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、A2、D3、A4、B5、D6、D7、C8、C9、A10、B11、C12、A 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、-114、215、![]() 16、117、1. 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)
16、117、1. 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)![]() (2)
(2)![]() (3)
(3)![]() 19、120、 (1)无数;(2)图形见解析;1.21、(1)
19、120、 (1)无数;(2)图形见解析;1.21、(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() 是直角三角形,理由见解析22、(1)x=4;(2)2.23、 (1)456 (2)见解析 (3)42
是直角三角形,理由见解析22、(1)x=4;(2)2.23、 (1)456 (2)见解析 (3)42
相关试卷
这是一份2023-2024学年福建省厦门市竹坝学校数学八上期末质量跟踪监视试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,如图,线段关于轴对称的线段是,计算,已知是正比例函数,则m的值是等内容,欢迎下载使用。
这是一份2023-2024学年福建省厦门市海沧区鳌冠学校数学八上期末质量跟踪监视模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,在平面直角坐标系中,点P等内容,欢迎下载使用。
这是一份2023-2024学年福建省厦门市九年级数学第一学期期末质量跟踪监视模拟试题,共19页。试卷主要包含了下列方程中,是一元二次方程的是,抛物线 y=等内容,欢迎下载使用。









