


聊城市重点中学2022-2023学年七下数学期末质量检测试题含答案
展开聊城市重点中学2022-2023学年七下数学期末质量检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1.如图,将![]() 个全等的阴影小正方形摆放得到边长为
个全等的阴影小正方形摆放得到边长为![]() 的正方形
的正方形![]() ,中间小正方形的各边的中点恰好为另外
,中间小正方形的各边的中点恰好为另外![]() 个小正方形的一个顶点,小正方形的边长为
个小正方形的一个顶点,小正方形的边长为![]() (
(![]() 、
、![]() 为正整数),则
为正整数),则![]() 的值为( )
的值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.如图,已知点P是∠AOB平分线上的一点,∠AOB=60°,PD⊥OA ,M是OP的中点,DM=4 cm.若点C是OB上一个动点,则PC的最小值为( )cm.
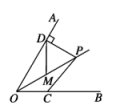
A.7 B.6 C.5 D.4
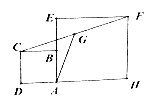
3.如图,矩形ABCD中,AB=7,BC=4,按以下步骤作图:以点B为圆心,适当长为半径画弧,交AB,BC于点E,F;再分别以点E,F为圆心,大于![]() EF的长为半径画弧,两弧在∠ABC内部相交于点H,作射线BH,交DC于点G,则DG的长为( )
EF的长为半径画弧,两弧在∠ABC内部相交于点H,作射线BH,交DC于点G,则DG的长为( )
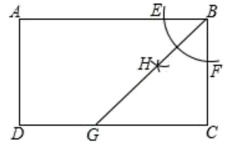
A.1 B.1![]() C.3 D.2
C.3 D.2![]()
4.如图,四边形ABCD是菱形,圆O经过点A、C、D,与BC相交于点E,连接AC、AE.若![]() ,则
,则![]() ( )
( )
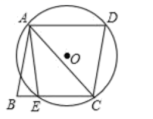
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知直线l:y=-![]() x+1与x轴交于点P,将l绕点P顺时针旋转90°得到直线l′,则直线l′的解析式为( )
x+1与x轴交于点P,将l绕点P顺时针旋转90°得到直线l′,则直线l′的解析式为( )
A.y=![]() x-1 B.y=2x-1 C.y=
x-1 B.y=2x-1 C.y=![]() x-4 D.y=2x-4
x-4 D.y=2x-4
6.下列命题是假命题的是( )
A.两直线平行,同位角相等 B.两组对角分别相等的四边形是平行四边形
C.若![]() ,则
,则![]() D.若
D.若![]() ,则
,则![]()
7.下列代数式属于分式的是( )
A.![]() B.3y C.
B.3y C.![]() D.
D.![]() +y
+y
8.下列四个图形中,既是轴对称又是中心对称的图形是( ) 
A.4个 B.3个 C.2个 D.1个
9.下列图形不是中心对称图形的是![]()
![]()
A. B.
B. C.
C. D.
D.
10.如图,平行四边形![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 的周长是( )
的周长是( )
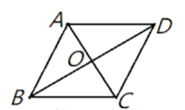
A.7.5 B.12 C.6 D.无法确定
二、填空题(本大题共有6小题,每小题3分,共18分)
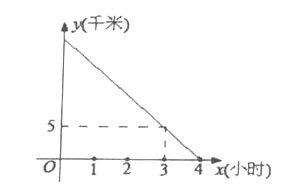
11.小明从A地出发匀速走到B地.小明经过![]() (小时)后距离B地
(小时)后距离B地![]() (千米)的函数图像如图所示.则A、B两地距离为_________千米.
(千米)的函数图像如图所示.则A、B两地距离为_________千米.
12.如图,将一个![]() 智屏手机抽象成一个的矩形
智屏手机抽象成一个的矩形![]() ,其中
,其中![]() ,
,![]() ,然后将它围绕顶点
,然后将它围绕顶点![]() 逆时针旋转一周,旋转过程中
逆时针旋转一周,旋转过程中![]() 、
、![]() 、
、![]() 、
、![]() 的对应点依次为
的对应点依次为![]() 、
、![]() 、
、![]() 、
、![]() ,则当
,则当![]() 为直角三角形时,若旋转角为
为直角三角形时,若旋转角为![]() ,则
,则![]() 的大小为______.
的大小为______.
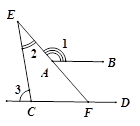
13.如图,AB∥CD,则∠1+∠3—∠2的度数等于 __________.
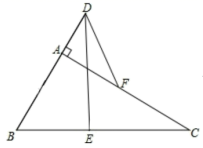
14.如图,在![]() 中
中![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,延长
的中点,延长![]() 到点
到点![]() ,使
,使![]() ,则
,则![]() _____________.
_____________.
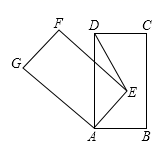
15.如图放置的两个正方形的边长分别为![]() 和
和![]() ,点
,点![]() 为
为![]() 中点,则
中点,则![]() 的长为__________.
的长为__________.
16.如果一次函数的图像经过点![]() 和
和![]() ,那么函数值
,那么函数值![]() 随着自变量
随着自变量![]() 的增大而__________.(填“增大”或“不变”或“减小”)
的增大而__________.(填“增大”或“不变”或“减小”)
三、解下列各题(本大题共8小题,共72分)
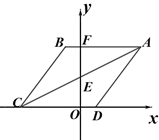
17.(8分)如图O为坐标原点,四边形ABCD是菱形,A(4,4),B点在第二象限,AB=5,AB与y轴交于点F,对角线AC交y轴于点E
(1)直接写出B、C点的坐标;
(2)动点P从C点出发以每秒1个单位的速度沿折线段C﹣D﹣A运动,设运动时间为t秒,请用含t的代数式表示△EDP的面积;
(3)在(2)的条件下,是否存在一点P,使△APE沿其一边翻折构成的四边形是菱形?若存在,请直接写出当t为多少秒时存在符合条件的点P;若不存在,请说明理由.
18.(8分)观摩、学习是我们生活的一部分,而在观摩中与展览品保持一定的距离是一种文明的表现.某学校数学业余学习小组在平面直角坐标系xOy有关研讨中,将到线段PQ所在的直线距离为![]() 的直线,称为直线PQ的“观察线”,并称观察线上到P、Q两点距离和最小的点L为线段PQ的“最佳观察点”.
的直线,称为直线PQ的“观察线”,并称观察线上到P、Q两点距离和最小的点L为线段PQ的“最佳观察点”.
(1)如果P(1,![]() ),Q(4,
),Q(4,![]() ),那么在点A(1,0),B(
),那么在点A(1,0),B(![]() ,2
,2![]() ),C(
),C(![]() ,3)中,处在直线PQ的“观察线”上的是点 ;
,3)中,处在直线PQ的“观察线”上的是点 ;
(2)求直线y=![]() x的“观察线”的表达式;
x的“观察线”的表达式;
(3)若M(0,﹣1),N在第二象限,且MN=6,当MN的一个“最佳观察点”在y轴正半轴上时,直接写出点N的坐标;并按逆时针方向联结M、N及其所有“最佳观察点”,直接写出联结所围成的多边形的周长和面积.
19.(8分)如图,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点
的图象交于点![]() ,
,![]() ,点
,点![]() 的横坐标实数4,点
的横坐标实数4,点![]() 在反比例函数
在反比例函数![]() 的图象上.
的图象上.
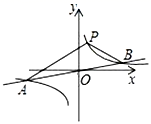
(1)求反比例函数的表达式;
(2)观察图象回答:当![]() 为何范围时,
为何范围时,![]() ;
;
(3)求![]() 的面积.
的面积.
20.(8分)取一张长与宽之比为![]() 的长方形纸板,剪去四个边长为
的长方形纸板,剪去四个边长为![]() 的小正方形(如图),并用它做一个无盖的长方体形状的包装盒,要使包装盒的容积为
的小正方形(如图),并用它做一个无盖的长方体形状的包装盒,要使包装盒的容积为![]() (纸板的厚度略去不计),这张长方形纸板的长与宽分别为多少厘米?
(纸板的厚度略去不计),这张长方形纸板的长与宽分别为多少厘米?

21.(8分)甲、乙两台机床同时生产一种零件.在连续![]() 周中,两台机床每周出次品的数量如下表.
周中,两台机床每周出次品的数量如下表.
甲 |
|
|
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
|
|
(1)分别计算两组数据的平均数与方差;
(2)两台机床出次品的平均数怎样?哪台机床出次品的波动性小?
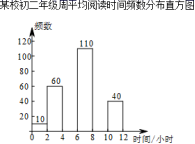
22.(10分)《北京中小学语文学科教学21条改进意见》中的第三条指出:“在教学中重视对国学经典文化的学习,重视历史文化的熏陶,加强与革命传统教育的结合,使学生了解中华文化的悠久历史,增强民族文化自信和价值观自信,使语文教学成为涵养社会主义核心价值观的重要源泉之一”.为此,昌平区掀起了以“阅读经典作品,提升思维品质”为主题的读书活动热潮,在一个月的活动中随机调查了某校初二年级学生的周人均阅读时间的情况,整理并绘制了如下的统计图表:
某校初二年级学生周人均阅读时间频数分布表
周人均阅读时间x (小时) | 频数 | 频率 |
0≤x<2 | 10 | 0.025 |
2≤x<4 | 60 | 0.150 |
4≤x<6 | a | 0.200 |
6≤x<8 | 110 | 0.275 |
8≤x<10 | 100 | 0.250 |
10≤x<12 | 40 | b |
合计 | 400 | 1.000 |
请根据以上信息,解答下列问题:
(1)在频数分布表中a=______,b=______;
(2)补全频数分布直方图;
(3)若该校有1600名学生,根据调查数据请你估计,该校学生周人均阅读时间不少于6小时的学生大约有______人.
23.(10分)端午节前夕,小东妈妈准备购买若干个粽子和咸鸭蛋(每个棕子的价格相同,每个咸鸭蛋的价格相同).已知某超市粽子的价格比咸鸭蛋的价格贵1.8元,小东妈妈发现,花30元购买粽子的个数与花12元购买的咸鸭蛋个数相同.
(1)求该超市粽子与咸鸭蛋的价格各是多少元?
(2)小东妈妈计划购买粽子与咸鸭蛋共18个,她的一张购物卡上还有余额40元,若只用这张购物卡,她最多能购买粽子多少个?
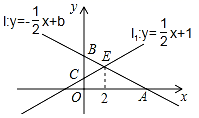
24.(12分)如图,已知直线l:y=﹣![]() x+b与x轴,y轴的交点分别为A,B,直线l1:y=
x+b与x轴,y轴的交点分别为A,B,直线l1:y=![]() x+1与y轴交于点C,直线l与直线ll的交点为E,且点E的横坐标为1.
x+1与y轴交于点C,直线l与直线ll的交点为E,且点E的横坐标为1.
(1)求实数b的值和点A的坐标;
(1)设点D(a,0)为x轴上的动点,过点D作x轴的垂线,分别交直线l与直线ll于点M、N,若以点B、O、M、N为顶点的四边形是平行四边形,求a的值.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、D
3、C
4、B
5、D
6、D
7、C
8、C
9、D
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、20
12、![]() 或
或![]() 或
或![]()
13、180°
14、2
15、![]()
16、增大
三、解下列各题(本大题共8小题,共72分)
17、 (1)B(-1,4),C(-4,0);![]() 见解析;(3)
见解析;(3)![]() 或7.5.
或7.5.
18、 (1)A,B; (1)直线y=![]() x的“观察线”的解析式为y=
x的“观察线”的解析式为y=![]() x﹣1或y=
x﹣1或y=![]() x+1;(3)围成的图形是菱形MQNQ′,这个菱形的周长8
x+1;(3)围成的图形是菱形MQNQ′,这个菱形的周长8![]() ,这个菱形的面积6
,这个菱形的面积6![]() .
.
19、(1)反比例函数的表达式为y=![]() ;(2)x<﹣2或0<x<2时,y1>y2;(3)△PAB的面积为1.
;(2)x<﹣2或0<x<2时,y1>y2;(3)△PAB的面积为1.
20、长为30厘米,宽为12厘米
21、(1)甲的平均数为:![]() ;乙的平均数为:
;乙的平均数为:![]() ;甲的方差为:
;甲的方差为:![]() ;乙的方差为:
;乙的方差为:![]() ;
;
(2)两台机床出次品的平均数相同;甲机床出次品的波动性小.
22、(1)80,0.100;(2)见解析;(3)1.
23、(1)咸鸭蛋的价格为1.2元,粽子的价格为3元(2)她最多能购买粽子10个
24、(3)b=2,A(6,0);(3) a的值为5或﹣3
长治市重点中学2022-2023学年七下数学期末质量检测模拟试题含答案: 这是一份长治市重点中学2022-2023学年七下数学期末质量检测模拟试题含答案,共6页。试卷主要包含了下列各式运算结果为x8的是,如图,在中,于点若则等于,下列代数式属于分式的是等内容,欢迎下载使用。
榆林市重点中学2022-2023学年数学七下期末质量检测模拟试题含答案: 这是一份榆林市重点中学2022-2023学年数学七下期末质量检测模拟试题含答案,共7页。试卷主要包含了如图,点A等内容,欢迎下载使用。
拉萨市重点中学2022-2023学年七下数学期末质量检测模拟试题含答案: 这是一份拉萨市重点中学2022-2023学年七下数学期末质量检测模拟试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,下列因式分解正确的是等内容,欢迎下载使用。












