龙岩市重点中学2022-2023学年七年级数学第二学期期末教学质量检测模拟试题含答案

这是一份龙岩市重点中学2022-2023学年七年级数学第二学期期末教学质量检测模拟试题含答案，共7页。试卷主要包含了考生要认真填写考场号和座位序号等内容，欢迎下载使用。
龙岩市重点中学2022-2023学年七年级数学第二学期期末教学质量检测模拟试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 注意事项1．考生要认真填写考场号和座位序号。2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。 一、选择题(每小题3分,共30分)1．一组数据11、12、15、12、11，下列说法正确的是（　　）A．中位数是15 B．众数是12C．中位数是11、12 D．众数是11、122．如图，在中，，以顶点为圆心，适当长为半径画弧，分别交，于点，，再分别以点，为圆心，大于的长为半径画弧，两弧交于点，作射线交边于点，若，，则的面积是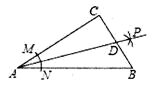（）A．15 B．30 C．45 D．603．已知边长分别为a、b的长方形的周长为10，面积4，则ab2+a2b的值为（　　）A．10 B．20 C．40 D．804．甲，乙两个样本的容量相同，甲样本的方差为0.102，乙样本的方差是0.06，那么（ ）A．甲的波动比乙的波动大 B．乙的波动比甲的波动大C．甲，乙的波动大小一样 D．甲，乙的波动大小无法确定5．已知一组数据3，a，4，5的众数为4，则这组数据的平均数为（ ）A．3 B．4 C．5 D．66．已知二次函数y= 2x2+8x-1的图象上有点A（-2，y1），B（-5，y2），C（-1，y3），则y1、y2、y3的大小关系为（    ）A． B． C． D．7．如图，一次函数y＝﹣x+4的图象与两坐标轴分别交于A、B两点，点C是线段AB上一动点（不与点A、B重合），过点C分别作CD、CE垂直于x轴、y轴于点D、E，当点C从点A出发向点B运动时，矩形CDOE的周长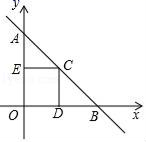（　　）A．逐渐变大 B．不变C．逐渐变小 D．先变小后变大8．在下列图形中，既是轴对称图形又是中心对称图形的是 （ ）A． B． C． D．9．如图，要测定被池塘隔开的A，B两点的距离．可以在AB外选一点C，连接AC，BC，并分别找出它们的中点D，E，连接DE．现测得AC＝30m，BC＝40m，DE＝24m，则AB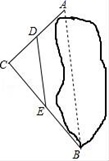＝（　　）A．50m B．48m C．45m D．35m10．为了解游客对恭王府、北京大观园、北京动物园和景山公园四个旅游景区的满意率情况，某班实践活动小组的同学给出了以下几种调查方案：方案一：在多家旅游公司随机调查400名导游；方案二：在恭王府景区随机调查400名游客；方案三：在北京动物园景区随机调查400名游客；方案四：在上述四个景区各随机调查400名游客．在这四种调查方案中，最合理的是（　　）A．方案一 B．方案二 C．方案三 D．方案四二、填空题(本大题共有6小题，每小题3分，共18分)11．函数中，自变量的取值范围是__________．12．    若10个数的平均数是3，方差是4，现将这10个数都扩大2倍，则这组新数据的方差是_____．13．如图，在正方形ABCD中，对角线AC，BD交于点O，E为OB上的点，∠EAB＝15°，若OE＝，则AB的长为__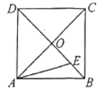．14．如图，在Rt△ABC中，∠C=90°，AC=4，将△ABC沿CB方向平移得到△DEF，若四边形ABED的面积等于8，则平移的距离为_____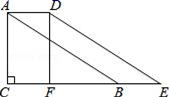．15．计算：﹣＝_____．16．若，则a与b的大小关系为a_____b(填“＞”、“＜”或“=”)三、解下列各题(本大题共8小题，共72分)17．（8分）某产品成本为400元/件，由经验得知销售量与售价是成一次函数关系，当售价为800元/件时能卖1000件，当售价1000元/件时能卖600件，问售价多少时利润最大？最大利润是多少？   18．（8分）某班级准备购买一些奖品奖励春季运动会表现突出的同学，奖品分为甲、乙两种，已知，购买一个甲奖品比一个乙奖品多用20元，若用400元购买甲奖品的个数是用160元购买乙奖品个数的一半.（1）求购买一个甲奖品和一个乙奖品各需多少元？（2）经商谈，商店决定给予该班级每购买甲奖品3个就赠送一个乙奖品的优惠，如果该班级需要乙奖品的个数是甲奖品的2倍还多8个，且该班级购买两种奖项的总费用不超过640元，那么该班级最多可购买多少个甲奖品？   19．（8分）某校为了解学生每天参加户外活动的情况，随机抽查了100名学生每天参加户外活动的时间情况，并将抽查结果绘制成如图所示的扇形统计图．请你根据图中提供的信息解答下列问题：（1）请直接写出图中的值，并求出本次抽查中学生每天参加户外活动时间的中位数；（2）求本次抽查中学生每天参加户外活动的平均时间．   20．（8分）如图，四边形ABCD是菱形，AC=24, BD=10,DH⊥AB 于点H，求菱形的面积及线段DH的长．   21．（8分）列方程解应用题:某地2016年为做好“精准扶贫”，投入资金1280万元用于异地安置，并规划投入资金逐年增加，2018年在2016年的基础上增加投入资金1600万元.从2016年到2018年，该地投入异地安置资金的年平均增长率为多少?   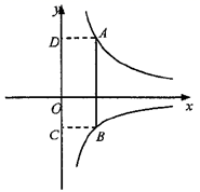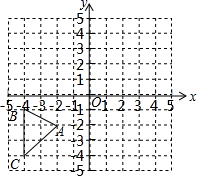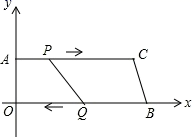22．（10分）（阅读理解）对于任意正实数、，∵，∴∴，只有当时，等号成立．（数学认识）在（、均为正实数）中，若为定值，则，只有当时，有最小值．（解决问题）（1）若时，当_____________时，有最小值为_____________；（2）如图，已知点在反比例函数的图像上，点在反比例函数的图像上，轴，过点作轴于点，过点作轴于点．求四边形周长的最小值．   23．（10分）如图，在平面直角坐标系中，△ABC各顶点的坐标分别为A(−2，−2)，B(−4，−1），C(−4，−4)．（1）作出ABC关于原点O成中心对称的A1B1C1.（2）作出点A关于x轴的对称点A'若把点A'向右平移a个单位长度后落在A1B1C1的内部（不包括顶点和边界），求a的取值范围.   24．（12分）如图，在四边形中，，顶点是原点，顶点在轴上，顶点的坐标为，,，点从点出发，以的速度向点运动，点从点同时出发，以的速度向点运动.规定其中一个动点到达端点时，另一个动点也随之停止运动；从运动开始，设点运动的时间为.求直线的函数解析式；当为何值时，四边形是矩形？   参考答案 一、选择题(每小题3分,共30分)1、D2、B3、B4、A5、B6、C7、B8、C9、B10、D 二、填空题(本大题共有6小题，每小题3分，共18分)11、x≥0且x≠112、113、314、115、16、= 三、解下列各题(本大题共8小题，共72分)17、售价为850元/件时，有最大利润405000元18、（1）购买一个甲奖品需元，买一个乙奖品需要元；（2）该班级最多可购买个甲奖品.19、（1）a=20%．本次抽查中学生每天参加活动时间的中位数是1；（2）本次抽查中学生每天参加户外活动的平均时间是1.175小时．20、21、从2015年到2017年，该地投入异地安置资金的年平均增长率为50%.22、（1）1,1；（1）2.23、见解析24、（1）；（2）为.