


贵州省毕节地区名校2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案
展开
这是一份贵州省毕节地区名校2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,五边形的内角和为,已知,则化简的结果是等内容,欢迎下载使用。
贵州省毕节地区名校2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1.矩形的对角线长为10,两邻边之比为3:4,则矩形的面积为( )A.12 B.24 C.48 D.502.已知点![]() 和点
和点![]() 在反比例函数
在反比例函数![]() 的图象上,若
的图象上,若![]() ,则( )A.
,则( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.对于反比例函数
3.对于反比例函数![]() ,下列说法中不正确的是( )A.x>0时,y随x增大而增大B.图像分布在第二第四象限C.图像经过点(1.-2)D.若点A(
,下列说法中不正确的是( )A.x>0时,y随x增大而增大B.图像分布在第二第四象限C.图像经过点(1.-2)D.若点A(![]() )B(
)B(![]() )在图像上,若
)在图像上,若![]() ,则
,则![]() 4.若反比例函数
4.若反比例函数![]() 图象上有两个点
图象上有两个点![]() ,设
,设![]() ,则
,则![]() 不经过第( )象限.A.一 B.二 C.三 D.四5.五边形的内角和为( )A.360° B.540° C.720° D.900°6.如图所示,圆柱的高AB=3,底面直径BC=3,现在有一只蚂蚁想要从A处沿圆柱表面爬到对角C处捕食,则它爬行的最短距离是( )
不经过第( )象限.A.一 B.二 C.三 D.四5.五边形的内角和为( )A.360° B.540° C.720° D.900°6.如图所示,圆柱的高AB=3,底面直径BC=3,现在有一只蚂蚁想要从A处沿圆柱表面爬到对角C处捕食,则它爬行的最短距离是( )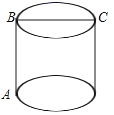 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 7.已知
7.已知![]() ,则化简
,则化简![]() 的结果是( )A.
的结果是( )A.![]() B.
B.![]() C.﹣3 D.38.图1长方形纸带,
C.﹣3 D.38.图1长方形纸带,![]() ,将纸带沿
,将纸带沿![]() 折叠成图2再沿
折叠成图2再沿![]() 折叠成图3,图3中的
折叠成图3,图3中的![]() 的度数是 .
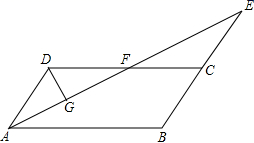
的度数是 .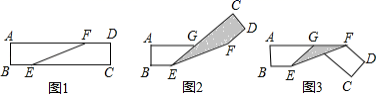 A.98° B.102° C.124° D.156°9.如图,在平行四边形ABCD中,
A.98° B.102° C.124° D.156°9.如图,在平行四边形ABCD中,![]() ,
,![]() 的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,
的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,![]() ,垂足为G,若
,垂足为G,若![]() ,则AE的边长为
,则AE的边长为![]()
![]()
 A.
A.![]() B.
B.![]() C.4 D.810.在
C.4 D.810.在![]() 中,对角线
中,对角线![]() 相交于点
相交于点![]() ,以点
,以点![]() 为坐标原点建立平面直角坐标系,其中
为坐标原点建立平面直角坐标系,其中![]() ,则点
,则点![]() 的坐标是( )A.
的坐标是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(本大题共有6小题,每小题3分,共18分)11.计算
二、填空题(本大题共有6小题,每小题3分,共18分)11.计算![]() =_____,(﹣
=_____,(﹣![]() )2=_____,3
)2=_____,3![]() ﹣
﹣![]() =_____.12.如图,在矩形ABCD中,AC为对角线,点E为BC上一点,连接AE,若∠CAD=2∠BAE,CD=CE=9,则AE的长为_____________.
=_____.12.如图,在矩形ABCD中,AC为对角线,点E为BC上一点,连接AE,若∠CAD=2∠BAE,CD=CE=9,则AE的长为_____________. 13.在平面直角坐标系中,一个智能机器人接到如下指令,从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m,其行走路线如图所示,第1次移动到
13.在平面直角坐标系中,一个智能机器人接到如下指令,从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m,其行走路线如图所示,第1次移动到![]() ,第2次移动到
,第2次移动到![]() ……,第n次移动到
……,第n次移动到![]() ,机器人移动第2018次即停止,则
,机器人移动第2018次即停止,则![]() 的面积是______.
的面积是______.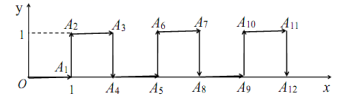 14.如图是甲、乙两名跳远运动员的10次测验成绩(单位:米)的折线统计图,观察图形,写出甲、乙这10次跳远成绩之间的大小关系:S甲2_____S乙2(填“>“或“<”)
14.如图是甲、乙两名跳远运动员的10次测验成绩(单位:米)的折线统计图,观察图形,写出甲、乙这10次跳远成绩之间的大小关系:S甲2_____S乙2(填“>“或“<”)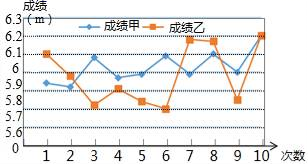 15.在平面直角坐标系xOy中,一次函数y=kx和y=﹣x+3的图象如图所示,则关于x的一元一次不等式kx<﹣x+3的解集是_____.
15.在平面直角坐标系xOy中,一次函数y=kx和y=﹣x+3的图象如图所示,则关于x的一元一次不等式kx<﹣x+3的解集是_____.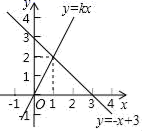 16.若整数x满足|x|≤3,则使
16.若整数x满足|x|≤3,则使![]() 为整数的x的值是 (只需填一个).三、解下列各题(本大题共8小题,共72分)17.(8分)已知:如图,在△ABC中,∠BAC的平分线AP与BC的垂直平分线PQ相交于点P,过点P分别作PM⊥AC于点M,PN⊥AB交AB延长线于点N,连接PB,PC.求证:BN=CM.
为整数的x的值是 (只需填一个).三、解下列各题(本大题共8小题,共72分)17.(8分)已知:如图,在△ABC中,∠BAC的平分线AP与BC的垂直平分线PQ相交于点P,过点P分别作PM⊥AC于点M,PN⊥AB交AB延长线于点N,连接PB,PC.求证:BN=CM.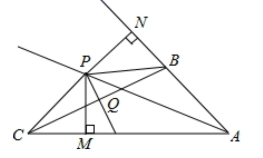 18.(8分)某中学八年级举行跳绳比赛,要求每班选出5名学生参加,在规定时间每人跳绳不低于150次为优秀,冠、亚军在八(1)、八(5)两班中产生.下表是这两个班的5名学生的比赛数据(单位:次) 1号2号3号4号5号平均数方差八(1)班13914815016015315046.8八(5)班150139145147169150103.2根据以上信息,解答下列问题:(1)求两班的优秀率及两班数据的中位数;(2)请你从优秀率、中位数和方差三方面进行简要分析,确定获冠军奖的班级. 19.(8分)某公司与销售人员签订了这样的工资合同:工资由两部分组成,一部分是基本工资,每人每月3000元;另一部分是按月销售量确定的奖励工资,每销售一件产品,奖励工资10元.设某销售员销售产品x件,他应得工资记为y元.(1)求y与x的函数关系式.(2)该销售员的工资为4100元,他这个月销售了多少件产品?(3)要使每月工资超过4500元,该月的销售量应当超过多少件? 20.(8分)如图,每个小正方形的边长都为1,四边形ABCD的顶点都在小正方形的顶点上.(1)求四边形ABCD的面积;(2)∠BCD是直角吗?说明理由.
18.(8分)某中学八年级举行跳绳比赛,要求每班选出5名学生参加,在规定时间每人跳绳不低于150次为优秀,冠、亚军在八(1)、八(5)两班中产生.下表是这两个班的5名学生的比赛数据(单位:次) 1号2号3号4号5号平均数方差八(1)班13914815016015315046.8八(5)班150139145147169150103.2根据以上信息,解答下列问题:(1)求两班的优秀率及两班数据的中位数;(2)请你从优秀率、中位数和方差三方面进行简要分析,确定获冠军奖的班级. 19.(8分)某公司与销售人员签订了这样的工资合同:工资由两部分组成,一部分是基本工资,每人每月3000元;另一部分是按月销售量确定的奖励工资,每销售一件产品,奖励工资10元.设某销售员销售产品x件,他应得工资记为y元.(1)求y与x的函数关系式.(2)该销售员的工资为4100元,他这个月销售了多少件产品?(3)要使每月工资超过4500元,该月的销售量应当超过多少件? 20.(8分)如图,每个小正方形的边长都为1,四边形ABCD的顶点都在小正方形的顶点上.(1)求四边形ABCD的面积;(2)∠BCD是直角吗?说明理由. 21.(8分)某土产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售.按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满.根据下表提供的信息,解答以下问题:土特产种类甲乙丙每辆汽车运载量(吨)865每吨土特产获利(百元)121610(1)设装运甲种土特产的车辆数为
21.(8分)某土产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售.按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满.根据下表提供的信息,解答以下问题:土特产种类甲乙丙每辆汽车运载量(吨)865每吨土特产获利(百元)121610(1)设装运甲种土特产的车辆数为![]() ,装运乙种土特产的车辆数为
,装运乙种土特产的车辆数为![]() ,求
,求![]() 与
与![]() 之间的函数关系式.(2)如果装运每辆土特产的车辆都不少于3辆,那么车辆的安排方案有几种?并写出每种安排方案.(3)若要使此次销售获利最大,应采用(2)中哪种安排方案?并求出最大利润的值. 22.(10分)如图,在平面直角坐标系
之间的函数关系式.(2)如果装运每辆土特产的车辆都不少于3辆,那么车辆的安排方案有几种?并写出每种安排方案.(3)若要使此次销售获利最大,应采用(2)中哪种安排方案?并求出最大利润的值. 22.(10分)如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,点
,点![]() 。
。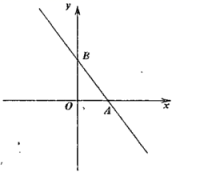 (1)求点
(1)求点![]() 和点
和点![]() 的坐标;(2)若点
的坐标;(2)若点![]() 在
在![]() 轴上,且
轴上,且![]() 求点
求点![]() 的坐标。(3)在
的坐标。(3)在![]() 轴是否存在点
轴是否存在点![]() ,使三角形
,使三角形![]() 是等腰三角形,若存在。请求出点
是等腰三角形,若存在。请求出点![]() 坐标,若不存在,请说明理由。 23.(10分)为创建“国家园林城市”,某校举行了以“爱我黄石”为主题的图片制作比赛,评委会对200名同学的参赛作品打分发现,参赛者的成绩x均满足50≤x<100,并制作了频数分布直方图,如图.
坐标,若不存在,请说明理由。 23.(10分)为创建“国家园林城市”,某校举行了以“爱我黄石”为主题的图片制作比赛,评委会对200名同学的参赛作品打分发现,参赛者的成绩x均满足50≤x<100,并制作了频数分布直方图,如图.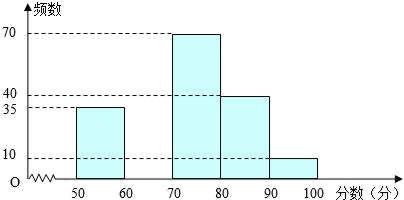 根据以上信息,解答下列问题:(1)请补全频数分布直方图;(2)若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?(3)比赛共设一、二、三等奖,若只有25%的参赛同学能拿到一等奖,则一等奖的分数线是多少? 24.(12分)再读教材:宽与长的比是
根据以上信息,解答下列问题:(1)请补全频数分布直方图;(2)若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?(3)比赛共设一、二、三等奖,若只有25%的参赛同学能拿到一等奖,则一等奖的分数线是多少? 24.(12分)再读教材:宽与长的比是 ![]() (约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)第一步,在矩形纸片一端.利用图①的方法折出一个正方形,然后把纸片展平.第二步,如图②.把这个正方形折成两个相等的矩形,再把纸片展平.
(约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)第一步,在矩形纸片一端.利用图①的方法折出一个正方形,然后把纸片展平.第二步,如图②.把这个正方形折成两个相等的矩形,再把纸片展平.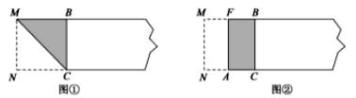
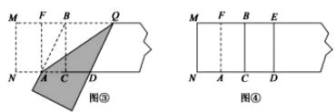 第三步,折出内侧矩形的对角线 AB,并把 AB折到图③中所示的AD处,第四步,展平纸片,按照所得的点D折出 DE,使 DE⊥ND,则图④中就会出现黄金矩形,问题解决: (1)图③中AB=________(保留根号); (2)如图③,判断四边形 BADQ的形状,并说明理由; (3)请写出图④中所有的黄金矩形,并选择其中一个说明理由. (4)结合图④.请在矩形 BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽. 参考答案 一、选择题(每小题3分,共30分)1、C2、D3、D4、C5、B6、C7、D8、B9、B10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、
第三步,折出内侧矩形的对角线 AB,并把 AB折到图③中所示的AD处,第四步,展平纸片,按照所得的点D折出 DE,使 DE⊥ND,则图④中就会出现黄金矩形,问题解决: (1)图③中AB=________(保留根号); (2)如图③,判断四边形 BADQ的形状,并说明理由; (3)请写出图④中所有的黄金矩形,并选择其中一个说明理由. (4)结合图④.请在矩形 BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽. 参考答案 一、选择题(每小题3分,共30分)1、C2、D3、D4、C5、B6、C7、D8、B9、B10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、![]() 6 2
6 2![]() . 12、
. 12、![]() 13、504m214、<15、x<116、﹣2(答案不唯一) 三、解下列各题(本大题共8小题,共72分)17、见解析18、 (1) 八(1)班的优秀率为
13、504m214、<15、x<116、﹣2(答案不唯一) 三、解下列各题(本大题共8小题,共72分)17、见解析18、 (1) 八(1)班的优秀率为![]() ,八(2)班的优秀率为
,八(2)班的优秀率为![]() 八(1)、八(2)班的中位数分别为150,147;(2)八(1)班获冠军奖19、 (1) y=10x+3000(x≥0,且x为整数);(2) 110件产品;(3) 超过150件.20、(1)四边形ABCD的面积=14
八(1)、八(2)班的中位数分别为150,147;(2)八(1)班获冠军奖19、 (1) y=10x+3000(x≥0,且x为整数);(2) 110件产品;(3) 超过150件.20、(1)四边形ABCD的面积=14![]() ;(2)是.理由见解析.21、(1)y=20―3x;(2)三种方案,即: 方案一:甲种3辆 乙种11辆 丙种6辆 方案二:甲种4辆 乙种8辆 丙种8辆 方案三:甲种5辆 乙种5辆 丙种10辆 (3)方案一,即甲种3辆,乙种11辆,丙种6辆,最大利润为16.44万元。22、(1)
;(2)是.理由见解析.21、(1)y=20―3x;(2)三种方案,即: 方案一:甲种3辆 乙种11辆 丙种6辆 方案二:甲种4辆 乙种8辆 丙种8辆 方案三:甲种5辆 乙种5辆 丙种10辆 (3)方案一,即甲种3辆,乙种11辆,丙种6辆,最大利润为16.44万元。22、(1)![]() ;(2)
;(2)![]() ;(3)在
;(3)在![]() 轴上存在点
轴上存在点![]()
![]()
![]() 使
使![]() 为等腰三角形23、(1)见解析;(2)8;(3)80分24、(1)
为等腰三角形23、(1)见解析;(2)8;(3)80分24、(1)![]() ;(2)见解析;(3) 见解析; (4) 见解析.
;(2)见解析;(3) 见解析; (4) 见解析.
相关试卷
这是一份贵州省贵阳市名校2023-2024学年八上数学期末质量跟踪监视试题含答案,共8页。
这是一份重庆市涪陵区名校2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔,下列点在直线上的是等内容,欢迎下载使用。
这是一份贵州省安顺市名校2022-2023学年数学七下期末质量跟踪监视模拟试题含答案,共6页。试卷主要包含了二次根式中字母a的取值范围是,y=,下列运算正确的是,下列各式中,运算正确的是等内容,欢迎下载使用。








