


辽宁省新宾县联考2022-2023学年数学七下期末考试试题含答案
展开这是一份辽宁省新宾县联考2022-2023学年数学七下期末考试试题含答案,共7页。
辽宁省新宾县联考2022-2023学年数学七下期末考试试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.
4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.
5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在下列命题中,是假命题的个数有( )
①如果![]() ,那么
,那么![]() . ② 两条直线被第三条直线所截,同位角相等
. ② 两条直线被第三条直线所截,同位角相等
③面积相等的两个三角形全等 ④ 三角形的一个外角等于不相邻的两个内角的和.
A.3个 B.2个 C.1个 D.0个
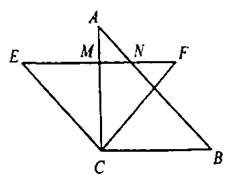
2.把两个全等的等腰直角三角形如图放置在一起![]() ,点
,点![]() 关于
关于![]() 对称
对称![]() 交
交![]() ,
,![]() 于点
于点![]() ,则
,则![]() 与
与![]() 的面积比为( )
的面积比为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
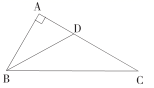
3.如图,![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() 交
交![]() 于
于![]() ,若
,若![]() ,则
,则![]() 的面积为( )
的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.下列函数中,是一次函数的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.如图,△ABC是等边三角形,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为12,则PD+PE+PF=( )
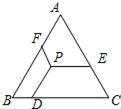
A.12 B.8 C.4 D.3
6.以下列各组数为边长,不能构成直角三角形的是( )
A.5,12,13 B.1,2,![]() C.1,
C.1,![]() ,2 D.4,5,6
,2 D.4,5,6
7.学校举行演讲比赛,共有15名同学进入决赛,比赛将评出金奖1名,银奖3名,铜奖4名,某选手知道自己的分数后,要判断自己能否获奖,他应当关注有关成绩的( )
A.平均数 B.中位数 C.众数 D.方差
8.如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=26°,则∠OBC的度数为( )
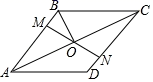
A.54° B.64° C.74° D.26°
9.在端午节到来之前,儿童福利院对全体小朋友爱吃哪几种粽子作调查,以决定最终买哪种粽子.下面的调查数据中最值得关注的是( )
A.方差 B.平均数 C.中位数 D.众数
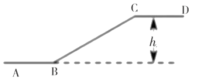
10.如图,是某超市一楼与二楼之间的阶梯式电梯示意图,其中![]() 、
、![]() 分别表示一楼、二楼地面的水平线,
分别表示一楼、二楼地面的水平线,![]() ,
,![]() 的长为
的长为![]() , 则乘电梯从点
, 则乘电梯从点![]() 到点
到点![]() 上升的高度
上升的高度![]() 是( )
是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 外一点,连接
外一点,连接![]() 、
、![]() 、
、![]() ,且
,且![]() 交
交![]() 于点
于点![]() ,在
,在![]() 上取一点
上取一点![]() ,使得
,使得![]() ,
,![]() .若
.若![]() ,则
,则![]() 的度数为
的度数为![]()
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
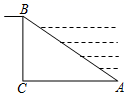
12.河堤横断面如图所示,斜坡AB的坡度=1:![]() ,BC=5米,则AC的长是( )米.
,BC=5米,则AC的长是( )米.
A.![]() B.5 C.15 D.
B.5 C.15 D.![]()
二、填空题(每题4分,满分20分,将答案填在答题纸上)
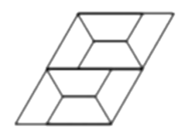
13.如图,是用形状、大小完全相同的等腰梯形密铺成的图案,则这个图案中的等腰梯形的底角(指钝角)是___________度.(温馨提示:等腰梯形是一组对边平行,且同一底边上两底角相等的四边形)
14.已知![]() 、
、![]() 、
、![]() 是反比例函数
是反比例函数![]() 的图象上的三点,且
的图象上的三点,且![]() ,则
,则![]() 、
、![]() 、
、![]() 的大小关系是________________.
的大小关系是________________.
15.如图,在平面直角坐标系中,点P(﹣1,2)关于直线x=1的对称点的坐标为_____.
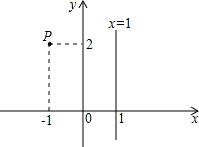
16.如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为__.
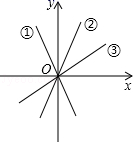
17.如图,三个正比例函数的图象分别对应表达式:①y=ax,②y=bx,③y=cx,将a,b,c从小到大排列并用“<”连接为_____.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)阅读下列题目的解题过程:
已知a、b、c为△ABC的三边,且满足a2c2﹣b2c2=a4﹣b4,试判断△ABC的形状.
解:∵a2c2﹣b2c2=a4﹣b4 (A)
∴c2(a2﹣b2)=(a2+b2)(a2﹣b2) (B)
∴c2=a2+b2 (C)
∴△ABC是直角三角形
问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号: ;
(2)错误的原因为: ;
(3)本题正确的结论为: .
19.(5分)张明、王成两位同学在初二学年10次数学单元检测的成绩(成绩均为整数,且个位数为0)如图所示利用图中提供的信息,解答下列问题:
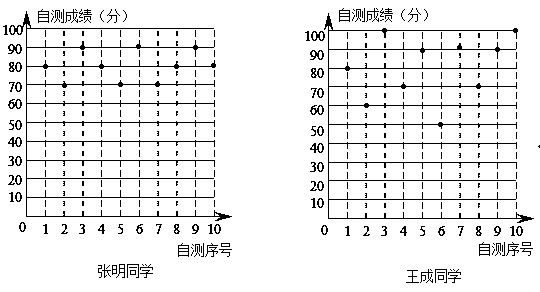
(1)完成下表:
姓名 | 平均成绩 | 中位数 | 众数 | 方差(s2) |
张明 |
| 80 | 80 |
|
王成 |
|
|
| 260 |
(2)如果将90分以上(含90分)的成绩视为优秀,则优秀率较高的同学是 ;
(3)根据图表信息,请你对这两位同学各提出学习建议.
20.(8分) “金牛绿道行“活动需要租用![]() 、
、![]() 两种型号的展台,经前期市场调查发现,用
两种型号的展台,经前期市场调查发现,用![]() 元租用的
元租用的![]() 型展台的数量与用
型展台的数量与用![]() 元租用的
元租用的![]() 型展台的数量相同,且每个
型展台的数量相同,且每个![]() 型展台的价格比每个
型展台的价格比每个![]() 型展台的价格少
型展台的价格少![]() 元.
元.
(1)求每个![]() 型展台、每个
型展台、每个![]() 型展台的租用价格分别为多少元(列方程解应用题);
型展台的租用价格分别为多少元(列方程解应用题);
(2)现预计投入资金至多![]() 元,根据场地需求估计,
元,根据场地需求估计,![]() 型展台必须比
型展台必须比![]() 型展台多
型展台多![]() 个,问
个,问![]() 型展台最多可租用多少个.
型展台最多可租用多少个.
21.(10分)解方程:x2﹣2x=1.
22.(10分)已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)求证:无论![]() 取何实数,该方程总有两个不相等的实数根;
取何实数,该方程总有两个不相等的实数根;
(2)若方程的一根为3,求另一个根.
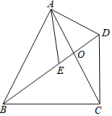
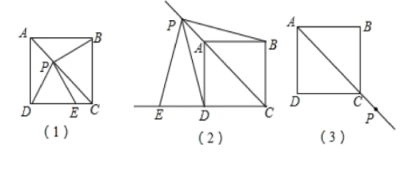
23.(12分)已知正方形ABCD,点P是对角线AC所在直线上的动点,点E在DC边所在直线上,且随着点P的运动而运动,PE=PD总成立。
(1)如图(1),当点P在对角线AC上时,请你通过测量、观察,猜想PE与PB有怎样的关系?(直接写出结论不必证明);
(2)如图(2),当点P运动到CA的延长线上时,(1)中猜想的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由;
(3)如图(3),当点P运动到CA的反向延长线上时,请你利用图(3)画出满足条件的图形,并判断此时PE与PB有怎样的关系?(直接写出结论不必证明)
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、A
2、D
3、A
4、D
5、C
6、D
7、B
8、B
9、D
10、C
11、C
12、A
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、1
14、y2<y1<y3
15、(3,2)
16、![]()
17、a<c<b
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)C;(2)没有考虑a=b的情况;(3)△ABC是等腰三角形或直角三角形.
19、(1)张明:平均成绩80,方,60;王成:平均成绩80,中位,85,众,90;(2)王成;(3)张明学习成绩还需提高,优秀率有待提高.
20、(1)每个A型展台,每个B型展台的租用价格分别为800元、1200元;(2)B型展台最多可租用31个.
21、![]() ,
,![]() .
.
22、(1)见解析;(2)-1.
23、(1)①PE=PB,②PE⊥PB;(2)成立,理由见解析(3)①PE=PB,②PE⊥PB.
相关试卷
这是一份辽宁省新宾县联考2023-2024学年数学九年级第一学期期末达标测试试题含答案,共7页。试卷主要包含了二次函数的图象的顶点坐标是,如图,正方形的边长为,点在边上,方程的解是等内容,欢迎下载使用。
这是一份辽宁省新宾县2023-2024学年数学八上期末综合测试模拟试题含答案,共7页。试卷主要包含了已知,则M等于,在中,无理数的个数是等内容,欢迎下载使用。
这是一份2023-2024学年辽宁省新宾县联考数学八年级第一学期期末复习检测试题含答案,共8页。试卷主要包含了下面的计算中,正确的是等内容,欢迎下载使用。












