


重庆市涪陵区名校2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案
展开
这是一份重庆市涪陵区名校2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔,下列点在直线上的是等内容,欢迎下载使用。
重庆市涪陵区名校2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。2.答题时请按要求用笔。3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。 一、选择题(每小题3分,共30分)1.反比例函数 y=(2m-1)![]() ,当 x>0 时,y 随 x 的增大而增大,则 m 的值是( )A.m=±1 B.小于
,当 x>0 时,y 随 x 的增大而增大,则 m 的值是( )A.m=±1 B.小于![]() 的实数 C.-1 D.12.下列说法错误的是( )A.“买一张彩票中大奖”是随机事件B.不可能事件和必然事件都是确定事件C.“穿十条马路连遇十次红灯”是不可能事件D.“太阳东升西落”是必然事件3.如果不等式(a+1)x<a+1的解集为x>1,那么a的取值范围是( )A.a<1 B.a<﹣1 C.a>1 D.a>﹣14.已知一次函数
的实数 C.-1 D.12.下列说法错误的是( )A.“买一张彩票中大奖”是随机事件B.不可能事件和必然事件都是确定事件C.“穿十条马路连遇十次红灯”是不可能事件D.“太阳东升西落”是必然事件3.如果不等式(a+1)x<a+1的解集为x>1,那么a的取值范围是( )A.a<1 B.a<﹣1 C.a>1 D.a>﹣14.已知一次函数![]() ,且
,且![]() 随
随![]() 的增大而减小,那么它的图象经过A.第一、二、三象限 B.第一、二、四象限C.第一、三、四象限 D.第二、三、四象限5.如图,在
的增大而减小,那么它的图象经过A.第一、二、三象限 B.第一、二、四象限C.第一、三、四象限 D.第二、三、四象限5.如图,在![]() 中,
中,![]() 度.以
度.以![]() 的三边为边分别向外作等边三角形
的三边为边分别向外作等边三角形![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() 的面积分别是8和3,则
的面积分别是8和3,则![]() 的面积是( )
的面积是( )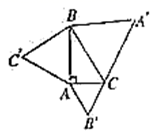 A.
A.![]() B.
B.![]() C.
C.![]() D.56.下列图书馆的标志中,是中心对称图形的是( )A.
D.56.下列图书馆的标志中,是中心对称图形的是( )A. B.
B. C.
C. D.
D. 7.下列各式中,能用公式法分解因式的是( )①
7.下列各式中,能用公式法分解因式的是( )①![]() ; ②
; ②![]() ; ③
; ③![]() ; ④
; ④![]() ; ⑤
; ⑤![]() A.2个 B.3个 C.4个 D.5个8.下列点在直线
A.2个 B.3个 C.4个 D.5个8.下列点在直线![]() 上的是( )A.
上的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 9.如图,将边长为10的正三角形OAB放置于平面直角坐标系xOy中,C是AB边上的动点(不与端点A,B重合),作CD⊥OB于点D,若点C,D都在双曲线y=
9.如图,将边长为10的正三角形OAB放置于平面直角坐标系xOy中,C是AB边上的动点(不与端点A,B重合),作CD⊥OB于点D,若点C,D都在双曲线y=![]() 上(k>0,x>0),则k的值为( )
上(k>0,x>0),则k的值为( )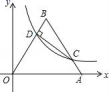 A.25
A.25![]() B.18
B.18![]() C.9 D.9
C.9 D.9![]() 10.数据1、5、7、4、8的中位数是
10.数据1、5、7、4、8的中位数是![]()
![]() A.4 B.5 C.6 D.7二、填空题(本大题共有6小题,每小题3分,共18分)11.已知点
A.4 B.5 C.6 D.7二、填空题(本大题共有6小题,每小题3分,共18分)11.已知点![]() ,
,![]() 关于x轴对称,则
关于x轴对称,则![]() ________.12.正方形网格中,∠AOB如图放置,则tan∠AOB=______________.
________.12.正方形网格中,∠AOB如图放置,则tan∠AOB=______________.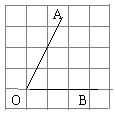 13.一组数据2,x,4,6,7,已知这组数据的众数是6,那么这组数据的方差是________.14.已知点(-4,y1),(2,y2)都在直线y=ax+2(a<0)上,则y1, y2的大小关系为_________ .15.如图,Rt△
13.一组数据2,x,4,6,7,已知这组数据的众数是6,那么这组数据的方差是________.14.已知点(-4,y1),(2,y2)都在直线y=ax+2(a<0)上,则y1, y2的大小关系为_________ .15.如图,Rt△![]() 中,
中,![]() 分别是
分别是![]() 的中点,
的中点,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() .若
.若![]() ,
,![]() ,则
,则![]() 的长是________.
的长是________.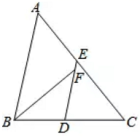 16.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E. F分别是AO、AD的中点,若AC=8,则EF=___.
16.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E. F分别是AO、AD的中点,若AC=8,则EF=___.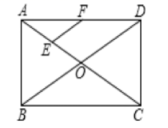 三、解下列各题(本大题共8小题,共72分)17.(8分)自
三、解下列各题(本大题共8小题,共72分)17.(8分)自![]() 年
年![]() 月
月![]() 日
日![]() 日起,合肥市进入冰雪灾害天气,如图,一棵大树在离地面
日起,合肥市进入冰雪灾害天气,如图,一棵大树在离地面![]() 米处折断,树的顶端落在离树干底部
米处折断,树的顶端落在离树干底部![]() 米处,求这棵树折断之前的高度.
米处,求这棵树折断之前的高度.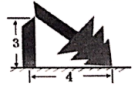 18.(8分)计算化简(1)
18.(8分)计算化简(1)![]() (2)
(2)![]() 19.(8分)在平面直角坐标系中,过点C(1,3)、D(3,1)分别作x轴的垂线,垂足分别为A、B.(1)求直线CD和直线OD的解析式;(2)点M为直线OD上的一个动点,过M作x轴的垂线交直线CD于点N,是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;(3)若△AOC沿CD方向平移(点C在线段CD上,且不与点D重合),在平移的过程中,设平移距离为
19.(8分)在平面直角坐标系中,过点C(1,3)、D(3,1)分别作x轴的垂线,垂足分别为A、B.(1)求直线CD和直线OD的解析式;(2)点M为直线OD上的一个动点,过M作x轴的垂线交直线CD于点N,是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;(3)若△AOC沿CD方向平移(点C在线段CD上,且不与点D重合),在平移的过程中,设平移距离为![]() t,△AOC与△OBD重叠部分的面积记为s,试求s与t的函数关系式.
t,△AOC与△OBD重叠部分的面积记为s,试求s与t的函数关系式.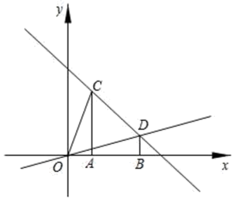 20.(8分)去年3月,某炒房团以不多于2224万元不少于2152万元的资金分别从A城、B城买入小户型二手房(80平方米/套)共4000平方米.其中A城、B城的购入价格分别为4000元/平方米、7000元/平方米.自住建部今年5月约谈成都市政府负责同志后,成都市进一步加大了调控政策.某炒房团为抛售A城的二手房,决定从6月起每平方米降价1000元.如果卖出相同平方米的房子,那么5月的销售额为640万元,6月的销售额为560万元.(1)A城今年6月每平方米的售价为多少元?(2)请问去年3月有几种购入方案?(3)若去年三月所购房产全部没有卖出,炒房团计划在7月执行销售方案:B城售价为1.05万元/平方米,并且每售出一套返还该购房者a元;A城按今年6月的价格进行销售。要使(2)中的所有方案利润相同,求出a应取何值? 21.(8分)某厂为支援灾区人民,要在规定时间内加工1500顶帐篷.在加工了300顶帐篷后,厂家把工作效率提高到原来的1.5倍,结果提前4天完成任务,求该厂原来每天加工多少顶帐篷? 22.(10分)码头工人每天往一艘轮船上装载货物,平均每天装载速度y(吨/元)与装完货物所需时间x(天)之间是反比例函数关系,其图象如图所示.(1)求这个反比例函数的表达式;(2)由于紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸货多少吨?(3)若码头原有工人10名,且每名工人每天的装卸量相同,装载完毕恰好用了8天时间,在(2)的条件下,至少需要增加多少名工人才能完成任务?
20.(8分)去年3月,某炒房团以不多于2224万元不少于2152万元的资金分别从A城、B城买入小户型二手房(80平方米/套)共4000平方米.其中A城、B城的购入价格分别为4000元/平方米、7000元/平方米.自住建部今年5月约谈成都市政府负责同志后,成都市进一步加大了调控政策.某炒房团为抛售A城的二手房,决定从6月起每平方米降价1000元.如果卖出相同平方米的房子,那么5月的销售额为640万元,6月的销售额为560万元.(1)A城今年6月每平方米的售价为多少元?(2)请问去年3月有几种购入方案?(3)若去年三月所购房产全部没有卖出,炒房团计划在7月执行销售方案:B城售价为1.05万元/平方米,并且每售出一套返还该购房者a元;A城按今年6月的价格进行销售。要使(2)中的所有方案利润相同,求出a应取何值? 21.(8分)某厂为支援灾区人民,要在规定时间内加工1500顶帐篷.在加工了300顶帐篷后,厂家把工作效率提高到原来的1.5倍,结果提前4天完成任务,求该厂原来每天加工多少顶帐篷? 22.(10分)码头工人每天往一艘轮船上装载货物,平均每天装载速度y(吨/元)与装完货物所需时间x(天)之间是反比例函数关系,其图象如图所示.(1)求这个反比例函数的表达式;(2)由于紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸货多少吨?(3)若码头原有工人10名,且每名工人每天的装卸量相同,装载完毕恰好用了8天时间,在(2)的条件下,至少需要增加多少名工人才能完成任务?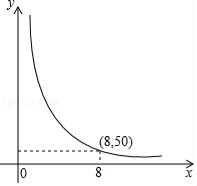 23.(10分)如图,在
23.(10分)如图,在![]() 中,点
中,点![]() ,
,![]() 是直线
是直线![]() 上的两点,
上的两点,![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,
,![]() .
.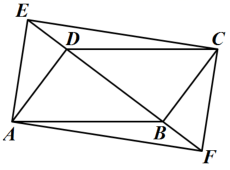 (1)求证:四边形
(1)求证:四边形![]() 是平行四边形.(2)若
是平行四边形.(2)若![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 是矩形,求
是矩形,求![]() 的长. 24.(12分)类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.(1)概念理解在“平行四边形、菱形、矩形、正方形”中是“等邻边四边形”的是 .(2)概念应用在Rt△ABC中,∠C=
的长. 24.(12分)类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.(1)概念理解在“平行四边形、菱形、矩形、正方形”中是“等邻边四边形”的是 .(2)概念应用在Rt△ABC中,∠C=![]() ,AB=5,AC=3.点D是AB边的中点,点E是BC边上的一个动点,若四边形ADEC是“等邻边四边形”,则CE= .
,AB=5,AC=3.点D是AB边的中点,点E是BC边上的一个动点,若四边形ADEC是“等邻边四边形”,则CE= . 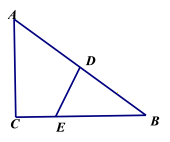 参考答案 一、选择题(每小题3分,共30分)1、C2、C3、B4、B5、D6、C7、B8、C9、D10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、
参考答案 一、选择题(每小题3分,共30分)1、C2、C3、B4、B5、D6、C7、B8、C9、D10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、![]() 12、113、3.114、y1>y215、1;16、2 三、解下列各题(本大题共8小题,共72分)17、
12、113、3.114、y1>y215、1;16、2 三、解下列各题(本大题共8小题,共72分)17、![]() 米18、(1)
米18、(1)![]() (2)
(2)![]() 19、(1)直线OD的解析式为y=
19、(1)直线OD的解析式为y=![]() x;(2)存在.满足条件的点M的横坐标
x;(2)存在.满足条件的点M的横坐标![]() 或
或![]() ,理由见解析;(3)S=﹣
,理由见解析;(3)S=﹣![]() (t﹣1)2+
(t﹣1)2+![]() .20、(1)A城今年6月每平方米的售价为
.20、(1)A城今年6月每平方米的售价为![]() 元;(2)方案有四种,如表所示见解析;(3)
元;(2)方案有四种,如表所示见解析;(3)![]() 应取40000元.21、原来每天加工100顶帐篷. 22、(1)
应取40000元.21、原来每天加工100顶帐篷. 22、(1)![]() ;(2) 80吨货物;(3)6名.23、 (1)见解析;(2)
;(2) 80吨货物;(3)6名.23、 (1)见解析;(2)![]() 24、(1)菱形,正方形;(2)CE=3或
24、(1)菱形,正方形;(2)CE=3或![]()
相关试卷
这是一份2023-2024学年重庆市涪陵区名校八上数学期末教学质量检测模拟试题含答案,共6页。试卷主要包含了下列等式成立的是,使分式有意义的x的取值范围是等内容,欢迎下载使用。
这是一份贵州省毕节地区名校2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,五边形的内角和为,已知,则化简的结果是等内容,欢迎下载使用。
这是一份广西省桂林市名校2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,用配方法解方程,则方程可变形为,下列函数中,是反比例函数的为,下列图形是轴对称的是等内容,欢迎下载使用。









