重庆市梁平区2022-2023学年数学七年级第二学期期末质量检测模拟试题含答案

重庆市梁平区2022-2023学年数学七年级第二学期期末质量检测模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。

2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。答案不能答在试题卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按以上要求作答无效。

4．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。

一、选择题(每小题3分,共30分)

1．已知△ABC的三边之长分别为a、1、3，则化简|9-2a|-的结果是（　　）

A．12-4a B．4a-12 C．12 D．-12

2．若在实数范围内有意义，则x的取值范围是（　　）

A．x＞-4 B．x≥-4 C．x＞-4且x≠1 D．x≥-4且x≠-1

3．多项式2m+4与多项式m2+4m+4的公因式是(　　)

A．m+2 B．m﹣2 C．m+4 D．m﹣4

4．尺规作图要求：Ⅰ、过直线外一点作这条直线的垂线；Ⅱ、作线段的垂直平分线；

Ⅲ、过直线上一点作这条直线的垂线；Ⅳ、作角的平分线．

如图是按上述要求排乱顺序的尺规作图：

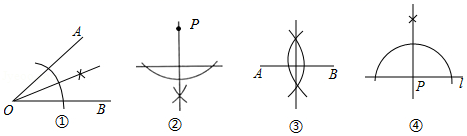
则正确的配对是（　　）

A．①﹣Ⅳ，②﹣Ⅱ，③﹣Ⅰ，④﹣Ⅲ B．①﹣Ⅳ，②﹣Ⅲ，③﹣Ⅱ，④﹣Ⅰ

C．①﹣Ⅱ，②﹣Ⅳ，③﹣Ⅲ，④﹣Ⅰ D．①﹣Ⅳ，②﹣Ⅰ，③﹣Ⅱ，④﹣Ⅲ

5．计算()2的结果是(　　)

A．－2 B．2 C．±2 D．4

6．关于函数y=，下列结论正确的是（　　）

A．函数图象必经过点（1，4）

B．函数图象经过二三四象限

C．y随x的增大而增大

D．y随x的增大而减小

7．下列计算或化简正确的是（　　）

A． B．

C． D．

8．如图，在平行四边形ABCD中，∠B＝60°，将△ABC沿对角线AC折叠，点B的对应点落在点E处，且点B，A，E在一条直线上，CE交AD于点F，则图中等边三角形共有(   )

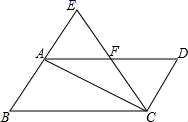
A．4个 B．3个 C．2个 D．1个

9．下列算式中，正确的是　　

A． B．

C． D．

10．下列属于矩形具有而菱形不具有的性质是（　　）

A．两组对边分别平行且相等

B．两组对角分别相等

C．对角线相互平分

D．四个角都相等

二、填空题(本大题共有6小题，每小题3分，共18分)

11．《九章算术》中记载：今有户不知高、广，竿不知长、短，横之不出四尺，纵之不出二尺，邪之适出．问户高、广、邪各几何？这段话翻译后是：今有门，不知其高、宽，有竿，不知其长、短．横放，竿比门宽长出4尺；竖放，竿比门高长出2尺；斜放，竿与门对角线恰好相等．问门高、宽、对角线长分别是多少？若设门对角线长为x尺，则可列方程为_____．

12．苏州市2017年6月份最后六大的最高气温分别为31，34，36，27，25，33（单位：℃）．这组数据的极差是_____．

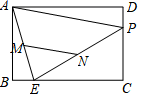
13．如图，矩形ABCD中，AB=6，BC=8，E是BC上一点（不与B、C重合），点P在边CD上运动，M、N分别是AE、PE的中点，线段MN长度的最大值是_____．

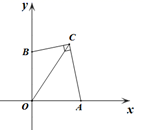
14．如图，在平面直角坐标系xOy中，A,B两点分别在x轴，y轴的正半轴上，且OA=OB，点C在第一象限，OC=3，连接BC，AC，若∠BCA=90°，则BC+AC的值为_________．

15．若，，则=___________.

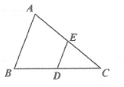
16．如图，在△ABC中，点D，E分别是BC，AC的中点，AB=8，则DE的长为________.

三、解下列各题(本大题共8小题，共72分)

17．（8分）阅读下面的材料:

 解方程，这是一个一元四次方程，根据该方程的特点，

它的解法通常采用换元法降次:设，那么，于是原方程可变为

，解得.当时，，∴；当时，

，∴；

原方程有四个根: .

仿照上述换元法解下列方程:

 (1)                           

 (2) .

18．（8分）如图，在平面直角坐标系中，矩形OABC的顶点A在y轴的正半轴上，点C在x轴的正半轴上，线段OA,OC的长分别是m，n且满足(m-6)2+＝0，点D是线段OC上一点，将△AOD沿直线AD翻折，点O落在矩形对角线AC上的点E处

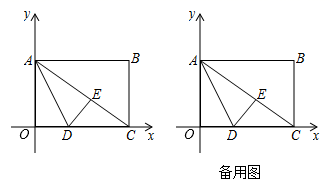
（1）求线段OD的长

（2）求点E的坐标

（3）DE所在直线与AB相交于点M，点N在x轴的正半轴上，以M、A、N、C为顶点的四边形是平行四边形时，求N点坐

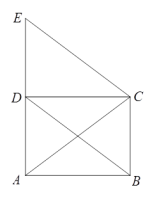
19．（8分）已知：如图，四边形ABCD是平行四边形，CE∥BD交AD的延长线于点E，CE=AC．

（1）求证：四边形ABCD是矩形；

（2）若AB=4，AD=3，求四边形BCED的周长．

20．（8分）某书店老板去图书批发市场购买某种图书，第一次用500元购书若干本，很快售完由于该书畅销，第二次购书时，每本书的批发价已比第一次提高了20%，他用900元所购该书的数量比第一次的数量多了10本．

（1）求第一次购书每本多少元？

（2）如果这两次所购图书的售价相同，且全部售完后总利润不低于25%，那么每本图书的售价至少是多少元？

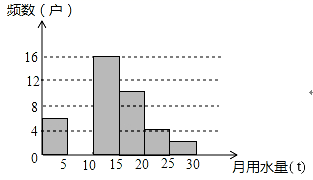
21．（8分）八年级（1）班同学为了解某小区家庭月均用水情况，随机调査了该小区部分家庭，并将调查数据整理成如下两幅不完整的统计图表：

请根据以上信息，解答以下问题：

（1）直接写出频数分布表中的m、n的值并把频数直方图补充完整；

（2）求出该班调查的家庭总户数是多少？

（3）求该小区用水量不超过15的家庭的频率．

22．（10分）已知：如图，平面直角坐标系中，，，点C是x轴上一点，点D为OC的中点．

（1）求证：BD∥AC；

（2）若点C在x轴正半轴上，且BD与AC的距离等于2，求点C的坐标；

（3）如果于点E，当四边形ABDE为平行四边形时，求直线AC的解析式．

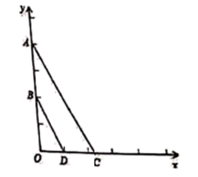
23．（10分） (1)计算：﹣×

(2)解方程：x2﹣4x﹣5＝0

24．（12分）如图，在平面直角坐标系中，直线与坐标轴交于，过线段的中点作的垂线，交轴于点．

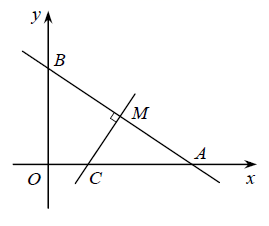
（1）填空：线段，，的数量关系是______________________；

（2）求直线的解析式．

参考答案

一、选择题(每小题3分,共30分)

1、A

2、D

3、A

4、D

5、B

6、C

7、D

8、B

9、C

10、D

二、填空题(本大题共有6小题，每小题3分，共18分)

11、x1＝（x﹣4）1+（x﹣1）1

12、32

13、5

14、

15、

16、1

三、解下列各题(本大题共8小题，共72分)

17、（1）；（2），为原方程的解

18、（1）OD=3；（2）E点（，）（3）点N为（，0）或（，0）

19、（1）详见解析；（2）1.

20、（1）第一次购书每本25元；（2）每本图书的售价至少是1元．

21、（1）m=12,n=0.08;（2）50；（3）0.68.

22、（1）BD∥AC；（2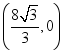）；（3）

23、（1）；（2）x＝﹣1或x＝1．

24、（1）；（2）