重庆市南川区部分学校2022-2023学年七年级数学第二学期期末复习检测模拟试题含答案

这是一份重庆市南川区部分学校2022-2023学年七年级数学第二学期期末复习检测模拟试题含答案，共7页。试卷主要包含了下列式子变形是因式分解的是，分式方程＝有增根，则增根为等内容，欢迎下载使用。
重庆市南川区部分学校2022-2023学年七年级数学第二学期期末复习检测模拟试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 考生须知：1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。 一、选择题(每小题3分,共30分)1．下列图形中，既是轴对称图形又是中心对称图形的有（   ）A．4个 B．3个 C．2个 D．1个2．在式子，，，，，中，分式的个数有（    ）A．2 B．3 C．4 D．53．ABCD是一块正方形场地，小华和小萌在AB上取一点E，测量得，，这块场地的对角线长是( 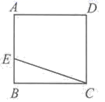    )A．10 B．30 C．40 D．504．若a+c=b，那么方程ax2+bx+c=0（a≠0）必有一根是（　　）A．1    B．﹣1    C．±1    D．05．如图，在平面直角坐标系中，半径均为1个单位长度的半圆O1，O2，O3…组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒个单位长度，则第2017秒时点P的坐标是(　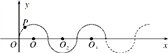　)A．(2016，0) B．(2017，1) C．(2017，－1) D．(2018，0)6．下列式子变形是因式分解的是(　　)A．x2－2x－3＝x(x－2)－3B．x2－2x－3＝(x－1)2－4C．(x＋1)(x－3)＝x2－2x－3D．x2－2x－3＝(x＋1)(x－3)7．如图，在四边形ABCD中，AD∥BC，∠BCD＝90°，将四边形ABCD沿AB方向平移得到四边形A'B'C'D'，BC与C'D'相交于点E，若BC＝8，CE＝3，C'E＝2，则阴影部分的面积为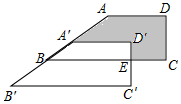（　　）A．12+2 B．13 C．2+6 D．268．在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如表所示：成绩/米1.501.601.651.701.751.80人数232341则这15运动员的成绩的众数和中位数分别为（　　）A．1.75，1.70 B．1.75，1.65 C．1.80，1.70 D．1.80，1.659．下列哪组条件能够判定四边形 ABCD 是平行四边形？（    ）A．AB // CD ， AD  BC B．AB  CD ， AD  BCC．A  B ， C  D D．AB  AD ， CB  CD10．分式方程＝有增根，则增根为（　　）A．0 B．1 C．1或0 D．﹣5二、填空题(本大题共有6小题，每小题3分，共18分)11．如图，两个反比例函数y＝ 和y＝ 在第一象限内的图象依次是C2和C1，设点P在C1上，PC⊥x轴于点C，交C2于点A，PD⊥y轴于点D，交C2于点B，则四边形PAOB的面积为_________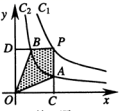．12．如图，正方形中，点在上，交、于点、，点、分别为、的中点，连接、，若，，则______.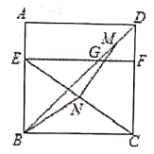13．一项工程，甲单独做x小时完成，乙单独做y小时完成，则两人一起完成这项工程需要___小时．14．如图，在正方形ABCD中，H为AD上一点，∠ABH＝∠DBH，BH交AC于点G．若HD＝2，则线段AD的长为_____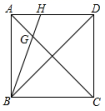．15．方程＝0的解是___．16．当a__________时，分式有意义．三、解下列各题(本大题共8小题，共72分)17．（8分）某智能手机越来越受到大众的喜爱，各种款式相继投放市场，某店经营的A款手机去年销售总额为50000元，今年每部销售价比去年降低400元，若卖出的数量相同，销售总额将比去年减少20%．已知A，B两款手机的进货和销售价格如下表： A款手机B款手机进货价格（元）11001400销售价格（元）今年的销售价格2000（1）今年A款手机每部售价多少元？（2）该店计划新进一批A款手机和B款手机共90部，且B款手机的进货数量不超过A款手机数量的两倍，应如何进货才能使这批手机获利最多？   18．（8分）如图，在平面直角坐标系中，A9m,0、Bm,0m0，以AB为直径的⊙M交y轴正半轴于点C，CD是⊙M的切线，交x轴正半轴于点D，过A作AECD于E，交⊙于F.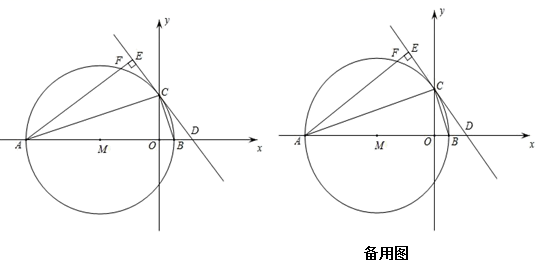（1）求C的坐标；（用含m的式子表示）（2）①请证明：EFOB；②用含m的式子表示AFC的周长；（3）若，，分别表示的面积，记，对于经过原点的二次函数，当时，函数y的最大值为a，求此二次函数的解析式.   19．（8分）如图，在ABCD中，点E，F分别在AD，BC边上，且BE∥DF.求证:(1)四边形BFDE是平行四边形； (2)AE=CF.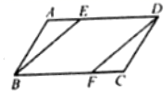   20．（8分）先分解因式，再求值：，其中，．   21．（8分）如图，在Rt△BAC中，∠BAC=90°，将△ABC绕点A顺时针旋转90°得到△AB′C′（点B的对应点是点B′，点C的对应点是点C′），连接CC′，若∠CC′B′=30°，求∠B的度数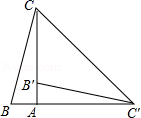．   22．（10分）一商店销售某种商品，平均每天可售出20件，每件盈利40元.为了扩大销售、增加盈利，该店采取了降价措施，在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件.（1）若降价3元，则平均每天销售数量为________件；    （2）当每件商品降价多少元时，该商店每天销售利润为1200元？   23．（10分）如图，在△ABC中，BD、CE分别为AC、AB边上的中线，BD、CE交于点H，点G、F分别为HC、HB的中点，连接AH、DE、EF、FG、GD，其中HA＝BC．（1）证明：四边形DEFG为菱形；（2）猜想当AC、AB满足怎样的数量关系时，四边形DEFG为正方形，并说明理由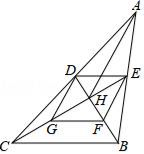．   24．（12分）在矩形ABCD中，点E、F分别在AB，BC上，△DEF为等腰直角三角形，∠DEF=90°，AD+CD=10，AE=2，求AD的长. 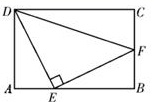  参考答案 一、选择题(每小题3分,共30分)1、C2、B3、C4、B5、B6、D7、B8、A9、B10、B 二、填空题(本大题共有6小题，每小题3分，共18分)11、212、13、14、15、x＝5.16、 三、解下列各题(本大题共8小题，共72分)17、（1）今年A款手机每部售价1600元；（2）当新进A款手机30部，B款手机60部时，这批手机获利最大．18、（1）C(0,3m)；（2）①证明见解析；②8m+；(3) 或19、（1）见解析；（2）见解析.20、，121、75°．22、（1）26；（2）每件商品降价2元时，该商店每天销售利润为12元.23、（1）证明见解析；（2）当AC＝AB时，四边形DEFG为正方形，证明见解析24、AD=2.