


贵州省仁怀市2022-2023学年数学七年级第二学期期末学业水平测试试题含答案
展开
这是一份贵州省仁怀市2022-2023学年数学七年级第二学期期末学业水平测试试题含答案,共8页。试卷主要包含了一次函数的图象不经过的象限是等内容,欢迎下载使用。
贵州省仁怀市2022-2023学年数学七年级第二学期期末学业水平测试试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。 一、选择题(每小题3分,共30分)1.某班5位学生参加中考体育测试的成绩(单位:分)分别是:50、45、36、48、50,则这组数据的众数是( )A.36 B.45 C.48 D.502.某快递公司快递员张海六月第三周投放快递物品件数为:有1天是41件,有2天是35件,有4天是37件,这周里张海日平均投递物品件数为( )A.36件 B.37件 C.38件 D.38.5件3.一次函数![]() 的图象不经过的象限是( )A.第一象限 B.第二象限C.第三象限 D.第四象限4.如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是( )
的图象不经过的象限是( )A.第一象限 B.第二象限C.第三象限 D.第四象限4.如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是( )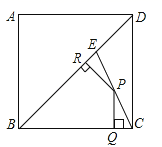 A.2
A.2![]() B.2 C.2
B.2 C.2![]() D.
D.![]() 5.下列各图象中,( )表示y是x的一次函数.A.
5.下列各图象中,( )表示y是x的一次函数.A.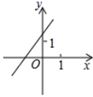 B.
B.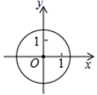 C.
C.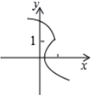 D.
D.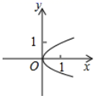 6.下列关于反比例函数
6.下列关于反比例函数![]() 的说法中,错误的是()A.图象经过点
的说法中,错误的是()A.图象经过点![]() B.当
B.当![]() 时,
时,![]() C.两支图象分别在第二、四象限 D.两支图象关于原点对称7.如图,已知四边形ABCD是平行四边形,下列结论中错误的是( )
C.两支图象分别在第二、四象限 D.两支图象关于原点对称7.如图,已知四边形ABCD是平行四边形,下列结论中错误的是( )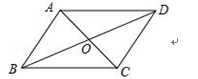 A.当AB=BC时,它是菱形 B.当AC⊥BD时,它是菱形C.当AC=BD时,它是矩形 D.当∠ABC=90°时,它是正方形8.如图,在
A.当AB=BC时,它是菱形 B.当AC⊥BD时,它是菱形C.当AC=BD时,它是矩形 D.当∠ABC=90°时,它是正方形8.如图,在![]() 中,
中,![]() =55°,
=55°,![]() ,分别以点
,分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径画弧,两弧相交于点
的长为半径画弧,两弧相交于点![]() ,作直线
,作直线![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() 的度数为( )
的度数为( )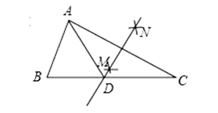 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 9.在矩形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
9.在矩形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )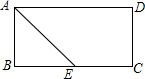 A.2和3 B.3和2 C.4和1 D.1和410.菱形的对角线长分别是
A.2和3 B.3和2 C.4和1 D.1和410.菱形的对角线长分别是![]() ,则这个菱形的面积是( )A.
,则这个菱形的面积是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,函数
二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,函数![]() 和
和![]() 的图象相交于点A(
的图象相交于点A(![]() ,3),则不等式
,3),则不等式![]() 的解集为___________.
的解集为___________.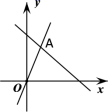 12.如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是 .
12.如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是 .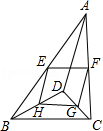 13.如图,菱形ABCD中,点O为对角线AC的三等分点且AO=2OC,连接OB,OD,OB=OC=OD,已知AC=3,那么菱形的边长为_____.
13.如图,菱形ABCD中,点O为对角线AC的三等分点且AO=2OC,连接OB,OD,OB=OC=OD,已知AC=3,那么菱形的边长为_____.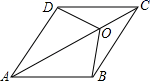 14.如图,
14.如图,![]() ABCD的顶点
ABCD的顶点![]() 在矩形
在矩形![]() 的边
的边![]() 上,点
上,点![]() 与点
与点![]() 不重合,若
不重合,若![]() 的面积为4,则图中阴影部分两个三角形的面积和为_________.
的面积为4,则图中阴影部分两个三角形的面积和为_________.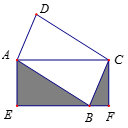 15.如图,已知矩形ABCD,AB在y轴上,AB=2,BC=3,点A的坐标为(0,1),在AD边上有一点E(2,1),过点E的直线与BC交于点F.若EF平分矩形ABCD的面积,则直线EF的解析式为________.
15.如图,已知矩形ABCD,AB在y轴上,AB=2,BC=3,点A的坐标为(0,1),在AD边上有一点E(2,1),过点E的直线与BC交于点F.若EF平分矩形ABCD的面积,则直线EF的解析式为________. 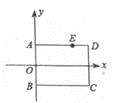 16.平面直角坐标系xOy中,直线y=11x﹣12与x轴交点坐标为_____.三、解下列各题(本大题共8小题,共72分)17.(8分)如图1,P是菱形ABCD对角线AC上的一点,点E在BC的延长线上,且PE=PB(1)求证:PD=PE;(2)求证:∠DPE=∠ABC;(3)如图2,当四边形ABCD为正方形时,连接DE,试探究线段DE与线段BP的数量关系,并说明理由.
16.平面直角坐标系xOy中,直线y=11x﹣12与x轴交点坐标为_____.三、解下列各题(本大题共8小题,共72分)17.(8分)如图1,P是菱形ABCD对角线AC上的一点,点E在BC的延长线上,且PE=PB(1)求证:PD=PE;(2)求证:∠DPE=∠ABC;(3)如图2,当四边形ABCD为正方形时,连接DE,试探究线段DE与线段BP的数量关系,并说明理由.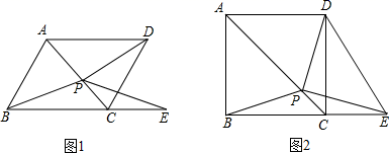 18.(8分)八年级(3)班同学为了解2020年某小区家庭1月份天然气使用情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:月均用气量x(
18.(8分)八年级(3)班同学为了解2020年某小区家庭1月份天然气使用情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:月均用气量x(![]() )频数(户)频率0<x≤1040.0810<x≤20a0.1220<x≤30160.3230<x≤4012b40<x≤50100.2050<x≤6020.04
)频数(户)频率0<x≤1040.0810<x≤20a0.1220<x≤30160.3230<x≤4012b40<x≤50100.2050<x≤6020.04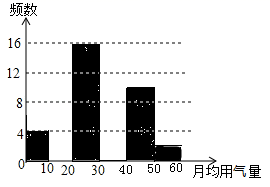 (1)求出a,b的值,并把频数分布直方图补充完整;(2)求月均用气量不超过30
(1)求出a,b的值,并把频数分布直方图补充完整;(2)求月均用气量不超过30![]() 的家庭数占被调查家庭总数的百分比;(3)若该小区有600户家庭,根据调查数据估计,该小区月均用气量超过40
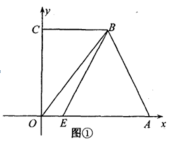
的家庭数占被调查家庭总数的百分比;(3)若该小区有600户家庭,根据调查数据估计,该小区月均用气量超过40![]() 的家庭大约有多少户? 19.(8分)如图①,将直角梯形
的家庭大约有多少户? 19.(8分)如图①,将直角梯形![]() 放在平面直角坐标系中,已知
放在平面直角坐标系中,已知![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,连结
,连结![]() .
.
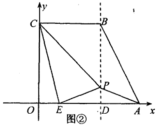 (1)求证:
(1)求证:![]() ;(2)如图②,过点
;(2)如图②,过点![]() 作
作![]() 轴于
轴于![]() ,点
,点![]() 在直线
在直线![]() 上运动,连结
上运动,连结![]() 和
和![]() .①当
.①当![]() 的周长最短时,求点
的周长最短时,求点![]() 的坐标;②如果点
的坐标;②如果点![]() 在
在![]() 轴上方,且满足
轴上方,且满足![]() ,求
,求![]() 的长. 20.(8分)如图,已知
的长. 20.(8分)如图,已知![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() 、
、![]() 、
、![]() .
.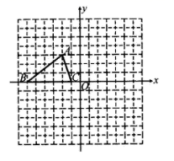 (1)请直接写出点
(1)请直接写出点![]() 关于原点对称的点的坐标;(2)将
关于原点对称的点的坐标;(2)将![]() 绕坐标原点
绕坐标原点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,画出
,画出![]() ,直接写出点
,直接写出点![]() 、
、![]() 的对应点的点
的对应点的点![]() 、
、![]() 坐标;(3)请直接写出:以
坐标;(3)请直接写出:以![]() 、
、![]() 、
、![]() 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点![]() 的坐标. 21.(8分)在平面直角坐标系中,原点为O,已知一次函数的图象过点A(0,5),点B(﹣1,4)和点P(m,n)(1)求这个一次函数的解析式;(2)当n=2时,求直线AB,直线OP与x轴围成的图形的面积;(3)当△OAP的面积等于△OAB的面积的2倍时,求n的值 22.(10分)如图,正方形ABCD中,AB=4,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED,交AB于点F,以DE、EF为邻边作矩形DEFG,连接AG.(1)求证:矩形DEFG是正方形;(2)求AG+AE的值;(3)若F恰为AB中点,连接DF交AC于点M,请直接写出ME的长.
的坐标. 21.(8分)在平面直角坐标系中,原点为O,已知一次函数的图象过点A(0,5),点B(﹣1,4)和点P(m,n)(1)求这个一次函数的解析式;(2)当n=2时,求直线AB,直线OP与x轴围成的图形的面积;(3)当△OAP的面积等于△OAB的面积的2倍时,求n的值 22.(10分)如图,正方形ABCD中,AB=4,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED,交AB于点F,以DE、EF为邻边作矩形DEFG,连接AG.(1)求证:矩形DEFG是正方形;(2)求AG+AE的值;(3)若F恰为AB中点,连接DF交AC于点M,请直接写出ME的长. 23.(10分)某中学开学初到商场购买
23.(10分)某中学开学初到商场购买![]() 、
、![]() 两种品牌的足球,购买
两种品牌的足球,购买![]() 种品牌的足球50个,
种品牌的足球50个,![]() 种品牌的足球25个,共花费4500元,已知购买一个
种品牌的足球25个,共花费4500元,已知购买一个![]() 种品牌的足球比购买一个
种品牌的足球比购买一个![]() 种品牌的足球少30元.(1)求购买一个
种品牌的足球少30元.(1)求购买一个![]() 种品牌、一个
种品牌、一个![]() 种品牌的足球各需多少钱.(2)学校为了响应“足球进校园”的号召,决定再次购进
种品牌的足球各需多少钱.(2)学校为了响应“足球进校园”的号召,决定再次购进![]() 、
、![]() 两种品牌足球共50个,正好赶上商场对商品价格进行调整,
两种品牌足球共50个,正好赶上商场对商品价格进行调整,![]() 品牌的足球售价上涨4元,
品牌的足球售价上涨4元,![]() 品牌足球按原售价的9折出售,如果学校第二次购买足球的总费用不超过第一次花费的
品牌足球按原售价的9折出售,如果学校第二次购买足球的总费用不超过第一次花费的![]() ,且保证
,且保证![]() 品牌足球不少于23个,则学校有几种购买方案?(3)求出学校在第二次购买活动中最多需要多少钱? 24.(12分)已知:如图,点B,C,D在同一直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H,(1)求证:△BCE≌△ACD;(2)求证:CF=CH;(3)判断△CFH的形状并说明理由.
品牌足球不少于23个,则学校有几种购买方案?(3)求出学校在第二次购买活动中最多需要多少钱? 24.(12分)已知:如图,点B,C,D在同一直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H,(1)求证:△BCE≌△ACD;(2)求证:CF=CH;(3)判断△CFH的形状并说明理由.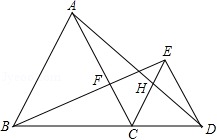 参考答案 一、选择题(每小题3分,共30分)1、D2、B3、A4、A5、A6、C7、D8、A9、B10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、x≥1.512、1.13、
参考答案 一、选择题(每小题3分,共30分)1、D2、B3、A4、A5、A6、C7、D8、A9、B10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、x≥1.512、1.13、![]() .14、115、y=2x-3.16、 (
.14、115、y=2x-3.16、 (![]() ,0). 三、解下列各题(本大题共8小题,共72分)17、(1)详见解析;(2)详见解析;(3)DE=
,0). 三、解下列各题(本大题共8小题,共72分)17、(1)详见解析;(2)详见解析;(3)DE=![]() BP,理由详见解析18、(1)6,
BP,理由详见解析18、(1)6,![]() ,图见解析;(2)
,图见解析;(2)![]() ;(3)1.19、(1)见解析;(2)①
;(3)1.19、(1)见解析;(2)①![]() ;②
;②![]() 或820、 (1)
或820、 (1) ![]() ;(2)图详见解析,
;(2)图详见解析,![]() ,
,![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() 21、(1)y=x+5;(2)5;(1)7或122、(1)见解析;(2)AE+AG==4
21、(1)y=x+5;(2)5;(1)7或122、(1)见解析;(2)AE+AG==4![]() ;(3)EM=
;(3)EM=![]() .23、(1)购买一个A种品牌的足球需要50元,购买一个B种品牌的足球需要80元;(2)有三种方案,详见解析;(3)最多需要3150元.24、(1)证明见解析;(2)证明见解析;(3)△CFH是等边三角形,理由见解析.
.23、(1)购买一个A种品牌的足球需要50元,购买一个B种品牌的足球需要80元;(2)有三种方案,详见解析;(3)最多需要3150元.24、(1)证明见解析;(2)证明见解析;(3)△CFH是等边三角形,理由见解析.
相关试卷
这是一份贵州省威宁县2023-2024学年八上数学期末学业水平测试试题含答案,共7页。试卷主要包含了如图,C为线段AE上一动点,下列几个数中,属于无理数的数是,下列计算正确的是等内容,欢迎下载使用。
这是一份贵州省遵义市桐梓达兴中学2022-2023学年数学七年级第二学期期末学业水平测试模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
这是一份贵州省水城实验学校2022-2023学年数学七年级第二学期期末学业水平测试试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。









