重庆綦江区2022-2023学年数学七年级第二学期期末学业水平测试模拟试题含答案

重庆綦江区2022-2023学年数学七年级第二学期期末学业水平测试模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

考生请注意：

1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。

2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。

3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。

一、选择题(每小题3分,共30分)

1．如图，在平面直角坐标系中，菱形ABCD的顶点A、B的坐标分别为（3，0）、（-2，0），点D在y轴正半轴上，则点C的坐标为（     ）

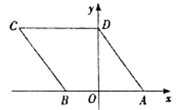
A．（-3，4）． B．（-4，3）． C．（-5，3）． D．（-5，4）．

2．某中学制作了108件艺术品，现用A、B两种不同的包装箱进行包装，已知每个B型包装箱比A型包装箱多装5件艺术品，单独使用B型包装箱比单独使用A型包装箱可少用2个．设B型包装箱每个可以装x件艺术品，根据题意列方程为（　　）

A． B．

C． D．

3．教练要从甲、乙两名射击运动员中选一名成绩较稳定的运动员参加比赛．两人在形同条件下各打了5发子弹，命中环数如下：甲：9、8、7、7、9；乙：10、8、9、7、1．应该选（ ）参加．

A．甲 B．乙 C．甲、乙都可以 D．无法确定

4．某跳远队准备从甲、乙、丙、丁4名运动员中选取成绩好且稳定的一名选手参赛，经测试，他们的成绩如下表，综合分析应选(   )

A．甲 B．乙 C．丙 D．丁

5．正方形具有而菱形不具有的性质是（   ）

A．四边相等 B．对角线相等

C．两组对边分别平行 D．一条对角线平分一组对角

6．下列点在直线y=-x+1上的是        （   ）

A．（2，-1） B．（3，3） C．（4，1） D．（1，2）

7．已知两条对角线长分别为和的菱形，顺次连接它的四边的中点得到的四边形的面积是 （  ）

A．100 B．48 C．24 D．12

8．有下列说法：①平行四边形既是中心对称图形，又是轴对称图形；②正方形有四条对称轴；③平行四边形相邻两个内角的和等于；④菱形的面积计算公式，除了“底×高”之外，还有“两对角线之积”；⑤矩形和菱形均是特殊的平行四边形，因此具有平行四边形的所有性质.其中正确的结论的个数有（    ）

A．1 B．2 C．3 D．4

9．如图，将含30°角的直角三角板ABC的直角顶点C放在直尺的一边上，已知∠A＝30°，∠1＝40°，则∠2的度数为(    )

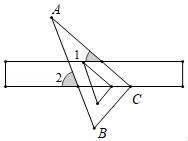
A．55° B．60° C．65° D．70°

10．如果，那么下列各式正确的是（　　）

A．a+5＜b+5 B．5a＜5b C．a﹣5＜b﹣5 D．

二、填空题(本大题共有6小题，每小题3分，共18分)

11．已知关于的方程的一个根是x=－1，则_______．

12．如图，C、D点在BE上，∠1=∠2，BD=EC，请补充一个条件：____________，使△ABC≌△FED．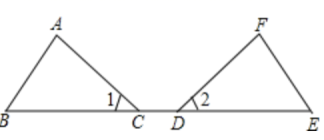

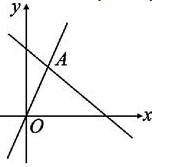
13．如图，函数y＝bx和y＝ax＋4的图象相交于点A（1，3），则不等式bx＜ax＋4的解集为________．

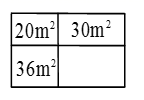
14．如图，一块矩形的土地被分成4小块，用来种植4种不同的花卉，其中3块面积分别是，，，则第四块土地的面积是____．

15．要使代数式有意义，则的取值范围是________．

16．如图，已知中，，，，是的垂直平分线，交于点，连接，则___

三、解下列各题(本大题共8小题，共72分)

17．（8分）已知2y+1与3x-3成正比例，且x=10时，y=4

（1）求y与x之间的函数关系式，并指出它是什么函数；（2）点P在这个函数图象上吗？

18．（8分）如图，直线的解析式为，与轴交于点，直线经过点（0，5），与直线交于点（﹣1，），且与轴交于点.       

（1）求点的坐标及直线的解析式；

（2）求△的面积．

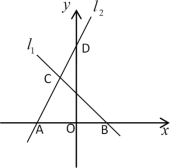
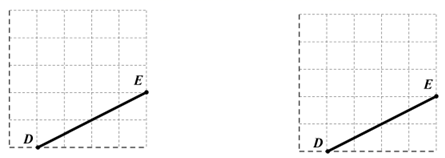
19．（8分）如图是由25个边长为1的小正方形组成的网格，请在图中画出以为斜边的2个面积不同的直角三角形.（要求：所画三角形顶点都在格点上）

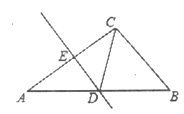
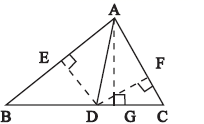
20．（8分）学完三角形的高后，小明对三角形与高线做了如下研究：如图，是中边上的-点，过点、分别作、、、，垂足分别为点、、，由与的面积之和等于的面积，有等量关系式：.像这种利用同一平面图形的两种面积计算途径可以得出相关线段的数量关系式，从而用于解决数学问题的方法称为“等积法”，下面请尝试用这种方法解决下列问题.

                                        图(1)                          图(2)

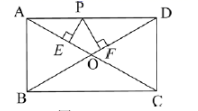
(1)如图(1)， 矩形中，，，点是上一点，过点作，，垂足分别为点、，求的值；

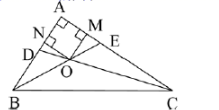
(2)如图(2)，在中，角平分线、相交于点，过点分别作、，垂足分别为点、，若，，求四边形的周长.

21．（8分）某校为了迎接体育中考，了解学生的体质情况，学校随机调查了本校九年级名学生“秒跳绳”的次数，并将调查所得的数据整理如下：

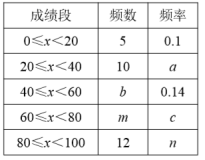
秒跳绳次数的频数、频率分布表

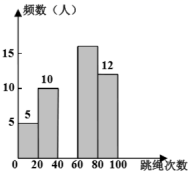
秒跳绳次数的频数分布直方图

、

根据以上信息，解答下列问题：

（1）表中，     ，       ；

（2）请把频数分布直方图补充完整；

（3）若该校九年级共有名学生，请你估计“秒跳绳”的次数以上（含次）的学生有多少人？

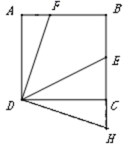
22．（10分）如图，正方形ABCD的边长为6，点E为BC的中点，点F在AB边上，，H在BC延长线上，且CH=AF，连接DF，DE，DH。

（1）求证DF=DH；

（2）求的度数并写出计算过程．

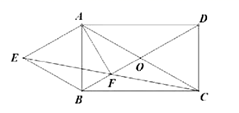
23．（10分）如图，矩形的对角线交于点，点是矩形外的一点，其中．

（1）求证：四边形是菱形；

（2）若，连接交于于点，连接，求证：平分．

24．（12分）如图，在正方形中，，点是边上的动点（含端点，），连结，以所在直线为对称轴作点的对称点，连结，，，，点，，分别是线段，，的中点，连结，．

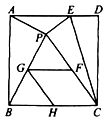
（1）求证：四边形是菱形；

（2）若四边形的面积为，求的长；

（3）以其中两边为邻边构造平行四边形，当所构造的平行四边形恰好是菱形时，这时该菱形的面积是________．

参考答案

一、选择题(每小题3分,共30分)

1、D

2、B

3、A

4、B

5、B

6、A

7、D

8、C

9、D

10、D

二、填空题(本大题共有6小题，每小题3分，共18分)

11、

12、AC=DF（或∠A=∠F或∠B=∠E）

13、x＜1

14、54

15、且

16、5

三、解下列各题(本大题共8小题，共72分)

17、（1），y是x的一次函数；（2）点不在这个函数的图象上．

18、（1）；（2） .

19、见解析

20、（1）；（2）4

21、（1）；；（2）详见解析；（3）336

22、（1）详见解析；（2），理由详见解析.

23、（1）见解析；（2）见解析.

24、（1）证明见解析；（2）；（3）或或．