湘教版八年级下册4.3 一次函数的图象当堂检测题

A[一次函数的图象和性质]

一、选择题

1.(2020嘉兴)一次函数y=2x-1的图象大致是 (　　)

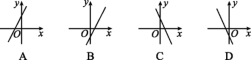
2.若ab<0且a>b,则函数y=ax+b的图象可能是 (　　)

3.直线y=2x-4与y轴的交点坐标是 (　　)

A.(4,0) B.(0,4) C.(-4,0) D.(0,-4)

4.(2020内江)将直线y=-2x-1向上平移2个单位,平移后的直线所对应的函数关系式为 (　　)

A.y=-2x-5 B.y=-2x-3 C.y=-2x+1 D.y=-2x+3

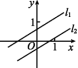
5.一次函数y1=k1x+b1的图象l1如图所示,将直线l1向下平移若干个单位后得到直线l2,l2的函数表达式为y2=k2x+b2.下列说法中错误的是(　　)

A.k1=k2 B.b1<b2 C.b1>b2 D.当x=5时,y1>y2

6.(2020镇江)一次函数y=kx+3(k≠0)的函数值y随x的增大而增大,则它的图象不经过 (　　)

A.第一象限 B.第二象限 C.第三象限 D.第四象限

7.一次函数y=mx+n与y=mnx(mn≠0)在同一平面直角坐标系中的图象可能是 (　　)

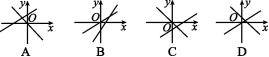
二、填空题

8.已知点M(1,a)和点N(2,b)是一次函数y=-2x+1的图象上的两点,则a与b的大小关系是　　　　. 

9.在一次函数y=(m-1)x+6中,y随x的增大而增大,则m的取值范围是　　　　. 

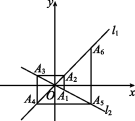
10.如图,在平面直角坐标系中,函数y=x和y=-x的图象分别为直线l1,l2,过点A11,-作x轴的垂线交l1于点A2,过点A2作y轴的垂线交l2于点A3,过点A3作x轴的垂线交l1于点A4,过点A4作y轴的垂线交l2于点A5……依次进行下去,则点A2022的横坐标为　　　　. 

三、解答题

11.在同一平面直角坐标系中,作出函数y=2x+3和y=2x的图象,并指出它们的位置关系.

12.已知一次函数y=(1-m)x+m-3.

(1)若一次函数的图象过原点,求实数m的值;

(2)当一次函数的图象经过第二、三、四象限时,求实数m的取值范围.

13.如图,已知直线AB的函数表达式为y=2x+10,与y轴交于点A,与x轴交于点B.

(1)直接写出点A,B的坐标;

(2)若P(a,b)为线段AB上的一个动点(不与点B重合),连接PO.若△PBO的面积为S,求S关于a的函数关系式.

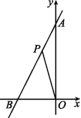
图

14.如图,在平面直角坐标系中,直线y=-x+3过点A(5,m)且与y轴交于点B,把点A向左平移2个单位,再向上平移4个单位,得到点C.过点C且与直线y=2x平行的直线交y轴于点D.

(1)求直线CD的函数表达式;

(2)直线AB与CD交于点E,将直线CD沿EB方向平移,平移到经过点B的位置结束,求直线CD在平移过程中与x轴交点横坐标的取值范围.

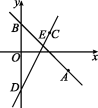
 [阅读理解与一题多变] 问题:探究一次函数y=kx+k+2(k是不为0的常数)图象的共性特点.

　　探究过程:小明尝试把x=-1代入,发现可以消去k,竟然求出了y=2.

老师问:结合一次函数的图象,这说明了什么?

小组讨论得出:无论k取何值,一次函数y=kx+k+2的图象一定经过点(-1,2).

老师:如果一次函数的图象是经过某一个定点的直线,那么我们把像这样的一次函数的图象定义为“点旋转直线”.

已知一次函数y=(k+3)x+(k-1)的图象是“点旋转直线”.

(1)一次函数y=(k+3)x+(k-1)的图象经过的定点P的坐标是　　　　; 

(2)已知一次函数y=(k+3)x+(k-1)的图象与x轴,y轴分别相交于点A,B.若△OBP的面积为3,求k的值.

答案

1.B

2. A　∵ab<0且a>b,∴a>0,b<0,

∴函数y=ax+b的图象经过第一、三、四象限.

3. D　与y轴的交点必在y轴上,而y轴上点的坐标特点是x=0,所以将x=0代入函数表达式中,得y=-4,所以直线与y轴的交点坐标为(0,-4).

4. C　原直线的k=-2,b=-1,向上平移2个单位得到了新直线,那么新直线的k=-2,b=-1+2=1,∴新直线所对应的函数关系式为y=-2x+1.因此本题选C.

5. B　∵将直线l1向下平移若干个单位后得到直线l2,

∴直线l1∥直线l2,

∴k1=k2.

∵直线l1向下平移若干个单位后得到直线l2,

∴b1>b2,

∴当x=5时,y1>y2.

6.D

7. C　(1)当m>0,n>0时,mn>0,

一次函数y=mx+n的图象经过第一、二、三象限,正比例函数y=mnx的图象经过第一、三象限,无符合选项;

(2)当m>0,n<0时,mn<0,

一次函数y=mx+n的图象经过第一、三、四象限,正比例函数y=mnx的图象经过第二、四象限,C选项符合;

(3)当m<0,n<0时,mn>0,

一次函数y=mx+n的图象经过第二、三、四象限,正比例函数y=mnx的图象经过第一、三象限,无符合选项;

(4)当m<0,n>0时,mn<0,

一次函数y=mx+n的图象经过第一、二、四象限,正比例函数y=mnx的图象经过第二、四象限,无符合选项.

故选C.

8.a>b

9. m>1

 ∵在一次函数y=(m-1)x+6中,y随x的增大而增大,

∴m-1>0,

解得m>1.

10. 21010

 观察发现规律:A11,-,A2(1,1),A3(-2,1),A4(-2,-2),A5(4,-2),A6(4,4),A7(-8,4),A8(-8,-8),…,

∴A2n的横坐标为(-2)n-1(n为正整数).

∵2022=2×1011,

∴点A2022的横坐标为(-2)1010=21010.

11.解:作图略.它们的位置关系是互相平行.

12.解:(1)∵一次函数y=(1-m)x+m-3的图象过原点,

∴

解得m=3.

(2)∵一次函数y=(1-m)x+m-3的图象经过第二、三、四象限,

∴

∴1<m<3.

13.解:(1)对于y=2x+10,

令x=0,得y=10;

令y=0,得x=-5,

则A(0,10),B(-5,0).

(2)∵P(a,b)在线段AB上,∴b=2a+10.

由(1)得OB=5,∴S△PBO=OB·(2a+10),

即S=×5(2a+10)=5a+25(-5<a≤0).

14.解:(1)在y=-x+3中,当x=5时,y=-2,故A(5,-2).

∵把点A向左平移2个单位,再向上平移4个单位,得到点C,

∴C(3,2).

∵直线CD平行于直线y=2x,

∴可设直线CD的函数表达式为y=2x+b(b≠0),则2×3+b=2,解得b=-4,

∴直线CD的函数表达式为y=2x-4.

(2)易知点B(0,3).

在y=2x-4中,令y=0,得2x-4=0,

解得x=2.

由题意易知平移后所得直线的函数表达式为y=2x+3.

令y=0,得2x+3=0,

解得x=-,

∴直线CD在平移过程中与x轴交点横坐标的取值范围是-≤x≤2.

[素养提升]

解:(1)把一次函数y=(k+3)x+(k-1)整理为y=k(x+1)+3x-1的形式,

令x+1=0,得x=-1,

当x=-1时,y=-4,

∴P(-1,-4).故答案为(-1,-4).

(2)∵一次函数y=(k+3)x+(k-1)的图象与x轴,y轴分别相交于点A,B,

∴A,0,B(0,k-1),则OB=|k-1|.

∵△OBP的面积为3,点P到y轴的距离为1,

∴|k-1|×1=3,

解得k=7或k=-5,

故k的值为7或-5.