初中数学2.7 正方形练习

[正方形]

一、选择题

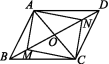
1.如图,已知四边形ABCD是正方形,对角线AC,BD相交于点O,则图中与△AOB全等的三角形有(　　)

A.1个 B.2个 C.3个 D.4个

2.(2020绵阳)如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴有              (　　)

A.2条 B.4条 C.6条 D.8条

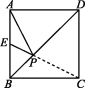
3.(2020滨州)下列命题是假命题的是 (　　)

A.对角线互相垂直且相等的平行四边形是正方形

B.对角线互相垂直的矩形是正方形

C.对角线相等的菱形是正方形

D.对角线互相垂直且平分的四边形是正方形

4.如图,在正方形ABCD中,点E,F分别在BC,CD上,BE=CF,则图中与∠AEB相等的角的个数是              (　　)

A.1 B.2 C.3 D.4

5.如图,F是正方形ABCD的边CD上的一个动点,BF的垂直平分线交对角线AC于点E,交BF于点M,连接BE,EF,则∠EBF的度数是              (　　)

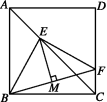
A.45° B.50° C.60° D.无法确定

二、填空题

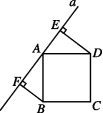
6.如图所示,直线a经过正方形ABCD的顶点A,分别过顶点D,B作DE⊥a于点E,BF⊥a于点F.若DE=4,BF=3,则EF的长为　　　　. 

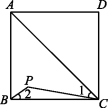
7.(2020镇江)如图,P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为　　　　. 

8.在平行四边形ABCD中,对角线AC与BD相交于点O,要使四边形ABCD是正方形,还需添加一组条件.下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD,其中符合题意的是　　　　　(填序号). 

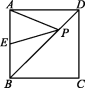
9.(2020毕节)如图,已知正方形ABCD的边长为4,E是边AB的中点,P是对角线BD上的动点,则AP+PE的最小值是　　　　. 

10.以正方形ABCD的边AD为一边作等边三角形ADE,则∠BEC的度数是　　　　. 

三、解答题

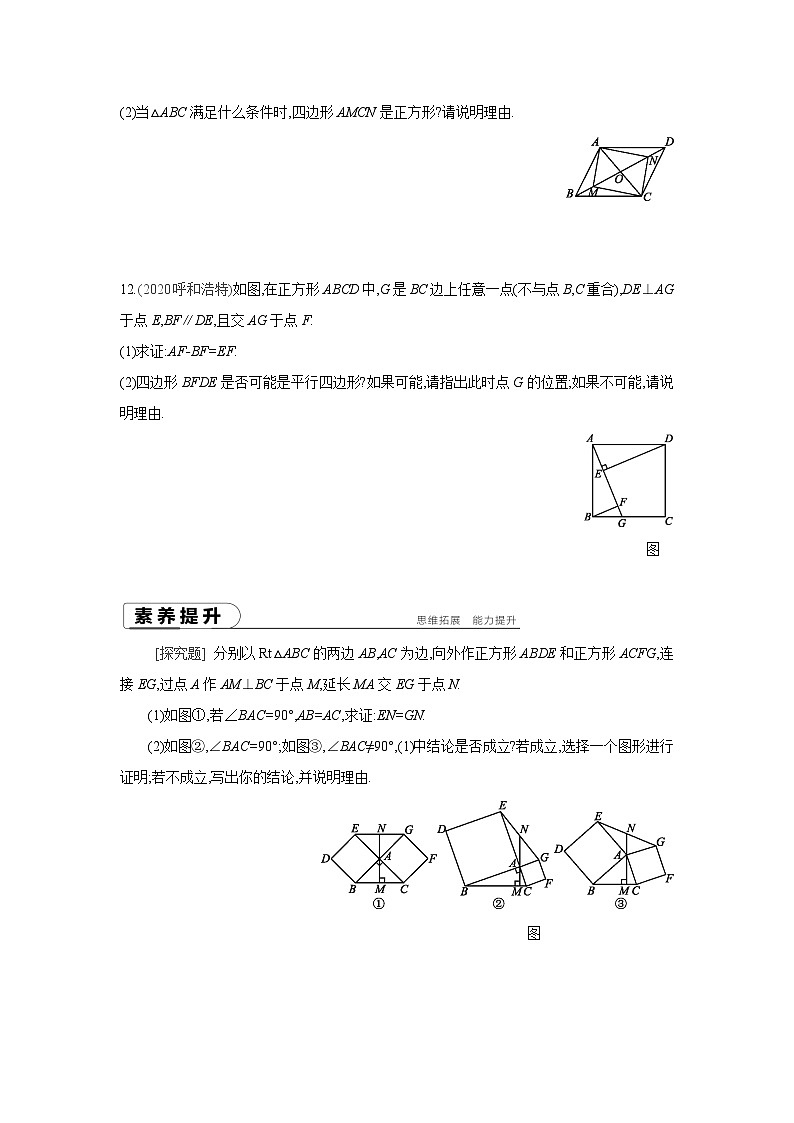
11.如图,已知平行四边形ABCD,若M,N是BD上两点,且BM=DN,AC=2OM.

(1)求证:四边形AMCN是矩形;

(2)当△ABC满足什么条件时,四边形AMCN是正方形?请说明理由.

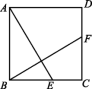
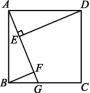
12.(2020呼和浩特)如图,在正方形ABCD中,G是BC边上任意一点(不与点B,C重合),DE⊥AG于点E,BF∥DE,且交AG于点F.

(1)求证:AF-BF=EF.

(2)四边形BFDE是否可能是平行四边形?如果可能,请指出此时点G的位置;如果不可能,请说明理由.

图 

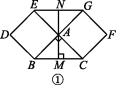
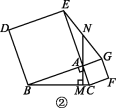
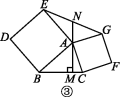
 [探究题] 分别以Rt△ABC的两边AB,AC为边,向外作正方形ABDE和正方形ACFG,连接EG,过点A作AM⊥BC于点M,延长MA交EG于点N.

(1)如图①,若∠BAC=90°,AB=AC,求证:EN=GN.

(2)如图②,∠BAC=90°;如图③,∠BAC≠90°,(1)中结论是否成立?若成立,选择一个图形进行证明;若不成立,写出你的结论,并说明理由.

图                  

答案

1. C　∵四边形ABCD是正方形,对角线AC,BD相交于点O,

∴OA=OB=OC=OD,AB=BC=CD=DA,

∴△AOB≌△BOC≌△COD≌△DOA,

∴与△AOB全等的三角形有3个.

2. B　如图.

故选B.

3. D　对角线互相垂直且平分的四边形是菱形,不一定是正方形.因此本题选D.

4. C　∵四边形ABCD是正方形,

∴AB∥CD,AD∥BC,AB=BC,∠ABE=∠BCF=90°.

在△ABE和△BCF中,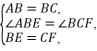

∴△ABE≌△BCF(SAS),

∴∠BFC=∠AEB.

∵AB∥CD,∴∠BFC=∠ABF,

∴∠ABF=∠AEB.

∵AD∥BC,∴∠AEB=∠DAE.

故图中与∠AEB相等的角的个数是3.

5. A　如图,过点E作EG⊥BC,EH⊥CD,垂足分别为G,H,易证明△BEG≌△FEH(HL),得∠BEG=∠FEH,所以∠BEF=∠GEH=90°,所以∠EBF=45°.故选A.

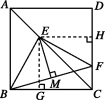
6. 7

 可证△ABF≌△DAE,则有AF=DE,AE=BF,故EF=AF+AE=DE+BF=4+3=7.

7. 135°

 ∵∠1=∠2,∴∠2+∠PCB=∠1+∠PCB=45°,∴∠P=135°.

8. ①③④

 ∵四边形ABCD是平行四边形,AB=AD,∴四边形ABCD是菱形.

又∵AB⊥AD,∴四边形ABCD是正方形,①正确;

由四边形ABCD是平行四边形,AB=BD,AB⊥BD,不能得到平行四边形ABCD是正方形,故②错误;

∵四边形ABCD是平行四边形,OB=OC,∴AC=BD,∴四边形ABCD是矩形.

又∵OB⊥OC,即对角线互相垂直,

∴平行四边形ABCD是正方形,③正确;

∵四边形ABCD是平行四边形,AB=AD,

∴四边形ABCD是菱形.

又∵AC=BD,∴四边形ABCD是正方形,

④正确.

9. 2

 ∵正方形ABCD的边长为4,E是边AB的中点,∴BE=2.∵P是对角线BD上的动点,连接PC,则PC=PA.连接EC交BD于点P,此时AP+PE=CP+PE=EC有最小值,最小值EC===2.故答案为2.

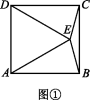
10. 30°或150°

 分两种情况:(1)如图①,等边三角形ADE在正方形ABCD的内部.∠CDE=∠CDA-∠ADE=90°-60°=30°.∵CD=DE,∴∠DCE=75°,∴∠ECB=90°-75°=15°,同理可以得到∠EBC=15°,

∴∠BEC=150°.

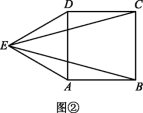
(2)如图②,等边三角形ADE在正方形ABCD的外部.∠CDE=∠CDA+∠ADE=90°+60°=150°.∵CD=DE,∴∠CED=15°.同理∠AEB=15°,∴∠BEC=∠AED-∠CED-∠AEB=60°-15°-15°=30°.

11.解:(1)证明:∵四边形ABCD是平行四边形,

∴OA=OC,OB=OD.

∵BM=DN,

∴OB-BM=OD-DN,即OM=ON,

∴四边形AMCN是平行四边形.

∵AC=2OM,∴MN=AC,

∴▱AMCN是矩形.

(2)当△ABC满足AB=BC时,四边形AMCN是正方形.

理由:∵AB=BC,OA=OC,

∴BO垂直平分AC.

∵点M在BO上,

∴AM=MC,∴矩形AMCN为正方形.

12.解:(1)证明:∵四边形ABCD是正方形,∴AB=AD,∠BAD=90°,∴∠BAF+∠DAE=90°.

∵DE⊥AG,∴∠AED=90°,

∴∠DAE+∠ADE=90°,∠DEF=90°,

∴∠ADE=∠BAF.

又∵BF∥DE,∴∠BFA=∠DEF=90°,

∴△ABF≌△DAE(AAS),∴AE=BF,

∴AF-BF=AF-AE=EF.

(2)不可能.理由:如图.

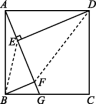
∵DE∥BF,∴当DE=BF时,四边形BFDE为平行四边形.

∵DE=AF,∴BF=AF,

即此时∠BAF=45°,而点G不与点B,C重合,

∴∠BAF≠45°,

∴四边形BFDE不可能是平行四边形.

[素养提升]

解:(1)证明:∵∠BAC=90°,AB=AC,

∴∠ACB=45°.

∵AM⊥BC,∴∠MAC=45°,

∴∠EAN=∠MAC=45°.

同理∠NAG=45°,∴∠EAN=∠NAG.

∵四边形ABDE和四边形ACFG为正方形,

∴EA=AB=AC=AG,∴EN=GN.

(2)如图①,当∠BAC=90°时,(1)中结论成立.

证明:过点E作EP⊥AN交AN的延长线于点P,过点G作GQ⊥AN于点Q.

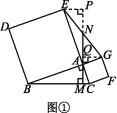
∵四边形ABDE是正方形,

∴AB=EA,∠BAE=90°,

∴∠EAP+∠BAM=180°-90°=90°.

∵AM⊥BC,∴∠ABM+∠BAM=90°,

∴∠ABM=∠EAP.

在△ABM和△EAP中,

∴△ABM≌△EAP(AAS),∴EP=AM.

同理可得GQ=AM,∴EP=GQ.

在△EPN和△GQN中,

∴△EPN≌△GQN(AAS),∴EN=GN.

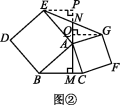
如图②,当∠BAC≠90°时,(1)中结论成立.

证明:过点E作EP⊥AN交AN的延长线于点P,过点G作GQ⊥AN于点Q.

∵四边形ABDE是正方形,

∴AB=EA,∠BAE=90°,

∴∠EAP+∠BAM=180°-90°=90°.

∵AM⊥BC,

∴∠ABM+∠BAM=90°,

∴∠ABM=∠EAP.

在△ABM和△EAP中,

∴△ABM≌△EAP(AAS),∴EP=AM.

同理可得GQ=AM,

∴EP=GQ.

在△EPN和△GQN中,

∴△EPN≌△GQN(AAS),

∴EN=GN.