湘教版八年级下册2.6.1菱形的性质一课一练

这是一份湘教版八年级下册2.6.1菱形的性质一课一练，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
[菱形的性质]一、选择题1.如图所示,在菱形ABCD中,AB=5,∠BAD=120°,则对角线AC的长是(　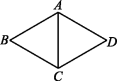　)A.20 B.15 C.10 D.52.(2020贵阳)菱形的两条对角线长分别是6和8,则此菱形的周长是 (　　)A.5 B.20 C.24 D.323.(2020甘孜州)如图,菱形ABCD中,对角线AC,BD相交于点O,E为AB的中点.若菱形ABCD的周长为32,则OE的长为   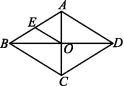           (　　)A.3 B.4 C.5 D.64.如图,在菱形ABCD中,M,N分别是边BC,CD上的点,且AM=AN=MN=AB,则∠C的度数为 (　　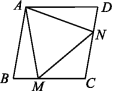)A.120° B.100° C.80° D.60°5.(2020遵义)如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为   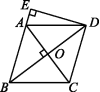           (　　)A. B. C.4 D.二、填空题6.(2020营口)如图,在菱形ABCD中,对角线AC,BD交于点O,其中OA=1,OB=2,则菱形ABCD的面积为　　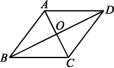　　. 7.(2020无锡)如图,在菱形ABCD中,∠B=50°,点E在CD上.若AE=AC,则∠BAE=　　　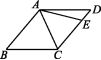　°. 8.如图,在菱形ABCD中,F是对角线AC上的一点,FE⊥AB于点E.若FE=3,则点F到AD的距离为　　　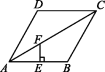　. 9.如图,在菱形ABCD中,对角线AC,BD的长分别为6,8,则图中阴影部分的面积为　　　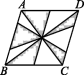　. 10.如图,在边长为2的菱形ABCD中,∠DAB=60°,E为AB的中点,F是AC上一动点,则EF+BF的最小值为　　　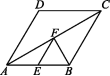　. 三、解答题11.(2020岳阳一模)如图,在菱形ABCD中,CE=CF.求证:AE=AF. 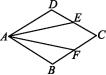 12.如图,在菱形ABCD中,E为对角线BD上一点,且AE=DE,连接CE.(1)求证:CE=DE;(2)当BE=4,CE=2时,求菱形ABCD的边长.   13.(2020北京)如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.(1)求证:四边形OEFG是矩形;(2)若AD=10,EF=4,求OE和BG的长.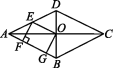    [分类讨论与动态几何问题] 如图,在菱形ABCD中,∠ABC=60°,BC=5 cm,点E从点A出发沿射线AD以1 cm/s的速度运动,同时点F从点B出发沿射线BC以2 cm/s的速度运动,设运动时间为t s.(1)连接EF,当EF经过BD的中点G时,求证:△DGE≌△BGF.(2)A,C,F,E四点能否组成平行四边形?若能,求出t的值;若不能,请说明理由.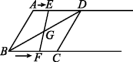图     
答案1.D2. B　如图所示: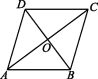∵四边形ABCD是菱形,AC=8,BD=6,∴AB=BC=CD=AD,OA=AC=4,OB=BD=3,AC⊥BD,∴AB===5,∴此菱形的周长=4×5=20.故选B.3. B　∵四边形ABCD是菱形,∴AB=BC=CD=DA,OA=OC.∵菱形ABCD的周长为32,∴BC=8.∵OA=OC,E为AB的中点,∴OE为△ABC的中位线,∴OE=BC=4.故选B.4. B　∵四边形ABCD是菱形,∴AB=AD.∵AM=AN=MN=AB,∴AB=AM,AN=AD,△AMN是等边三角形,∴∠B=∠AMB,∠D=∠AND,∠MAN=60°.设∠B=∠D=x,则∠BAM=∠DAN=180°-2x,∠BAD=2×(180°-2x)+60°=420°-4x.∵AB∥CD,∴∠BAD+∠D=180°,即(420°-4x)+x=180°,∴420°-3x=180°,解得x=80°,∴∠C=180°-80°=100°.5. D　在菱形ABCD中,∵AB=5,AO=AC=3,AC⊥BD,∴BO==4,∴BD=8,∴AB·DE=AC·BD,即5DE=×6×8,解得DE=.故选D.6. 4 根据菱形的对角线互相垂直且平分,得AC=2OA=2,BD=2OB=4,则S菱形ABCD=AC·BD=×2×4=4.7. 115 ∵四边形ABCD是菱形,∴AB=BC.又∵∠B=50°,∴∠BAC=∠BCA=65°.∵菱形ABCD关于直线AC对称,∴∠ACE=∠BCA=65°.又∵AC=AE,∴∠AEC=∠ACE=65°,∴在△ACE中,∠CAE=180°-∠ACE-∠AEC=50°,∴∠BAE=∠BAC+∠CAE=115°.8.39. 12 ∵对角线AC,BD的长分别为6,8,∴菱形ABCD的面积==24.∵菱形ABCD是中心对称图形,∴图中阴影部分的面积=×菱形ABCD的面积=12.故答案为12.10. 　 连接BD.点B,D关于AC对称,连接DE交AC于点F,则此时EF+BF的值最小,最小值是DE的长.依题意可知△ABD是等边三角形.∵E为AB的中点,∴DE⊥AB,∴DE===.11.证明:∵四边形ABCD为菱形,∴AD=AB=CD=CB,∠B=∠D.又∵CE=CF,∴CD-CE=CB-CF,即DE=BF.在△ADE和△ABF中,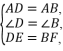∴△ADE≌△ABF(SAS),∴AE=AF.12.解:(1)证明:∵四边形ABCD是菱形,∴∠ABE=∠CBE,AB=CB.在△ABE和△CBE中,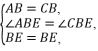∴△ABE≌△CBE(SAS),∴AE=CE.又∵AE=DE,∴CE=DE.(2)如图,连接AC交BD于点H.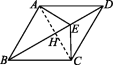∵四边形ABCD是菱形,∴AH⊥BD,BH=DH,AH=CH.∵CE=DE=AE=2,BE=4,∴BD=BE+DE=4+2=6,∴BH=BD=3,EH=BE-BH=1,∴CH===,∴BC===2,∴菱形ABCD的边长为2.13.解:(1)证明:∵四边形ABCD为菱形,∴O为BD的中点.∵E为AD的中点,∴OE为△ABD的中位线,∴OE∥FG.又∵OG∥EF,∴四边形OEFG为平行四边形.又∵EF⊥AB,∴▱OEFG为矩形.(2)∵E为AD的中点,AD=10,∴AE=AD=5.又∵∠EFA=90°,EF=4,∴在Rt△AEF中,AF===3.∵四边形ABCD为菱形,∴AB=AD=10,∴OE=AB=5.∵四边形OEFG为矩形,∴FG=OE=5,∴BG=AB-AF-FG=10-3-5=2.[素养提升]解:(1)证明:∵四边形ABCD是菱形,∴AD∥BC,∴∠EDG=∠FBG,∠DEG=∠BFG.∵G为BD的中点,∴DG=BG.在△DGE和△BGF中,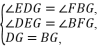∴△DGE≌△BGF(AAS).(2)能.①若点F在点C的左侧,根据题意,得AE=t cm,BF=2t cm,则CF=BC-BF=(5-2t)cm.∵AD∥BC,∴若AE=CF,则四边形AFCE是平行四边形,即t=5-2t,解得t=;②若点F在点C的右侧,根据题意,得AE=t cm,BF=2t cm,则CF=BF-BC=(2t-5)cm.∵AD∥BC,∴若AE=CF,则四边形ACFE是平行四边形,即t=2t-5,解得t=5.综上可得,当t=或t=5时,A,C,F,E四点能组成平行四边形.