初中数学湘教版八年级下册2.5.1矩形的性质课堂检测

[矩形的性质]

一、选择题

1.(2020南平期末)下列性质中,矩形具有但平行四边形不一定具有的是 (　　)

A.对边相等  B.对角相等

C.对角线相等  D.对角线互相平分

2.在矩形ABCD中,对角线AC,BD交于点O,以下说法错误的是 (　　)

A.∠ABC=90° B.AC=BD C.OA=OB D.OA=AD

3.如图,在矩形ABCD中,AC与BD交于点O.若AB=3,AC=6,则∠AOD的度数为 (　　)

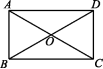
A.90° B.100° C.110° D.120°

4.(2020怀化)如图,在矩形ABCD中,AC,BD相交于点O,若△AOB的面积为2,则矩形ABCD的面积为              (　　)

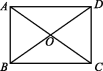
A.4 B.6 C.8 D.10

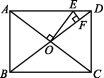
5.(2020广州)如图,矩形ABCD的对角线AC,BD交于点O,AB=6,BC=8,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+EF的值为              (　　)

A. B. C. D.

二、填空题

6.(2020青海)如图,在矩形ABCD中,对角线AC,BD相交于点O,已知∠BOC=120°,DC=3 cm,则AC的长为　　　　cm. 

7.如图,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F.若矩形ABCD的面积是12,则阴影部分的面积是　　　　. 

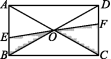
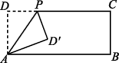
8.如图,在矩形纸片ABCD中,边AB=12,AD=5,P为DC边上的动点(点P不与点D,C重合),将纸片沿AP折叠,点D落在点D'处,则CD'的最小值为　　　　. 

三、解答题

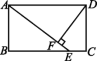
9.已知:如图,四边形ABCD是矩形(AD>AB),点E在BC上,且AE=AD,DF⊥AE,垂足为F.求证:DF=AB.

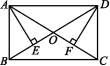
10.如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,DF⊥AC于点F.求证:AE=DF.

图   

11.如图,矩形ABCD的两条对角线AC,BD相交于点O,∠AOD=120°,AB=2.求矩形的边BC的长和矩形ABCD的面积.

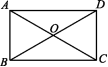
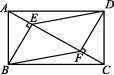
12.如图,在矩形ABCD中,E,F为BC上的两点,且BE=CF,连接AF,DE交于点O.

求证:(1)△ABF≌△DCE;

(2)△AOD是等腰三角形.

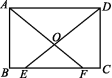
13.如图,在矩形ABCD中,BE⊥AC,DF⊥AC,垂足分别为E,F,连接DE,BF.

(1)求证:BE=DF;

(2)判断四边形BEDF的形状,并说明理由.

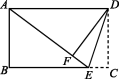
 [方程思想] 如图,在矩形ABCD中,E是BC边上的点,连接DE,AE,将△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.

(1)求证:△ABE≌△DFA;

(2)如果AB=6,EC∶BE=1∶4,求线段DE的长.

答案

1. C　矩形的性质有:四个角都是直角,对角线相等且互相平分,对边平行且相等;

平行四边形的性质有:对角相等,对边平行且相等,对角线互相平分;

故矩形具有但平行四边形不一定具有的性质是对角线相等.

故选C.

2.D　3.D

4. C　∵四边形ABCD是矩形,对角线AC,BD相交于点O,

∴AC=BD,且OA=OB=OC=OD,

∴S△ADO=S△BCO=S△CDO=S△AOB=2,

∴矩形ABCD的面积为4S△AOB=8.故选C.

5. C　∵四边形ABCD为矩形,∴∠ABC=90°,OA=OB=OC=OD.又∵AB=6,BC=8,∴AC=10,∴OA=OD=5.∵S△AOE+S△EOD=S△AOD=S矩形ABCD=×6×8=12,∴OA·OE+OD·EF=12,即×5OE+×5EF=12,∴OE+EF=.因此本题选C.

6. 6

 由矩形的性质可知∠ABC=90°,AB=DC=3 cm,OB=OC.

∵∠BOC=120°,

∴∠ACB=∠DBC=×(180°-120°)=30°,

∴AC=2AB=6 cm.

7. 3

 由矩形的中心对称性,得△AOE≌△COF,所以S△AOE=S△COF,所以S阴影=S△AOB=S矩形ABCD=3.

8. 8

 连接AC,当点D'在AC上时,CD'有最小值.

∵四边形ABCD是矩形,

∴∠D=∠B=90°,AD=BC.

∵AB=12,AD=5,∴BC=5,

∴AC===13.

由折叠的性质,得AD=AD'=5,

∴CD'的最小值=AC-AD'=13-5=8.

9.证明:∵四边形ABCD是矩形,DF⊥AE,

∴∠B=∠DFA=90°,AD∥BC,

∴∠DAF=∠AEB.

在△AFD和△EBA中,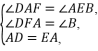

∴△AFD≌△EBA(AAS),

∴DF=AB.

10.证明:∵四边形ABCD是矩形,对角线AC,BD相交于点O,

∴OA=OC=OB=OD.

∵AE⊥BD,DF⊥AC,

∴∠AEO=∠DFO=90°.

在△AOE和△DOF中,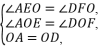

∴△AOE≌△DOF(AAS),∴AE=DF.

11.解:∵∠AOD=120°,

∴∠AOB=180°-120°=60°.

∵四边形ABCD是矩形,

∴∠ABC=90°,AC=BD,OA=OC=AC,OB=OD=BD,

∴OA=OB.

∵∠AOB=60°,∴△AOB是等边三角形,

∴OA=OB=AB=2,∴AC=2OA=4.

在直角三角形ABC中,BC===2,

则矩形ABCD的面积是AB·BC=2×2=4.

12. (1)先由BE=CF, 得BF=CE,

再根据矩形的性质得∠B=∠C=90°,AB=DC,

根据SAS可以判定△ABF≌△DCE;

(2)利用(1)中的△ABF≌△DCE,

可得∠BAF=∠CDE,

从而90°-∠BAF=90°-∠CDE,

即∠DAO=∠ADO,

所以OA=OD,

因此得△AOD是等腰三角形.

证明:(1)∵四边形ABCD为矩形,

∴AB=DC,∠B=∠C=90°.

∵BE=CF,∴BF=CE.

在△ABF和△DCE中,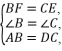

∴△ABF≌△DCE(SAS).

(2)由(1)知△ABF≌△DCE,

∴∠BAF=∠CDE.

∵∠DAF=90°-∠BAF,∠EDA=90°-∠CDE,

∴∠DAF=∠EDA,即∠DAO=∠ADO,

∴OA=OD,

∴△AOD是等腰三角形.

13.解:(1)证明:∵四边形ABCD是矩形,

∴AB∥CD,AB=CD,∴∠BAE=∠DCF.

∵BE⊥AC,DF⊥AC,

∴∠BEA=∠DFC=90°,

∴△ABE≌△CDF(AAS),∴BE=DF.

(2)四边形BEDF是平行四边形.

理由:∵BE⊥AC,DF⊥AC,

∴BE∥DF.

又∵BE=DF,

∴四边形BEDF是平行四边形.

[素养提升]

解:(1)证明:∵四边形ABCD为矩形,

∴∠B=∠C=90°,CD=AB,AD=BC,AD∥BC.

∵将△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处,∴△DEF≌△DEC,

∴DF=DC,∠DFE=∠C=90°,

∴DF=AB,∠AFD=90°,

∴∠AFD=∠B.

∵AD∥BC,∴∠DAF=∠AEB.

在△ABE和△DFA中,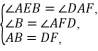

∴△ABE≌△DFA.

(2)∵EC∶BE=1∶4,

∴设EC=x,则BE=4x,∴AD=BC=5x.

由△ABE≌△DFA,得AF=BE=4x.

在Rt△ADF中,由勾股定理得DF==3x.

又∵DF=DC=AB=6,∴x=2,即EC=2.

在Rt△DCE中,DE===2.