湘教版数学八年级下册同步练习 2.3中心对称和中心对称图形

A[中心对称和中心对称图形]

一、选择题

1.下列图形是中心对称图形的是 (　　)

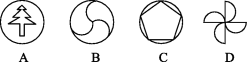
2.下列窗花图案中,是轴对称图形不是中心对称图形的是 (　　)

3.如图,△ABC与△A'B'C'关于点O成中心对称,则下列结论不成立的是 (　　)

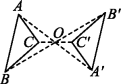
A.点A与点A'是对称点 B.BO=B'O

C.AB∥A'B'  D.∠ACB=∠C'A'B'

4.下列说法中,正确的有 (　　)

①线段两端点关于它的中点对称;

②平行四边形的一组对边关于对角线的交点对称;

③成中心对称的两个图形一定全等;

④如果两个图形全等,那么这两个图形一定关于某点成中心对称;

⑤如果两个三角形的对应点的连线都经过同一点,那么这两个三角形成中心对称.

A.2个 B.3个 C.4个 D.5个

二、填空题

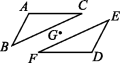
5.如图,如果△ABC和△DEF关于点G成中心对称,那么△ABC绕点G旋转　　　　°后能与△DEF重合. 

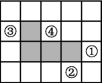
6.如图,在方格纸(每个小正方形的边长均相等)中,选择标有序号①②③④中的一个小正方形涂上阴影,与图中阴影部分构成中心对称图形,则该小正方形的序号是　　　　. 

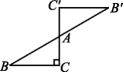
7.图是一个中心对称图形,点A为对称中心.若∠C=90°,∠B=30°,AC=1,则AB'的长是　　　　. 

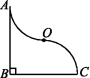
8.如图,AB⊥BC,AB=BC=2 cm,弧OA与弧OC关于点O成中心对称,则AB,BC,弧OC,弧OA所围成的图形的面积是　　　　cm2. 

三、解答题

9.如图分别是五角星、六角星、七角星、八角星的图形.

(1)其中的中心对称图形有哪些?

(2)依此类推,36角星是不是中心对称图形?

(3)怎样判断一个n(n是正整数)角星是不是中心对称图形?

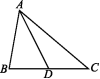
10.已知:如图,AD是△ABC的中线.

(1)画出与△ADC关于点D成中心对称的三角形;

(2)找出(1)中所画图形中与AC相等的线段;

(3)探索AB,AC的和与中线AD之间的关系,并说明理由;

(4)若AB=3,AC=5,直接写出线段AD的长的取值范围.

11.知识背景:过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.

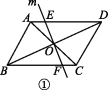
(1)如图①,直线m经过▱ABCD对角线的交点O,与AD边交于点E,与BC边交于点F,则S四边形AEFB　　　　S四边形DEFC(填“>”“<”或“=”); 

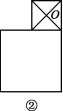
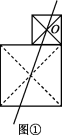
(2)两个正方形如图②所示摆放,O为小正方形对角线的交点,求作过点O的直线,使它将整个图形分成面积相等的两部分;

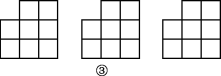
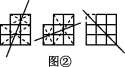
(3)八个大小相同的正方形如图③所示摆放,求作一条直线,使它将整个图形分成面积相等的两部分(用三种方法分割).

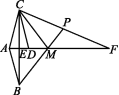
已知:如图,△ABM与△ACM关于直线AF成轴对称,△ABE与△DCE关于点E成中心对称,点E,D,M都在线段AF上,BM的延长线交CF于点P.

(1)求证:AC=DC;

(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.

图   

答案

1.D　2.B　3.D　4.B　

5.180　6.②

7. 2

 ∵此图形是中心对称图形,点A为对称中心,∴AB'=AB.∵∠C=90°,∠B=30°,AC=1,∴AB=2AC=2,∴AB'=AB=2.故答案为2.

8. 2

 由弧OA与弧OC关于点O成中心对称,根据中心对称的性质可知,若连接AC,则O为AC的中点,题中所求面积等于△BAC的面积.

[点评] 根据中心对称的性质,把所求的不规则图形的面积转化为规则图形的面积是解决本题的关键.

9.解:(1)中心对称图形有六角星,八角星.

(2)36角星是中心对称图形.

(3)当n是偶数时,n角星绕中心点旋转180°能与原来的图形完全重合,n角星是中心对称图形;

当n是奇数时,n角星绕中心点旋转180°不能与原来的图形完全重合,n角星不是中心对称图形.

10.解:(1)如图,△A'BD即为所求作的三角形.

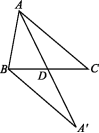
(2)根据中心对称的性质可得A'B=AC.

(3)AB+AC>2AD.理由如下:

由(2)知A'B=AC,

∴AB+AC=AB+A'B.

由中心对称的性质,知AD=A'D.

在△A'BA中,由三角形的两边之和大于第三边可知AB+A'B>AA',

即AB+AC>2AD.

(4)1<AD<4.

11.解:(1)=

(2)如图①所示.

(3)如图②所示.

[素养提升]

解:(1)证明:∵△ABM与△ACM关于直线AF成轴对称,

∴△ABM≌△ACM,

∴AB=AC.

∵△ABE与△DCE关于点E成中心对称,

∴△ABE≌△DCE,

∴AB=DC,

∴AC=DC.

(2)∠F=∠MCD.

理由:由(1)可得△ABM≌△ACM,AC=DC,

∴∠BAE=∠CAE=∠CDE,∠CMA=∠BMA.

∵∠BAC=2∠MPC,∠BMA=∠PMF,

∴∠MPC=∠BAE=∠CAE=∠CDE,∠PMF=∠CMA.

∵∠F=∠MPC-∠PMF,∠MCD=∠CDE-∠CMA,

∴∠F=∠MCD.