初中数学湘教版八年级下册2.1 多边形练习

[多边形的内角和]

一、选择题

1.如图所示的图形中,属于多边形的有 (　　)

A.3个 B.4个 C.5个 D.6个

2.图中的黑色正五边形的内角和是 (　　)

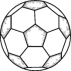
A.180° B.360° C.540° D.720°

3.正八边形的每一个内角的度数为 (　　)

A.120° B.135° C.140° D.144°

4.(2020济宁)一个多边形的内角和是1080°,则这个多边形的边数是 (　　)

A.9 B.8 C.7 D.6

5.从六边形的一个顶点出发,可以画出m条对角线,它们将六边形分成n个三角形,则m,n的值分别为              (　　)

A.4,3 B.3,3 C.3,4 D.4,4

二、填空题

6.(2020天门)已知正n边形的一个内角为135°,则n的值是　　　　.  

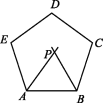
7.如图,过正五边形ABCDE的顶点B作一条射线与其内角∠EAB的平分线相交于点P,且∠ABP=60°,则∠APB=　　　　°. 

三、解答题

8.已知n边形的内角和p=(n-2)·180°.

(1)甲同学说:“p能取360°.”而乙同学说:“p也能取630°.”甲、乙两名同学的说法对吗?若对,求出边数n;若不对,请说明理由.

(2)若m边形变为(m+x)边形,发现内角和增加了360°,用列方程的方法确定x.

 [从特殊到一般的思想] 如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫作正多边形,如图是一组正多边形,观察每个正多边形中∠α的变化情况,解答下列问题.

　　(1)将下面的表格补充完整:

　　(2)是否存在一个正n边形,使∠α=20°?若存在,直接写出n的值;若不存在,请说明理由.

(3)是否存在一个正n边形,使∠α=21°?若存在,直接写出n的值;若不存在,请说明理由.

答案

1.A

2. C　黑色正五边形的内角和为(5-2)×180°=540°.

3.B

4. B　设这个多边形的边数为n,则有(n-2)·180°=1080°,解得n=8.

5.C

6. 8

 根据题意,得(n-2)·180°=n·135°,解之即得.

7. 66

 ∵五边形ABCDE为正五边形,

∴∠EAB=108°.

∵AP是∠EAB的平分线,∴∠PAB=54°.

又∵∠ABP=60°,

∴∠APB=180°-60°-54°=66°.

故答案为66.

8.解:(1)甲同学的说法对.∵p=360°,∴(n-2)·180°=360°,解得n=4.乙同学的说法不对.理由:∵p=630°,∴(n-2)·180°=630°,解得n=.∵n应为整数,∴p不能取630°.

(2)由题意,得(m+x-2)·180°-(m-2)·180°=360°,解得x=2,故x的值是2.

[素养提升]

解:(1)填表如下:

(2)存在一个正n边形,使∠α=20°,此时n=9.

(3)不存在.理由如下:假设存在一个正n边形,使∠α=21°,

根据题意,得=21°,

解得n=8.

因为n应是正整数,所以不存在一个正n边形,使∠α=21°.