以矩形为背景的折叠-中考数学复习课件PPT

这是一份以矩形为背景的折叠-中考数学复习课件PPT，共15页。PPT课件主要包含了背景分析，典例探究，方程思想，质疑合探，数学方法，数学思想，学习体验，收获满满，矩形的折叠，作业自助等内容，欢迎下载使用。
图形折叠问题是我们生活中常见的问题,也是中考的热点问题，2022年更是作为压轴题来考，它不仅是我们中考拿分的关键点，也是训练我们的动手操作能力、空间想象能力及灵活运用知识能力的有效途径。希望同学们加倍重视，把这部分知识学好、学透彻！
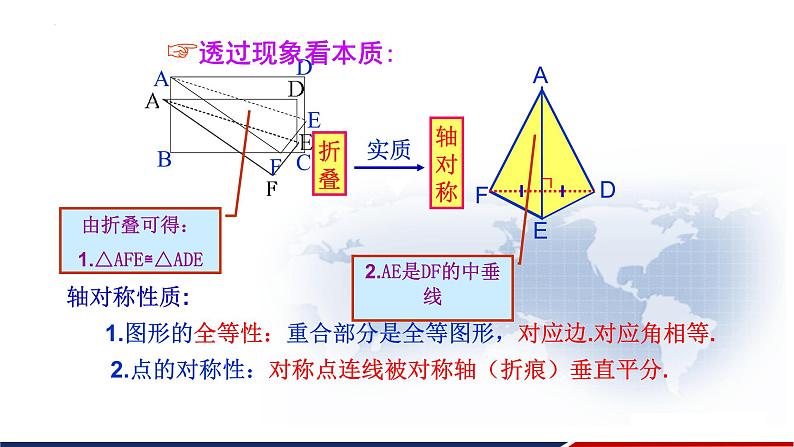
1.图形的全等性：重合部分是全等图形，对应边.对应角相等.
2.点的对称性：对称点连线被对称轴（折痕）垂直平分.
由折叠可得：1.△AFE≌△ADE
2.AE是DF的中垂线
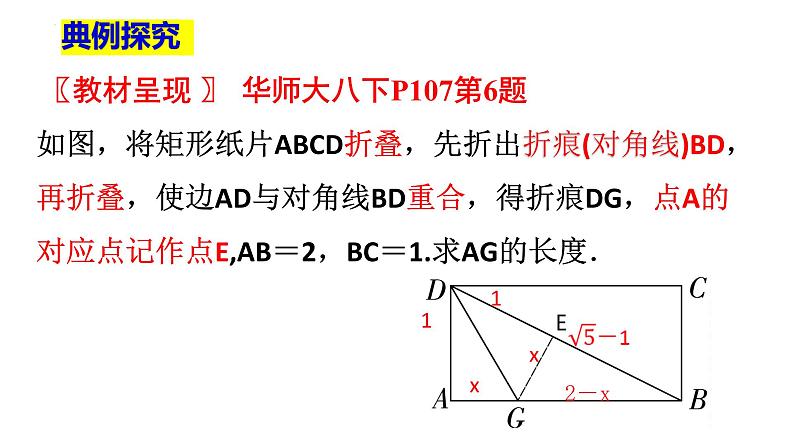
〖教材呈现 〗 华师大八下P107第6题如图，将矩形纸片ABCD折叠，先折出折痕(对角线)BD，再折叠，使边AD与对角线BD重合，得折痕DG，点A的对应点记作点E,AB＝2，BC＝1.求AG的长度．
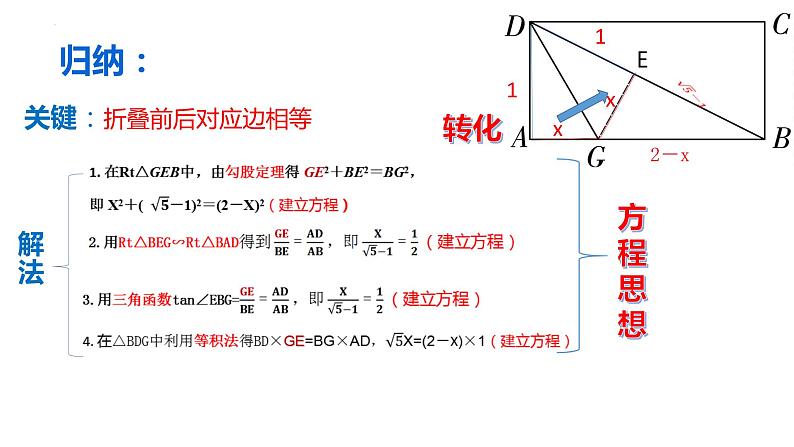
关键：折叠前后对应边相等
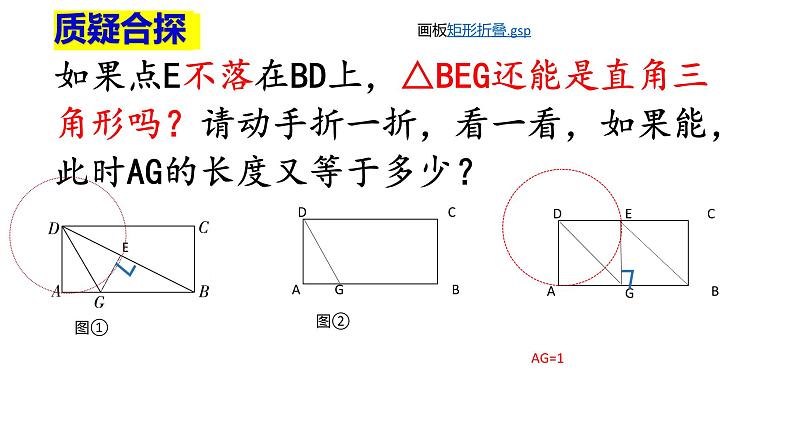
如果点E不落在BD上，△BEG还能是直角三角形吗？请动手折一折，看一看，如果能，此时AG的长度又等于多少？
(2022河南23题) 综合与实践综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动．(1)操作判断操作一：对折矩形纸片ABCD,使AD与BC重合,得到折痕EF，把纸片展平；
操作二：在AD上选一点P，沿BP折叠，使点A落在矩形内部点M处，把纸片展平，连PM、BM.根据以上操作，当点M在EF上时，写出图①中一个30°的角：_______
∠ABP（或∠EMB、∠MBC 、∠PBM)
解疑再探 （挑战中考）
(2)迁移探究 小华将矩形纸片换成正方形纸片，继续探究，过程如下：将正方形纸片ABCD按照(1)中的方式操作，并延长PM交CD于点Q，连接BQ.①如图②，当点M在EF上时，∠MBQ＝______°，∠CBQ＝______°；
Rt△MBQ≌Rt△CBQ（HL）.
②改变点P在AD上的位置(点P不与点A，D重合)，如图③，判断∠MBQ与∠CBQ的数量关系，并说明理由；
②∠MBQ＝∠CBQ；∵四边形ABCD是正方形，∴AB＝BC，∠A＝∠C＝90°.由折叠的性质得，BM＝AB，∠BMP＝∠A＝90°.∴∠BMQ＝∠C＝90°，BM＝BC.∵BQ是公共边，∴Rt△MBQ≌Rt△CBQ(HL).∴∠MBQ＝∠CBQ；
(3)拓展应用 在(2)的探究中，已知正方形纸片ABCD的边长为8 cm，当FQ＝1 cm时，直接写出AP的长．
数学思想：分类讨论，从特殊到一般，类比、转化
在Rt△PDQ中，由勾股定理得(8－x)2＋52＝(3＋x)2
这节课，我的收获是——
必做：1.长方形ABCD如图折叠，使点D落在 BC边上的点F处，已知AB=8，BC=10，求 CE的长。选做：2.如图，在矩形ABCD 中，AD=2，AB=3， 点E是AD 边的中点，点F是射线AB上的一动点， 将ΔAEF沿EF所在的直线翻折得到△A'EF，连接A'C， 则A'C的最小值为_ 。