2022-2023学年河北省廊坊市广阳区八年级（下）期末数学试卷（含解析）

这是一份2022-2023学年河北省廊坊市广阳区八年级（下）期末数学试卷（含解析），共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年河北省廊坊市广阳区八年级（下）期末数学试卷
一、选择题（本大题共16小题，共42.0分。在每小题列出的选项中，选出符合题目的一项）
1. 若 x在实数范围内有意义，则x的取值范围为(    )
A. x≥0 B. x≤0 C. x=0 D. x为任意实数
2. 下列二次根式是最简二次根式的是(    )
A. 12 B. 7 C. 8 D. 0.3
3. 下列各式能够与 3进行合并的是(    )
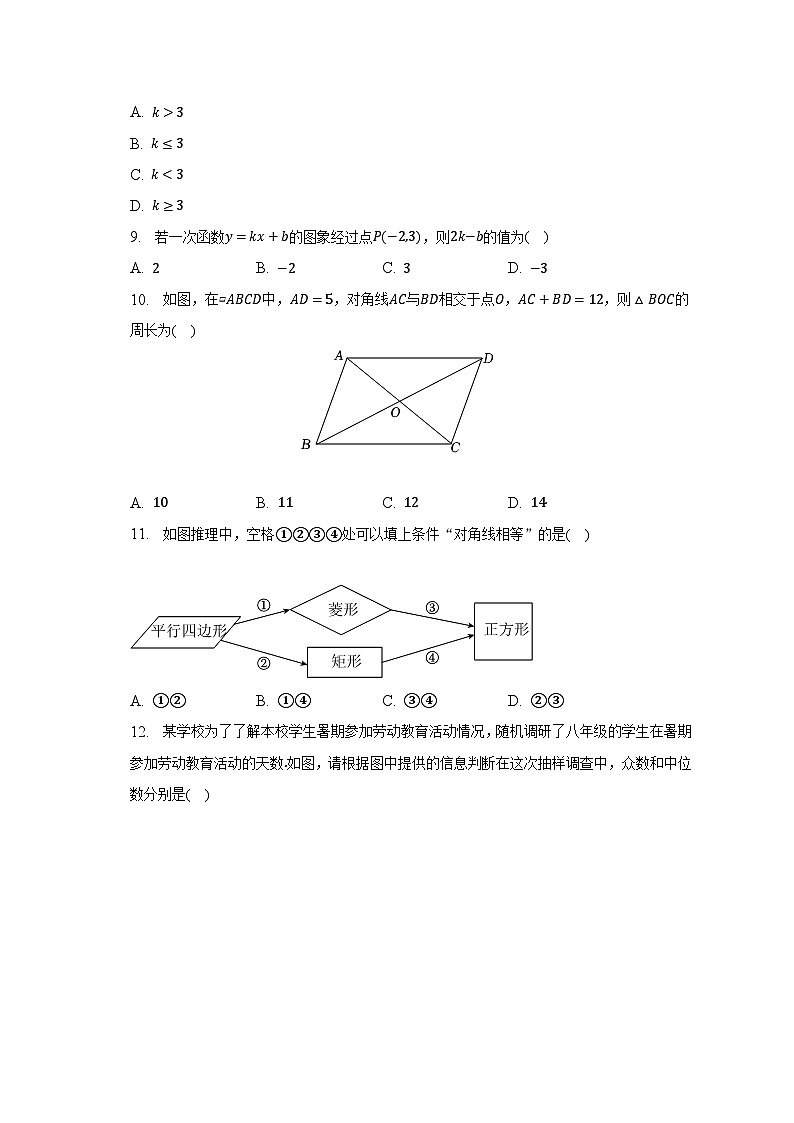
A. 8 B. 24 C. 125 D. 12
4. 第27届LG杯世界棋王赛决赛将于2023年2月举行，这也是2023年第一个世界围棋大赛决赛.如图是一个围棋棋盘的局部，若棋盘是由边长均为1的小正方形组成的，则黑、白两棋子的距离为(    )
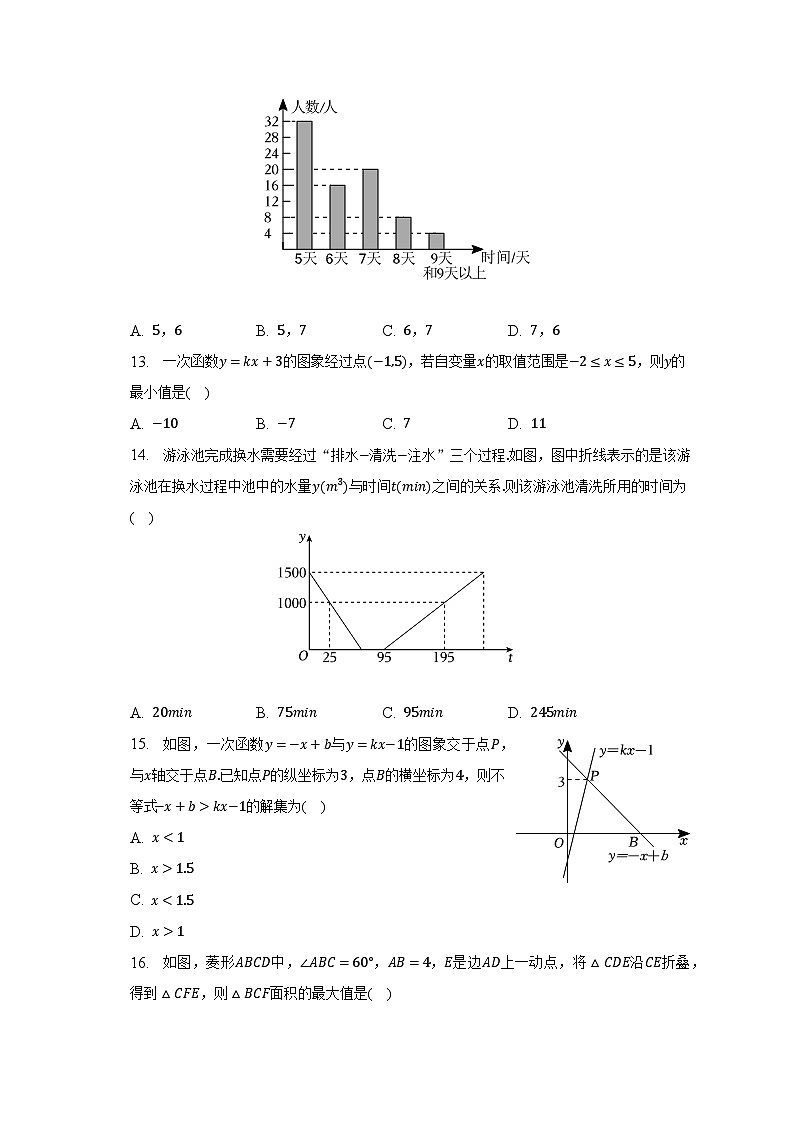
A. 2
B. 3
C. 2 3
D. 2 5
5. 如图，以直角三角形的三边为边向外作正方形，根据图中数据，可得出正方形A的面积是(    )
A. 12
B. 24
C. 30
D. 10
6. 下列各组数能作为直角三角形的三边长的是(    )
A. 1，3， 10 B. 9，16，25 C. 2，2，4 D. 10，24，28
7. 下列函数中，是一次函数的是(    )
A. y=12x+1 B. y=2x+1
C. y=x2+1 D. y=kx+b(k、b是常数)
8. 正比例函数y=(k−3)x的图象如图，则k的取值范围为(    )
A. k>3
B. k≤3
C. kkx−1的解集为(    )
A. x1.5
C. x1
16. 如图，菱形ABCD中，∠ABC=60°，AB=4，E是边AD上一动点，将△CDE沿CE折叠，得到△CFE，则△BCF面积的最大值是(    )

A. 8 B. 8 3 C. 16 D. 16 3
二、填空题（本大题共3小题，共9.0分）
17. 若代数式 x+3x−1有意义，则字母x的取值范围是______．
18. 如图，在平行四边形ABCD中，AD=5，AB=3，∠BAD的平分线AE交BC于E点，则EC的长为______．


19. 小强家因装修准备用电梯搬运一些木条上楼，如图，已知电梯的长、宽、高分别是1.2m，0.9m，2m，那么电梯内能放入这些木条的最大长度是        m.


三、解答题（本大题共7小题，共69.0分。解答应写出文字说明，证明过程或演算步骤）
20. (本小题8.0分)
计算：
(1) 18− 8+ 4；
(2)(2 48−3 27)÷ 6．
21. (本小题8.0分)
已知一次函数y=2x+4．
(1)求图象与x轴的交点A的坐标，与y轴交点B的坐标；
(2)在(1)的条件下，求出△AOB的面积．

22. (本小题8.0分)
《九章算术》中的“折竹抵地”问题：今有竹高一丈，末折抵地，去根三尺，问折高者几何？意思是：一根竹子，原高一丈(一丈=10尺)，一阵风将竹子折断，其竹稍恰好抵地，抵地处离竹子底部3尺远，问折断处离地面的高度是多少？

23. (本小题10.0分)
如图，在平行四边形ABCD中，E，F分别是边AD，BC上的点，且AE=CF．
(1)求证：BE=DF；
(2)连接AF，若BC=DF，∠DFC=36°，求∠AFB的度数．

24. (本小题12.0分)
甲、乙两名同学本学期五次某项测试的成绩(单位：分)如图所示．

(1)甲、乙两名同学五次测试成绩的平均数分别是______ 分、______ 分；
(2)利用方差判断这两名同学该项测试成绩的稳定性；
(3)结合数据，请再写出一条与(1)(2)不同角度的结论．
25. (本小题10.0分)
金百超市经销某品牌童装，单价为每件50元时，每天销量为60件，当单价每件从50元降了20元时，一天销量为100件．设降x元时，一天的销量为y件．已知y是x的一次函数．
(1)求y与x之间的关系式；
(2)若某天销售童装80件，则该天童装的单价是多少？
26. (本小题13.0分)
如图，在▱ABCD中，∠ABC为锐角，AB=5，BC=9，S▱ABCD=36.动点P从点A出发，以每秒2个单位的速度沿A→B→C→D→A运动.同时，动点Q从点A出发，以每秒3个单位的速度沿A→D→C→B→A运动.当其中一个点到达终点时，另一个点也随之停止运动.设点P的运动时间为t秒．
(1)点P在BC上运动时，CP= ______ ；点P在CD上运动时，CP= ______ .(用含t的代数式表示)
(2)点P在CD上，PQ//BC时，求t的值．
(3)当直线PQ平分▱ABCD的面积时，求t的值．
(4)若点Q的运动速度改变为每秒a个单位.当923．
故选：A．
由正比例函数的图象过第一和第三象限，即可求出k的取值范围．
本题考查正比例函数的图象和系数的关系，关键是掌握正比例函数的图象和性质．

9.【答案】D 
【解析】解：把点(−2,3)代入一次函数y=kx+b，可得：3=−2k+b，
所以2k−b=−3，
故选：D．
直接把点(−2,3)代入一次函数y=kx+b，求出k，b的关系即可．
本题考查的是一次函数图象上点的坐标特点，熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．

10.【答案】B 
【解析】解：∵四边形ABCD是平行四边形，
∴AO=OC=12AC，BO=OD=12BD，AD=BC=5，
∵AC+BD=12，
∴OC+BO=6，
∴C△BOC=OC+OB+BC=6+5=11，
故选：B．
根据平行四边形对角线平分可得OC+BO=6，即可求出结果．
本题考查平行四边形的性质及三角形周长，熟练掌握平行四边形的对角线互相平分是解题的关键．

11.【答案】D 
【解析】解：∵对角线相等的平行四边形是矩形，
∴②处应该填上条件“对角线相等”；
∵对角线相等的菱形是正方形，
∴③处应该填上条件“对角线相等”．
故选：D．
由菱形，矩形，正方形的判定，即可解决问题．
本题考查菱形，矩形，正方形的判定，关键是掌握菱形，矩形，正方形的判定方法．

12.【答案】A 
【解析】解：观察数据可知，5出现的次数最多，故众数为5；
把这次抽样的80个数据从小到大排列，排在中间的两个数都是6，则中位数为6．
故选：A．
根据中位数、众数的定义即可求得．
本题考查中位数、众数，理解中位数、众数的定义，掌握中位数、众数的计算方法是正确解答的前提．

13.【答案】B 
【解析】解：一次函数y=kx+3的图象经过点(−1,5)，
∴5=−k+3，
解得：k=−2，
∴y=−2x+3，
∵k=−2，
∴y随x的增大而减小，
∵−2≤x≤5，
∴当x=5时，y的最小值为−2×5+3=−7．
故选：B．
根据待定系数法确定一次函数的解析式，再由一次函数的性质求出y的最小值即可．
本题主要考查一次函数解析式，一次函数的性质等，熟练掌握一次函数的性质是解题的关键．

14.【答案】A 
【解析】解：由图象可得，
排水的速度为：(1500−1000)÷25
=500÷25
=20(m3/min)，
∴排水用的时间为：1500÷20=75(min)，
清洗用的时间为：95−75=20(min)，
故选：A．
根据函数图象中的数据，可以计算出排水的速度，从而可以求得排水用的时间，然后再根据函数图象中的数据，即可计算出该游泳池清洗所用的时间．
本题考查一次函数的应用，解答本题的关键是明确题意，利用数形结合的思想解答．

15.【答案】A 
【解析】解：把B(4,0)代入y=−x+b得−4+b=0，
解得b=4，
∴一次函数y=−x+b的解析式为y=−x+4，
当y=3时，−x+4=3，
解得x=1，
∴P点坐标为(1,3)，
∴不等式−x+b>kx−1的解集为x