


天津市2021届高三上学期10月联考数学试卷 Word版含答案
展开
这是一份天津市2021届高三上学期10月联考数学试卷 Word版含答案,共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
天津市2020-2021学年度第一学期高三联考数学试卷一、选择题(每题5分,共45分)1.命题![]() :“
:“![]() ,都有
,都有![]() ”,则命题
”,则命题![]() 的否定为( )A.
的否定为( )A.![]() ,都有
,都有![]() B.
B.![]() ,使
,使![]() C.
C.![]() ,都有
,都有![]() D.
D.![]() ,使
,使![]() 2.已知集合
2.已知集合![]() ,
,![]() ,则
,则![]() ( )A.
( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.已知复数
3.已知复数![]() 满足
满足![]() ,则
,则![]() 的共轭复数在复平面内对应的点位于( )A.第一象限 B.第二象限 C.第三象限 D.第四象限4.设
的共轭复数在复平面内对应的点位于( )A.第一象限 B.第二象限 C.第三象限 D.第四象限4.设![]() ,
,![]() ,
,![]() ,则( )A.
,则( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.已知
5.已知![]() 的最大值为
的最大值为![]() ,其图像相邻两条对称轴之间的距离为
,其图像相邻两条对称轴之间的距离为![]() ,且
,且![]() 的图像关于点
的图像关于点![]() 对称,则下列判断错误的是( )A.要得到函数
对称,则下列判断错误的是( )A.要得到函数![]() 的图像,只需要现将
的图像,只需要现将![]() 的图像保持纵坐标不变,横坐标变为原来的一半,再向右平移
的图像保持纵坐标不变,横坐标变为原来的一半,再向右平移![]() 个单位B.函数
个单位B.函数![]() 的图像关于直线
的图像关于直线![]() 对称C.函数
对称C.函数![]() 在
在![]() 上单调递减D.当
上单调递减D.当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() 6.函数
6.函数![]() 的图象大致为( )A.
的图象大致为( )A.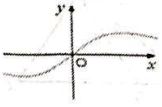 B.
B. C.
C. D.
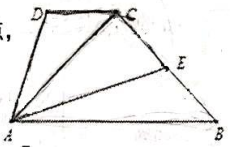
D.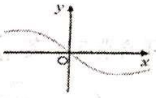 7.如图,在四边形
7.如图,在四边形![]() 中,
中,![]() ,
,![]() 为边
为边![]() 的中点,若
的中点,若![]() ,则
,则![]() ( )
( ) A.
A.![]() B.
B.![]() C.1 D.
C.1 D.![]() 8.在
8.在![]() 中,角
中,角![]() ,
,![]() ,
,![]() 所对的边分别为
所对的边分别为![]() ,
,![]() ,
,![]() ,则“
,则“![]() ”,是“
”,是“![]() 为锐角三角形”的( )条件A.充分必要 B.充分不必要 C.必要不充分 D.既不充分也不必要9.设函数
为锐角三角形”的( )条件A.充分必要 B.充分不必要 C.必要不充分 D.既不充分也不必要9.设函数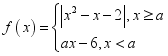 ,满足对任意的实数
,满足对任意的实数![]() 都有
都有![]() 成立,则实数
成立,则实数![]() 取值范围( )A.
取值范围( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(每题5分,共30分)10.已知
二、填空题(每题5分,共30分)10.已知![]() 为虚数单位,则
为虚数单位,则![]() ______.11.已知
______.11.已知![]() ,则
,则![]() 的值为______.12.已知函数
的值为______.12.已知函数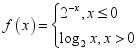 ,则
,则![]() 的取值范围是______.13.设
的取值范围是______.13.设![]() 为定义在
为定义在![]() 上的奇函数,
上的奇函数,![]() 与
与![]() 关于直线
关于直线![]() 对称,若当
对称,若当![]() 时,
时,![]() ,则
,则![]() ______.14.如图,在
______.14.如图,在![]() 中,
中,![]() ,点
,点![]() 在线段
在线段![]() 上移动(不含端点),若
上移动(不含端点),若![]() ,则
,则![]() ______,
______,![]() 的最小值是______.
的最小值是______.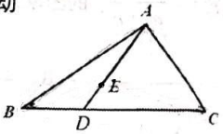 15.已知函数
15.已知函数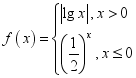 .若函数
.若函数![]() 存在5个零点,则实数
存在5个零点,则实数![]() 的取值范围为______.三、解答题(共75分)16.已知集合
的取值范围为______.三、解答题(共75分)16.已知集合![]() ,
,![]() .(1)若
.(1)若![]() ,求集合
,求集合![]() ,集合
,集合![]() ;(2)若
;(2)若![]() ,求实数
,求实数![]() 的取值范围.17.在
的取值范围.17.在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为三个内角
分别为三个内角![]() ,
,![]() ,
,![]() 的对边,
的对边,![]() .(1)求角
.(1)求角![]() 的大小;(2)若
的大小;(2)若![]() ,
,![]() ,求
,求![]() 和
和![]() 的值.18.已知函数
的值.18.已知函数![]() 的周期为
的周期为![]() .(1)求
.(1)求![]() ;(2)求函数
;(2)求函数![]() 的对称中心;(3)已知
的对称中心;(3)已知![]() ,
,![]() ,求
,求![]() 的值.19.已知
的值.19.已知![]() ,函数
,函数![]() .(1)若
.(1)若![]() ,求
,求![]() 在
在![]() 处的切线方程;(2)若函数
处的切线方程;(2)若函数![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的取值范围;(3)讨论函数
的取值范围;(3)讨论函数![]() 的单调区间.20.已知函数
的单调区间.20.已知函数![]() .(1)若
.(1)若![]() ,求
,求![]() 的最小值;(2)当
的最小值;(2)当![]() 时,若不等式
时,若不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;(3)当
的取值范围;(3)当![]() 时,证明
时,证明![]() .参考答案一、选择题1.B 2.B 3.C 4.A 5.D 6.A 7.D 8.C 9.D二、填空题10.
.参考答案一、选择题1.B 2.B 3.C 4.A 5.D 6.A 7.D 8.C 9.D二、填空题10.![]() 11.
11.![]() 12.
12.![]() 13.
13.![]() 14.(1)2 (2)
14.(1)2 (2)![]() 15.
15.![]() 三、解答题16.(1)
三、解答题16.(1)![]() ,
,![]() .
.![]() .
.![]() .(2)因为
.(2)因为![]() ,所以
,所以![]() .当
.当![]() 时,
时,![]() ,则
,则![]()
![]() ;当
;当![]() 时,由题意得
时,由题意得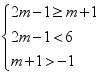 ,解得
,解得![]() .综上,实数
.综上,实数![]() 的取值范围是
的取值范围是![]() .17.(1)由已知,得:
.17.(1)由已知,得:![]() ,由余弦定理,即
,由余弦定理,即![]() ,所以
,所以![]() .(2)
.(2)![]() ,∴
,∴![]()
![]() ∴
∴![]() ,∴
,∴![]() ,又
,又![]() ,∴
,∴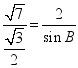 ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() .18.(1)∵
.18.(1)∵![]() ,
,![]() (2)
(2)![]()
![]() 因此,函数
因此,函数![]() 的对称中心为
的对称中心为![]() (2)由题意可得∵
(2)由题意可得∵![]() ,∴
,∴![]() ,∵
,∵![]() ,
,![]() ,则
,则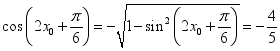 ,因此,
,因此,![]()
![]()
![]() .19.(1)
.19.(1)![]() 时,
时,![]() 的导数为
的导数为![]() ,
,![]()
![]() 切线
切线![]() (2)函数
(2)函数![]() 的导数为
的导数为![]()
![]() 在
在![]() 上恒成立
上恒成立![]()
![]() ∵
∵![]() ,∴
,∴![]() (3)
(3)![]()
![]() ①
①![]() 时
时![]() ②
②![]() 时
时![]() ③
③![]() 时
时![]() 20.(1)
20.(1)![]() ,
,![]() 令
令![]() ,解得
,解得![]()
![]() 在
在![]()
![]() (2)由条件得
(2)由条件得![]() ,令
,令![]() ,则
,则![]() .①当
.①当![]() 时,在
时,在![]() 上,
上,![]() ,
,![]() 单调递增∴
单调递增∴![]() ,即
,即![]() ,∴
,∴![]() 在
在![]() 上为增函数,∴
上为增函数,∴![]() ,∴
,∴![]() 时满足条件.②当
时满足条件.②当![]() 时,令
时,令![]() 解得
解得![]() ,在
,在![]() 上,
上,![]() ,
,![]() 单调递减,∴当
单调递减,∴当![]() 时,有
时,有![]() ,即
,即![]() ,
,![]() 在
在![]() 上为减函数,∴
上为减函数,∴![]() ,不合题意.综上实数
,不合题意.综上实数![]() 的取值范围为
的取值范围为![]() .(3)由(1)得,当
.(3)由(1)得,当![]() ,
,![]() 时,
时,![]() ,即
,即![]() ,要证不等式
,要证不等式![]() ,只需证明
,只需证明![]() ,只需证明
,只需证明![]() ,只需证
,只需证![]() ,设
,设![]() ,则
,则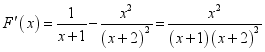 ,∴当
,∴当![]() 时,
时,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,∴
,∴![]() 恒成立.∴原不等式成立.
恒成立.∴原不等式成立.
相关试卷
这是一份天津市八所重点学校2023-2024学年高三上学期期末联考试题 数学 Word版含答案,文件包含天津市八校联考2023-2024学年高三上学期期末质量调查数学试卷docx、天津市八校联考2023-2024学年高三上学期期末质量调查数学答案pdf等2份试卷配套教学资源,其中试卷共15页, 欢迎下载使用。
这是一份天津市和平区2021届高三上学期期中质量调查数学试卷 Word版含答案,共5页。
这是一份天津市八校2021届高三上学期期中联考数学试题 Word版含答案,文件包含高三数学答案doc、2020-2021学年第一学期期中联考高三数学试卷docx、高三数学答题卡doc等3份试卷配套教学资源,其中试卷共15页, 欢迎下载使用。








