


天津市红桥区2021届高三上学期期中质量检测数学试题 Word版含答案
展开
这是一份天津市红桥区2021届高三上学期期中质量检测数学试题 Word版含答案,共12页。试卷主要包含了每小题给出答案后,75,连续两天为优良的概率是0等内容,欢迎下载使用。
红桥区2021届高三上学期期中质量检测数学 本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共150分,考试时间120分钟。 答卷前,考生务必将自己自己的姓名、考生号、考场号和座位号填写在答题卡上,并在规定位置粘贴考试用条形码。答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。考试结束后,将本试卷和答题卡一并交回。 祝各位考生考试顺利!第I卷注意事项: 1.每小题给出答案后。用铅笔把答题卡上对用题目的答案标号涂黑。如需改动,用相扑擦干净后,再选涂其它答案标号。2.本卷共10题,每小题5分,共50分。 参考公式: 如果事件A与事件B互斥,那么. 如果事件A与事件B相互独立,那么. 柱体体积公式:,其中表示柱体底面积,表示柱体的高. 锥体体积公式:,其中表示锥体底面积,表示锥体的高. 球体表面积公式:,其中表示球体的半径. 球体体积公式:,其中表示球体的半径.一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.(1)若全集,集合,集合,则( ) (A) (B) (C) (D)(2)命题“”的否定为( ) (A) (B) (C) (D)(3)已知A是三角形ABC的内角,则“”是“”的 ( ) (A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既不充分也不必要条件(4)已知, 则等于 ( ) (A) (B) (C) (D)(5)为了得到函数的图像,可以将函数的图像( ) (A)向右平移个单位长度 (B)向右平移个单位长度 (C)向右平移个单位长度 (D)向左平移个单位长度(6)设,向量,若∥,则 ( ) (A)1 (B) (C)2 (D)(7)某地区空气质量检测资料表明,一天的空气质量为优良的概率是0.75,连续两天为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是( ) (A)0.75 (B)0.80 (C)0.60 (D)0.45(8)设随机变量,则( ) (A)0 (B)1 (C) (D)(9)已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是( ) (A)10 (B)20 (C)24 (D)32(10)已知是不重合的直线,,是不重合的平面,有下列命题: ①若∥,,则∥; ②若∥,∥,则∥; ③若,,则∥; ④若,,则∥; ⑤若,,则; ⑥若∥,,则;⑦若,∥,则∥. 其中真命题的个数是( ) (A)2 (B)3 (C)4 (D)5二、填空题:本大题共6小题,每小题5分,共30分.(11)设为虚数单位,则复数的共轭复数 .(12)的二项展开式中,的系数是 .(用数字作答)(13)平面向量,中,已知,,且,则向量 .(14)某一天上午的课程表要排入语文、数学、物理、体育共4节课,如果第一节不排体育,最后一节不排数学,那么共有排法 种. (用数字作答)(15)某射手每次射击击中目标的概率是0.8,则这名射手在3次射击恰好有1次击中目标的概率是 .(16)已知是边长为1的等边三角形,点分别是边的中点,连接并延长到点,使得,则的值为 .三、解答题:本大题共5个题,共70分.解答题应写出文字说明、证明过程或演算步骤.17.(本小题满分10分)某商场拟通过摸球兑奖的方式对1000位顾客进行奖励,袋中所装的4个球中有1个所标的面值为50元,其余3个均为10元. 规定:每位顾客从袋中一次性随机摸出2个球,球上所标的面值之和为该顾客所获的奖励额.(I)求顾客所获的奖励额为60元的概率;(II)求顾客所获的奖励额的分布列及数学期望. (18)(本小题满分15分)在中,分别为内角的对边,已知,,.(I)求的值(II)求的值
19.(本小题满分15分)已知函数.(I)求函数的最小正周期;(II)求函数在上的单调递增区间和最小值. (20)(本小题满分15分) 如图,在四棱锥O﹣ABCD中,底面ABCD是边长为1的菱形,∠ABC=
如图,在四棱锥O﹣ABCD中,底面ABCD是边长为1的菱形,∠ABC=![]() ,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.(I)证明:直线MN∥平面OCD;(II)求异面直线AB与MD所成角的余弦值.
,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.(I)证明:直线MN∥平面OCD;(II)求异面直线AB与MD所成角的余弦值.
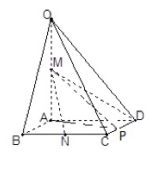
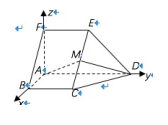
(21)(本小题满分15分)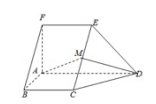 如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=
如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=![]() AD.(I)证明:平面AMD⊥平面CDE;(II)求二面角A﹣CD﹣E的余弦值.
AD.(I)证明:平面AMD⊥平面CDE;(II)求二面角A﹣CD﹣E的余弦值. ![]()
参考答案一、选择题(每小题5分,共50分)题号(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)答案DCAABDBCCA二、填空题(每小题5分,共30分)(11); (12); (13); (14)14; (15)0.096; (16);三、解答题(本大题共5小题,共70分)17.(本小题满分10分)解:(I)设顾客所获取的奖励额为X,依题意,得P(X=60)=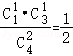 ,即顾客所获得奖励额为60元的概率为
,即顾客所获得奖励额为60元的概率为![]() ,(II)依题意得X得所有可能取值为20,60,P(X=60)=
,(II)依题意得X得所有可能取值为20,60,P(X=60)=![]() ,P(X=20)=
,P(X=20)=![]() ,即X的分布列为 X2060P
,即X的分布列为 X2060P ![]()
![]() 所以这位顾客所获的奖励额的数学期望为E(X)=20×
所以这位顾客所获的奖励额的数学期望为E(X)=20×![]() +60×
+60×![]() =40(18)(本小题满分15分)解:(Ⅰ)由余弦定理
=40(18)(本小题满分15分)解:(Ⅰ)由余弦定理![]() ………………………3
………………………3![]() 所以
所以![]() ………………………………………….7(Ⅱ)由正弦定理
………………………………………….7(Ⅱ)由正弦定理![]() 所以
所以![]() ……………11所以
……………11所以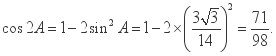 ……………… 1519.(本小题满分15分)解:(Ⅰ)
……………… 1519.(本小题满分15分)解:(Ⅰ)![]() ……………………….6
……………………….6 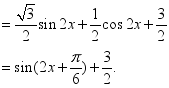 …………………………………8
…………………………………8 ![]() 的最小正周期
的最小正周期![]() ……………………………………….10 (Ⅱ)
……………………………………….10 (Ⅱ)![]() 的单调增区间为:
的单调增区间为:![]() 即
即 ![]() f(x)在
f(x)在![]() 上的单调增区间为, 在
上的单调增区间为, 在![]() 上, f(0)=2,f()= ,
上, f(0)=2,f()= ,![]() min= …………………………….15(20)(本小题满分15分)方法一:(Ⅰ)证明:取OD的中点E……………………………..1
min= …………………………….15(20)(本小题满分15分)方法一:(Ⅰ)证明:取OD的中点E……………………………..1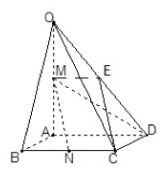 ∵M为OA的中点
∵M为OA的中点 ![]() ∵N为BC的中点∴
∵N为BC的中点∴![]()
![]() ∴四边形MNCE是平行四边形…………………………………3∴MN∥EC∵MN平面OCD,EC平面OCD,∴MN∥平面OCD.………………………………………………7(Ⅱ)解:
∴四边形MNCE是平行四边形…………………………………3∴MN∥EC∵MN平面OCD,EC平面OCD,∴MN∥平面OCD.………………………………………………7(Ⅱ)解:![]()
![]() 为异面直线
为异面直线![]() 与
与![]() 所成的角(或其补角)………10作
所成的角(或其补角)………10作![]() 连接
连接![]() ,
,
![]() ∴OA
∴OA![]() CD∴CD
CD∴CD![]() 平面OAP∵MP平面OAP∴CD
平面OAP∵MP平面OAP∴CD![]() MP
MP![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() 所以
所以 ![]() 与
与![]() 所成角的大小为
所成角的大小为![]() ………………………………………15方法二:(Ⅰ)证明:作
………………………………………15方法二:(Ⅰ)证明:作![]() 于点P,如图,分别以AB,AP,AO所在直线为
于点P,如图,分别以AB,AP,AO所在直线为![]() 轴建立坐标系..............................2
轴建立坐标系..............................2![]() ,
,![]() ,
, ![]() …………..4设平面
…………..4设平面![]() 的法向量为
的法向量为![]() ,则 =0,=0
,则 =0,=0 即
即 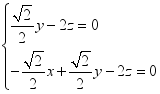 取
取![]() ,解得
,解得![]() ...............7 ∵=0
...............7 ∵=0![]() .............................................9(Ⅱ)解:设
.............................................9(Ⅱ)解:设![]() 与
与![]() 所成的角为
所成的角为![]() ,
,![]() ......11
......11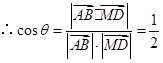 …………………………………………….13
…………………………………………….13![]() ,
,![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .......................................15(21)(本小题满分15分)方法一:(Ⅰ)证明:取
.......................................15(21)(本小题满分15分)方法一:(Ⅰ)证明:取![]() 的中点
的中点![]() ,连结
,连结![]()
 ∵
∵![]() ,∴四边形FAPE是平行四边形∴
,∴四边形FAPE是平行四边形∴![]() .同理,
.同理,![]() .又∵
.又∵![]() ,∴
,∴![]() 而
而![]() 都在平面
都在平面![]() 内,∴
内,∴![]() 由
由![]() 设
设![]() ,则
,则![]() 所以△ECD为正三角形.∵
所以△ECD为正三角形.∵![]() 且
且![]() 为
为![]() 的中点,∴
的中点,∴![]() .连结
.连结![]() ,则
,则![]() PM∩MD=M, 而PM,MD在平面AMD内 ∴
PM∩MD=M, 而PM,MD在平面AMD内 ∴![]() ……………………….…………...5而
……………………….…………...5而![]() 平面
平面![]() .…………………7(Ⅱ)解:取
.…………………7(Ⅱ)解:取![]() 的中点,连结
的中点,连结![]() …………………………8∵
…………………………8∵![]() ,∴
,∴![]() ∵
∵![]() ,∴
,∴![]() ∴
∴![]() 为二面角
为二面角![]() 的平面角.……………………………12由(Ⅰ)可得,
的平面角.……………………………12由(Ⅰ)可得,![]() 于是在
于是在![]()
 ∴二面角
∴二面角![]() 的余弦值为
的余弦值为![]() .……………………………15方法二:如图所示,建立空间直角坐标系,点
.……………………………15方法二:如图所示,建立空间直角坐标系,点![]() 为坐标原点.设
为坐标原点.设![]() ,依题意得
,依题意得![]() .(Ⅰ)证明:由 又AM∩AD=A故
.(Ⅰ)证明:由 又AM∩AD=A故![]() ……………………………………………………5而
……………………………………………………5而![]() ,所以平面
,所以平面![]() .……………………7(Ⅱ)解:设平面
.……………………7(Ⅱ)解:设平面![]() 的法向量为) 则,于是
的法向量为) 则,于是![]() 令
令![]() ,可得).……………………………………………10又由题设,平面
,可得).……………………………………………10又由题设,平面![]() 的一个法向量为).所以,
的一个法向量为).所以,![]() .因为二面角
.因为二面角![]() 为锐角,所以其余弦值为
为锐角,所以其余弦值为![]() .…………………15
.…………………15
相关试卷
这是一份2023届天津市红桥区高三上学期期末数学试题含答案,共12页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份2022-2023学年天津市红桥区高三上学期期末数学试题含答案,文件包含天津市红桥区2022-2023学年高三上学期期末数学试题Word版含解析docx、天津市红桥区2022-2023学年高三上学期期末数学试题Word版无答案docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
这是一份天津市和平区2021届高三上学期期中质量调查数学试卷 Word版含答案,共5页。









