初中数学1.1 直角三角形的性质与判定（Ⅰ）课堂检测

[含30 °角的直角三角形的性质及应用]

一、选择题

1.(2020常德五中月考)如图,在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=12 cm,则AB的长度为(　　)

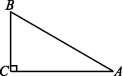
A.6 cm B.7 cm C.8 cm D.9 cm

2.如图,已知在△ABC中,∠ACB=90°,∠B=30°,D为斜边AB的中点,则图中与线段AC的长度相等的线段有(　　)

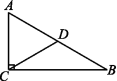
A.0条 B.1条 C.2条 D.3条

3.如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠A=30°,AB=4,则BD的长为(　　)

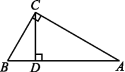
A.3 B.2 C.1 D.

4.已知三角形的三个内角度数之比为1∶2∶3,若这个三角形的最短边长为,则它的最长边长为              (　　)

A.2 B.2 C.3 D.3

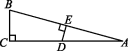
5.(2020怀化六中期中)如图,∠ACB=90°,AC=AB,CD⊥AB于点D,AD=ED,则图中30°角的个数是              (　　)

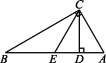
A.2 B.3 C.4 D.5

6.如图,在△ABC中,AB=BC,∠ABC=120°,过点B作BD⊥BC,交AC于点D,若AD=1,则CD的长度为              (　　)

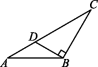
A.1 B.2 C.3 D.4

7.如图,已知∠1=∠2,AD=BD=4,CE⊥AD于点E,2CE=AC,那么CD的长是 (　　)

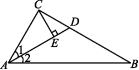
A.2 B.3 C.1 D.1.5

二、填空题

8.在△ABC中,∠C=90°,∠B=30°,AB=10,则AC=　　　　. 

9.在直角三角形中,最长边长为10 cm,最短边长为5 cm,则这个直角三角形中最小的内角为　　　　度. 

10.如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D.若CD=1,则BD=　　　　. 

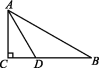
11.如图,在△ABC中,∠C=90°,DE垂直平分AB于点E,交AC于点D,AD=2BC,则∠A=　　　　°.               

12.等腰三角形一腰上的高与腰之比为1∶2,则等腰三角形顶角的度数为　　　　　　. 

三、解答题

13.如图所示,在四边形ACBD中,AD∥BC,AB⊥AC,且AC=BC,求∠DAC的度数.

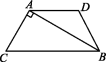
图   

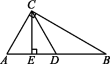
14.如图,在△ABC中,∠ACB=90°,∠B=30°,CE⊥AB于点E,D是AB的中点.

(1)求证:AE=DE;

(2)若AC=2,求DE的长.

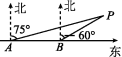
15.如图,某轮船由西向东航行,在A处测得小岛P在北偏东75°方向,又继续航行7海里后到达B处,在B处测得小岛P在北偏东60°方向.

(1)求此时轮船与小岛P的距离BP;

(2)小岛P 3海里内有暗礁,如果轮船继续向东行驶,请问轮船有没有触礁的危险,请说明理由.

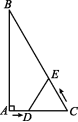
16.如图,在△ABC中,∠A=90°,∠B=30°,AC=6 cm,点D从点A出发以1 cm/s的速度向点C运动,同时点E从点C出发以2 cm/s的速度向点B运动,设运动的时间为t s,解决以下问题:

(1)当t为何值时,△DEC为等边三角形?

(2)当t为何值时,△DEC为直角三角形?

图 

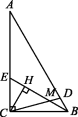
 [转化思想] 如图,在Rt△ACB中,∠ACB=90°,∠A=30°,∠ABC的平分线BE交AC于点E,D为AB上的一点,且AD=AC,CD,BE相交于点M.

(1)求∠DMB的度数;

(2)若CH⊥BE于点H,求证:AB=4MH.

图 

答案

1.C

2. D　由“在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半”可知,AC=AB.根据“直角三角形斜边上的中线等于斜边的一半”可知CD=AB=AD=BD,所以AC=AD=BD=CD.故选D.

3. C　∵∠ACB=90°,∠A=30°,AB=4,∴CB=AB=2,∠B=60°.

∵CD是AB边上的高,∴∠BDC=90°,

∴∠BCD=30°,

∴BD=BC=1.

4. B　设三个内角的度数分别为x°,(2x)°,(3x)°,则x+2x+3x=180,解得x=30,∴三个内角的度数分别为30°,60°,90°,∴这个三角形是直角三角形,30°角所对的直角边为最短边,斜边为最长边.∵这个三角形的最短边长为,∴它的最长边长为2.

5.C

6. B　∵BD⊥BC,∴∠CBD=90°,

∴∠ABD=∠ABC-∠CBD=120°-90°=30°.

∵AB=BC,∠ABC=120°,∴∠A=∠C=30°,

∴∠A=∠ABD,∴BD=AD=1.

在Rt△CBD中,∵∠C=30°,

∴CD=2BD=2.

7. A　在Rt△AEC中,∵2CE=AC,

∴∠1=30°=∠2.又∵AD=BD=4,∴∠B=∠2=30°,

∴∠ACD=90°,∴CD=AD=2.

8.5　9.30

10. 2

 ∵在△ABC中,∠C=90°,∠B=30°,∴∠CAB=60°.

∵AD平分∠CAB,∴∠CAD=∠BAD=∠CAB=30°,∴∠BAD=∠B,∴AD=BD.

∵CD=1,∠CAD=30°,∴AD=2CD=2,

∴BD=AD=2.

11. 15

 连接BD.∵DE垂直平分AB,∴AD=BD.∵AD=2BC,∴BD=2BC,∴在Rt△BCD中,∠BDC=30°.又∵BD=AD,∴∠A=∠DBA=∠BDC=15°.

12. 30°或150°

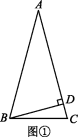
 当该三角形为锐角三角形时,如图①,

∵BD=AB,∴∠A=30°,

即△ABC的顶角为30°;

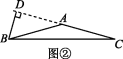
当该三角形为钝角三角形时,如图②,

在Rt△ABD中,

∵BD=AB,

∴∠BAD=30°,

∴∠BAC=150°,

即△ABC的顶角为150°.

综上所述,该等腰三角形顶角的度数为30°或150°.

13.解:∵AB⊥AC,∴∠CAB=90°.

∵AC=BC,∴∠CBA=30°.

∵AD∥BC,∴∠BAD=∠CBA=30°,

∴∠DAC=∠CAB+∠BAD=120°.

14.解:(1)证明:在△ABC中,∵∠ACB=90°,D是AB的中点,

∴CD=AD=BD=AB,

∴∠DCB=∠B.

∵∠B=30°,∠ACB=90°,

∴∠DCB=30°,∠A=90°-30°=60°,

∴∠ADC=∠B+∠DCB=60°,

∴∠A=∠ADC,∴AC=DC.

又∵CE⊥AB于点E,∴AE=DE.

(2)∵CE⊥AB,∴∠AEC=90°.

∵∠A=60°,∴∠ACE=30°,∴AE=AC.

∵AC=2,AE=DE,∴DE=AE=1.

15.解:如图,过点P作PD⊥AB,交直线AB于点D.

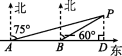
(1)由题意,得∠PBD=90°-60°=30°,∠PAB=90°-75°=15°.

∵∠PBD=∠PAB+∠APB,

∴∠APB=15°=∠PAB,

∴BP=AB=7海里.

(2)没有.理由:∵在Rt△PBD中,∠PBD=30°,

∴PD=BP=×7=3.5(海里)>3海里,

∴轮船继续向东行驶没有触礁的危险.

16.解:(1)根据题意可得AD=t cm,CD=(6-t)cm,CE=2t cm.

∵∠A=90°,∠B=30°,

∴∠C=90°-∠B=90°-30°=60°.

若△DEC为等边三角形,

则CD=CE,∴6-t=2t,解得t=2,

∴当t的值为2时,△DEC为等边三角形.

(2)①当∠DEC为直角时,∠EDC=30°,

∴CE=CD,∴2t=(6-t),解得t=;

②当∠EDC为直角时,∠DEC=30°,

∴CD=CE,∴6-t=×2t,解得t=3.

∴当t的值为或3时,△DEC为直角三角形.

[素养提升]

　　解:(1)∵∠ACB=90°,∠A=30°,

∴∠ABC=60°.

∵BE是∠ABC的平分线,

∴∠ABE=∠CBE=30°.

∵∠A=30°,AC=AD,

∴∠ACD=∠ADC=75°,

∴∠DMB=∠ADC-∠ABE=45°.

(2)证明:∵∠ACB=90°,∠A=30°,

∴AB=2BC.

∵CH⊥BE,∠CBE=30°,

∴BC=2CH,∴AB=4CH.

∵在Rt△CHM中,∠CMH=∠DMB=45°,

∴CH=MH,

∴AB=4MH.