初中数学湘教版八年级下册2.2.2平行四边形的判定综合训练题

[利用对角线的关系判定平行四边形]

一、选择题

1.四边形ABCD的对角线相交于点O,下列条件可以判定四边形ABCD是平行四边形的是(　　)

A.AC=10,BD=8

B.OA=5,OB=8,OC=5,OD=8

C.OA=5,OB=5,OC=8,OD=8

D.OA=5,OD=5,OC=8,OB=8

2.下面给出了四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的是              (　　)

A.1∶2∶3∶4  B.2∶3∶2∶3

C.2∶3∶3∶2  D.1∶2∶2∶3

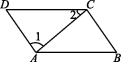
3.如图,在四边形ABCD中,对角线AC与BD相交于点O,下列不能判定四边形ABCD是平行四边形的是              (　　)

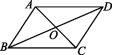
A.AB∥DC,AD=BC  B.AB∥DC,AD∥BC

C.AB=DC,AD=BC  D.OA=OC,OB=OD

二、填空题

4.将两根木条AC,BD的中点重叠,并用钉子固定,则四边形ABCD为平行四边形,理由是　　　　　　　　　　　　　　　　　. 

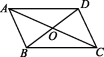
5.如图,四边形ABCD的对角线相交于点O,AO=CO,请添加一个条件:　　　　　　(填一个即可),使四边形ABCD是平行四边形. 

6.已知三条线段的长分别为10,14,20,以其中两条为对角线,其余一条为边可以画出　　　个平行四边形. 

三、解答题

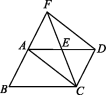
7.如图,在▱ABCD中,E是边AD的中点,连接CE并延长交BA的延长线于点F,连接AC,DF.

求证:四边形ACDF是平行四边形.

图 

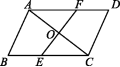
8.(2020淮安)如图,在▱ABCD中,点E,F分别在BC,AD上,AC与EF相交于点O,且AO=CO.

(1)求证:△AOF≌△COE;

(2)连接AE,CF,则四边形AECF　　　　(填“是”或“不是”)平行四边形. 

图   

9.如图,在四边形ABCD中,AB∥DC,∠B=55°,∠1=85°,∠2=40°.

(1)求∠D的度数;

(2)求证:四边形ABCD是平行四边形.

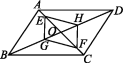
10.已知:如图,在▱ABCD中,对角线AC,BD相交于点O,点E,F在线段AC上,点G,H在线段BD上,且AE=CF,BG=DH,连接EH,HF,GF,EG.

(1)若AC=6,BD=8,试求AD的取值范围;

(2)若AC=AD,∠CAD=50°,试求∠ABC的度数;

(3)求证:四边形EHFG是平行四边形.

图   

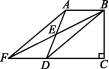
11.如图,在四边形ABCD中,AB∥CD,BC⊥CD,E是AD的中点,连接BE并延长交CD的延长线于点F.

(1)连接AF,BD,试判断四边形ABDF是何种特殊四边形,并说明理由;

(2)若AB=4,BC=5,CD=6,求△BCF的面积.

图   

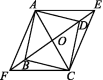
 [从特殊到一般的思想与猜想、证明] 如图,在▱ABCD中,对角线AC,BD相交于点O,OA=5 cm,E,F为直线BD上的两个动点(点E,F始终在▱ABCD的外面),当DE=OD,BF=OB时,连接AE,CE,CF,AF.据此回答下列问题:

(1)求证:四边形AFCE为平行四边形;

(2)当DE=OD,BF=OB时,其他条件不变,(1)中的结论还成立吗?由此你能得出什么结论?

(3)若CA平分∠BCD,∠AEC=60°,求四边形AFCE的周长.

答案

1.B　2.B　3.A　

4.对角线互相平分的四边形是平行四边形

5.答案不唯一,如BO=DO

6.2

7.证明:∵四边形ABCD是平行四边形,

∴AB∥CD,∴∠FAE=∠CDE.

∵E是AD的中点,∴AE=DE.

又∵∠FEA=∠CED,

∴△FAE≌△CDE(ASA),

∴FE=CE.

又∵AE=DE,

∴四边形ACDF是平行四边形.

8.解:(1)证明:∵四边形ABCD是平行四边形,

∴AD∥BC,∴∠FAO=∠ECO.

在△AOF和△COE中,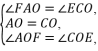

∴△AOF≌△COE(ASA).

(2)是　 由(1)知△AOF≌△COE,∴OF=OE.

又∵OA=OC,

∴四边形AECF为平行四边形.

9.解:(1)∵∠D+∠2+∠1=180°,∠1=85°,∠2=40°,

∴∠D=180°-∠2-∠1=55°.

(2)证明:∵AB∥DC,

∴∠2=∠CAB,

∴∠DAB=∠1+∠CAB=∠1+∠2=125°.

∵∠DCB+∠DAB+∠D+∠B=360°,

∴∠DCB=125°=∠DAB.

又∵∠D=∠B=55°,

∴四边形ABCD是平行四边形.

10.解:(1)∵四边形ABCD是平行四边形,

∴OA=AC=3,OD=BD=4,

∴1<AD<7.

(2)∵AC=AD,∠CAD=50°,

∴∠ADC=∠ACD=×(180°-50°)=65°.

∵四边形ABCD是平行四边形,

∴∠ABC=∠ADC=65°.

(3)证明:∵四边形ABCD是平行四边形,

∴OA=OC,OB=OD.

又∵AE=CF,BG=DH,

∴OE=OF,OG=OH,

∴四边形EHFG是平行四边形.

11.解:(1)四边形ABDF是平行四边形.

理由:∵AB∥CD,

∴∠EAB=∠EDF.

∵E是AD的中点,

∴AE=DE.

在△ABE和△DFE中,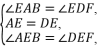

∴△ABE≌△DFE(ASA),

∴BE=FE.

又∵AE=DE,

∴四边形ABDF是平行四边形.

(2)∵△ABE≌△DFE,BC⊥CD,

∴△BCF的面积=梯形ABCD的面积=(AB+CD)·BC=×(4+6)×5=25.

[素养提升]

解:(1)证明:∵四边形ABCD是平行四边形,

∴OA=OC,OB=OD.

∵DE=OD,BF=OB,且F,B,D,E四点共线,∴DE=BF,

∴OE=OF.

又∵OA=OC,

∴四边形AFCE为平行四边形.

(2)成立.理由:∵四边形ABCD是平行四边形,

∴OA=OC,OB=OD.

∵DE=OD,BF=OB,∴DE=BF,

∴OE=OF.

又∵OA=OC,

∴四边形AFCE为平行四边形.

由此可得出结论:若DE=OD,BF=OB(n>0),则四边形AFCE为平行四边形.

(3)∵四边形ABCD为平行四边形,

∴AD∥BC,

∴∠DAC=∠BCA.

∵CA平分∠BCD,

∴∠BCA=∠DCA,

∴∠DCA=∠DAC,∴AD=CD.

∵OA=OC,∴OD⊥AC,

∴OE是线段AC的垂直平分线,

∴AE=CE.

∵∠AEC=60°,

∴△ACE是等边三角形,

∴AE=CE=AC=2OA=10 cm,

∴四边形AFCE的周长=2(AE+CE)=2×(10+10)=40(cm).