初中数学2.2.2平行四边形的判定课后测评

这是一份初中数学2.2.2平行四边形的判定课后测评，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
[利用边的关系判定平行四边形]一、选择题1.下列条件能判定四边形ABCD是平行四边形的是 (　　)A.∠A+∠B=180°,∠C+∠D=180°B.∠A+∠B=180°,∠C+∠A=180°C.∠A+∠D=180°,∠C+∠B=180°D.∠A+∠D=180°,∠A+∠B=180°2.已知在四边形ABCD中,AB∥CD,若要用“一组对边平行且相等的四边形是平行四边形”判定四边形ABCD是平行四边形,还需要添加的条件是(　　)A.AD=BC B.AC=BD C.AB=CD D.AB=AD3.在四边形ABCD中,若AB=3,BC=4,CD=3,要使该四边形是平行四边形,则AD的长是 (　　)A.3 B.4 C.5 D.6二、填空题4.如图,A是直线l外一点,在l上取两点B,C,分别以点A,C为圆心,BC,AB的长为半径画弧,两弧交于点D,分别连接AB,AD,CD,则四边形ABCD一定是　　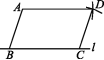　　　. 5.在四边形ABCD中,AD=BC,要使四边形ABCD是平行四边形,还需添加一个条件,这个条件可以是　　　　　　.(写出一种情况即可) 6.一个四边形的四条边长依次为a,b,c,d,且满足(a-c)2+(b-d)2=0,则这个四边形一定是　　　　　. 三、解答题7.已知:如图,在▱ABCD中,E,F分别是边AD,BC的中点.求证:四边形BFDE是平行四边形.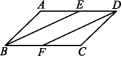图        8.证明命题:若四边形ABCD和四边形BEFC都是平行四边形,则四边形AEFD是平行四边形.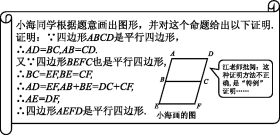请指出小海同学证明过程中的错误之处,并写出你的证明过程.     9.如图,在线段AD上有E,F两点,且AE=DF,过点E,F分别作AD的垂线BE和CF,连接AB,CD,BF,CE,且AB∥CD.求证:四边形BECF是平行四边形. 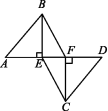  10.如图,已知∠A=∠D,AB=DC,AC,BD相交于点O.(1)求证:△AOB≌△DOC;(2)若AB=BC,∠A=32°,求∠AOB的度数;(3)作△BDC关于直线BC的对称图形△BEC,求证:四边形ABEC是平行四边形.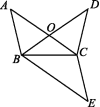图      [分类讨论思想] 如图,等边三角形ABC的边长为8,动点M从点B出发,沿B→A→C→B的方向以每秒3个单位的速度运动,动点N从点C出发,沿C→A→B→C的方向以每秒2个单位的速度运动.(1)若动点M,N同时出发,经过几秒第一次相遇?(2)若动点M,N同时出发,且其中一点到达终点时,另一点立即停止运动.在△ABC的边上是否存在一点D,使得以点A,M,N,D为顶点的四边形为平行四边形?若存在,求此时运动的时间t及点D的具体位置;若不存在,请说明理由.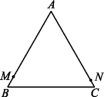  
答案1.D　2.C　3.B4. 平行四边形 ∵分别以点A,C为圆心,BC,AB的长为半径画弧,两弧交于点D,∴AD=BC,AB=CD,∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).5.答案不唯一,如AB=CD6. 平行四边形 ∵(a-c)2+(b-d)2=0,∴a=c,b=d,∴四边形ABCD是平行四边形.7.证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.∵E,F分别是边AD,BC的中点,∴DE=BF.又∵DE∥BF,∴四边形BFDE是平行四边形.8.解:小海同学证明过程中的错误之处是列举了一个特例,画出了特殊图形,应该画一般图形.证明:如图.∵四边形ABCD和四边形BEFC都是平行四边形,∴AD∥BC,AD=BC,BC∥EF,BC=EF,∴AD∥EF,AD=EF,∴四边形AEFD是平行四边形.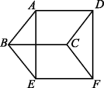9.证明:∵BE⊥AD,CF⊥AD,∴∠AEB=∠BEF=∠CFE=∠DFC=90°,∴BE∥CF.∵AB∥CD,∴∠A=∠D.在△AEB和△DFC中,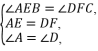∴△AEB≌△DFC(ASA),∴BE=CF.又∵BE∥CF,∴四边形BECF是平行四边形.10.解:(1)证明:在△AOB与△DOC中,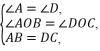∴△AOB≌△DOC(AAS).(2)∵AB=BC,∠A=32°,∴∠ACB=∠A=32°.∵△AOB≌△DOC,∴OB=OC,∴∠OCB=∠OBC=32°,∴∠AOB=∠OCB+∠OBC=64°.(3)证明:在△ABC与△DCB中,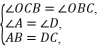∴△ABC≌△DCB,∴AC=DB.∵△BDC与△BEC关于直线BC对称,∴DC=CE,DB=BE,∴AB=CE,AC=BE,∴四边形ABEC是平行四边形.[素养提升]解:(1)设动点M,N同时出发,经过x秒第一次相遇.由题意,得3x+2x=16,解得x=.即动点M,N同时出发,经过秒第一次相遇.(2)存在.①当0≤t≤时,点M,N,D的位置如图(a)所示.∵四边形ANDM为平行四边形,∴AM=ND,AM∥ND,∴∠NDC=∠B.∵△ABC为等边三角形,∴∠B=∠C=60°,∴∠NDC=∠C,∴ND=NC,∴AM=NC,∴MA+BM=NC+BM=8,即2t+3t=8,解得t=,此时点D在线段BC上,且BD=或CD=.②当<t≤4时,A,M,N三点在同一直线上,不能构成平行四边形.③当4<t≤时,点M,N,D的位置如图(b)所示.∵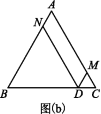四边形ANDM为平行四边形,∴ND=AM,AM∥ND,∴∠NDB=∠C.∵△ABC为等边三角形,∴∠B=∠C=60°,∴∠NDB=∠B,∴ND=NB,∴AM=NB,∴AM+AN=NB+AN=8,即3t-8+2t-8=8,解得t=,此时点D在线段BC上,且BD=或CD=.④当<t≤8时,点M,N,D的位置如图(c)所示.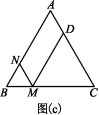由题意得BN=16-2t,BM=24-3t.易得△BNM为等边三角形,∴BN=BM,即16-2t=24-3t,解得t=8,此时点M,N重合,不能构成平行四边形.故在△ABC的边上存在一点D,使得以点A,M,N,D为顶点的四边形为平行四边形,此时运动的时间t为秒或秒,此时点D在线段BC上,分别为BD=或CD=,BD=或CD=.