湘教版八年级下册1.2 直角三角形的性质与判定（Ⅱ）课后练习题

这是一份湘教版八年级下册1.2 直角三角形的性质与判定（Ⅱ）课后练习题，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
[勾股定理]一、选择题1.如图,在Rt△ABC中,∠C=90°,AB=2,AC=1,则BC的长度为 (　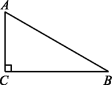　)A.5 B.3 C. D.2.如图,在边长为1的小正方形组成的网格中,点A,B都在格点上,则线段AB的长度为(　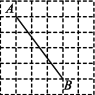　)A.5　 B.6　 C.7　 D.253.如图,所有的四边形都是正方形,三角形为直角三角形,若正方形A,B的面积分别为5,3,则正方形C的面积是   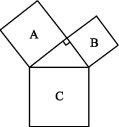           (　　)A.15 B.13 C.11 D.8 4.如图,在△ABC中,AD是∠BAC的平分线,已知AB=AC=13,AD=12,则BC的长为 (　　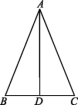)A.5 B.8 C.9 D.105.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形中较长的直角边长为a,较短的直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为   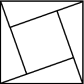           (　　)A.9 B.6 C.4 D.36.如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2……依此法继续作下去,得OP2022等于  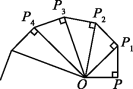            (　　)A.  B.C.  D.二、填空题7.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若AC=3,BC=4,则DC=　　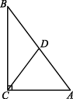　　. 8.如图,在△ABC中,CD⊥AB于点D,E是AC的中点.若AD=6,DE=5,则CD=　　　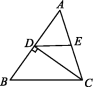　. 9.在Rt△ABC中,∠C=90°,AB=15,BC∶AC=3∶4,则BC=　　　　. 10.若直角三角形的两边长分别为6和8,则该三角形的第三边长为　　　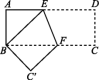　　. 11.在长方形纸片ABCD中,AD=10 cm,AB=4 cm,按图所示的方式折叠,使点D与点B重合,点C落在点C'处,折痕为EF,则DE=　　　　 cm. 12.(2021永州蓝山县期末)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,若AC=12,BC=5,则CD=　　　　. 13.如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边向外作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2……按照此规律继续下去,则S2022的值为　　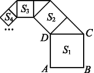　　. 三、解答题14.如图,在△ABC中,AB=13,BC=21,AD⊥BC,垂足为D,AD=12,求AC的长. 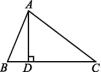   15.如图,折叠长方形纸片ABCD的一边AD,使点D落在BC边上的点F处,已知AB=CD=8 cm,BC=AD=10 cm,求EC的长. 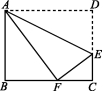   16.如图,在△ABC中,∠B=90°,AB=16 cm,AC=20 cm,P,Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为1 cm/s,点Q从点B开始沿B→C→A方向运动,且速度为2 cm/s,它们同时出发,设运动的时间为t s.(1)求BC的长;(2)当t为何值时,点P在边AC的垂直平分线上?求出此时CQ的长.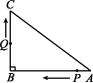   含45°角的三角尺按如图所示方式放置,直角顶点C在直线m上,分别过点A,B作AE⊥直线m于点E,BD⊥直线m于点D.(1)求证:EC=BD;(2)若设△AEC的三边长分别为a,b,c,利用此图证明勾股定理.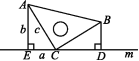 
答案1.D2. A　如图,AB==5.故选A.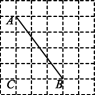3. D　设正方形A,B,C的边长分别为x,y,z,由勾股定理,得z2=x2+y2=5+3=8,∴正方形C的面积为8.4.D5. D　设直角三角形的斜边长为c.根据勾股定理,得c2=a2+b2.∵大正方形的面积为25,∴c2=25,即a2+b2=25.∵ab=8,∴(a-b)2=a2+b2-2ab=25-2×8=9,即a-b=3,即小正方形的边长为3.6. D　由OP=1,OP1=,OP2=,OP3=,OP4==,…,可得OPn=,∴OP2022=.7.2.58. 8 因为CD⊥AB于点D,E是AC的中点,且DE=5,所以AC=10.在Rt△ADC中,CD===8.9.910.10或211.　12.13.  如图所示.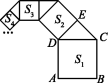∵正方形ABCD的边长为2,△CDE为等腰直角三角形,∴DE2+CE2=CD2,DE=CE,∴S2+S2=S1.观察,发现规律:S1=22=4,S2=S1=2,S3=S2=2S1=1,S4=S3=3S1=,…,∴S2022=2022-1S1=.14.解:∵AD⊥BC,∴∠ADB=∠ADC=90°.∵AB=13,AD=12,∴BD===5.∵BC=21,∴CD=BC-BD=16,∴AC===20.15.解:依题意,可得BC=AD=AF=10 cm,DE=EF.在△ABF中,∠ABF=90°,∴BF===6(cm),∴FC=10-6=4(cm).设EC=x cm,则EF=DE=(8-x)cm.∵在△EFC中,∠C=90°,∴EC2+FC2=EF2,即x2+42=(8-x)2,解得x=3,∴EC=3 cm.16.解:(1)∵∠B=90°,AB=16 cm,AC=20 cm,∴BC===12(cm).(2)∵点P在边AC的垂直平分线上,∴PC=PA=t cm,PB=(16-t)cm.在Rt△BPC中,BC2+PB2=PC2,即122+(16-t)2=t2,解得t=,∴当t=时,点P在边AC的垂直平分线上.此时,点Q运动的路程为2×=25(cm)>12 cm,∴点Q在边AC上,∴CQ=25-12=13(cm).[素养提升]证明:(1)∵△ABC是等腰直角三角形,∴∠ACB=90°,AC=BC,∴∠ACE+∠BCD=90°.∵AE⊥EC,BD⊥CD,∴∠AEC=∠CDB=90°,∴∠CAE+∠ACE=90°,∴∠CAE=∠BCD,∴△AEC≌△CDB(AAS),∴EC=BD.(2)∵△AEC≌△CDB,△AEC的三边长分别为a,b,c,∴BD=EC=a,CD=AE=b,BC=AC=c,∴S梯形=(AE+BD)·ED=(a+b)(a+b),S梯形=S△AEC+S△ABC+S△CDB=ab+c2+ab,∴(a+b)(a+b)=ab+c2+ab,整理可得a2+b2=c2,故勾股定理得证.