人教版初中数学九年级上册 第23章《旋转 小结与复习》课件+教案+同步检测（含教学反思）

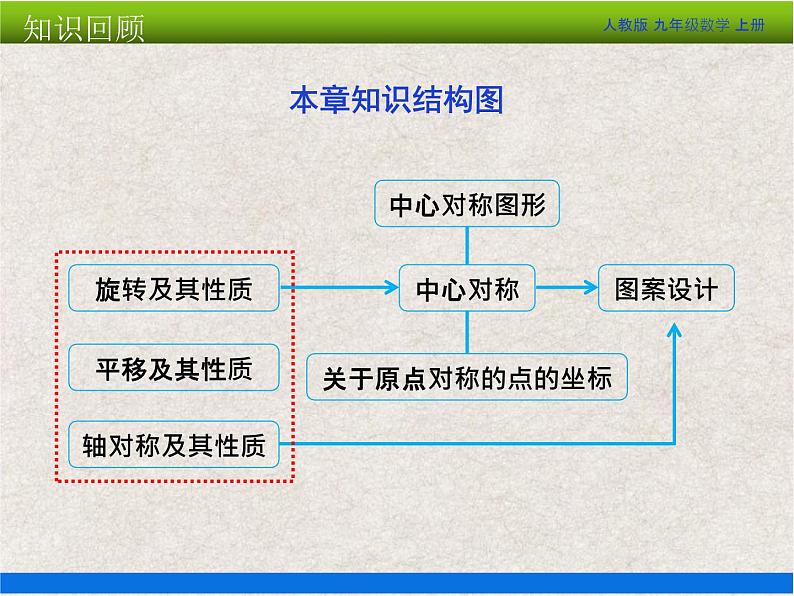
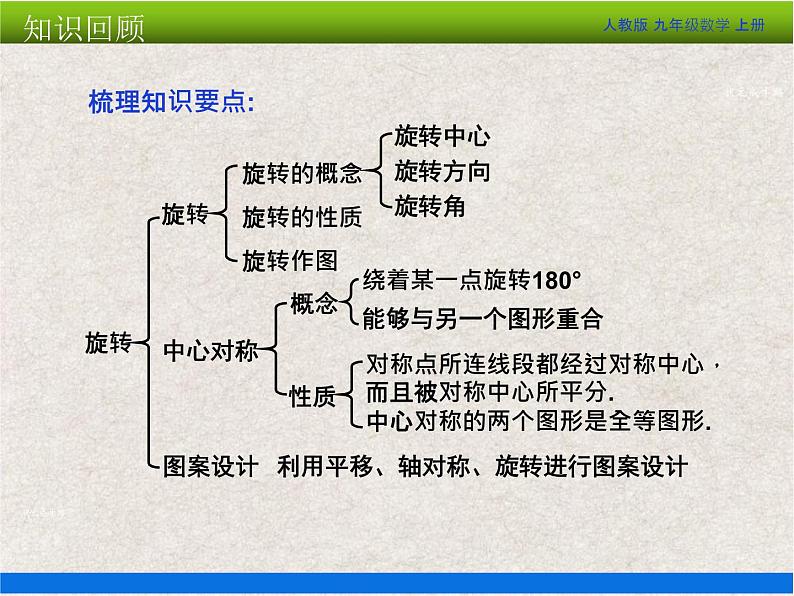
第23章 旋转（单元测试）

一、单选题（每题3分，共30分）

1．下列图形既是轴对称图形，又是中心对称图形的是（    ）

A．B．C． D．

2．若点与点关于原点成中心对称，则的值是（　　）

A．1 B．3 C．5 D．7

3．以原点为中心，将点P（4，5）按逆时针方向旋转90°，得到的点Q所在的象限为（　　）

A．第一象限 B．第二象限 C．第三象限 D．第四象限

4．把一副三角板按如图放置，其中∠ABC=∠DEB=90°，∠A=45°，∠D=30°，斜边AC=BD=10，若将三角板DEB绕点B逆时针旋转45°得到△D′E′B，则点A在△D′E′B的（ ）

A．内部 B．外部 C．边上 D．以上都有可能

5．二次函数的图象的顶点坐标是，且图象与轴交于点．将二次函数的图象以原点为旋转中心顺时针旋转180°，则旋转后得到的函数解析式为（    ）

A． B．

C． D．

6．如图，等边三角形ABC内有一点P，分别连结AP、BP、CP，若AP＝6，BP＝8，CP＝10．则S△ABP+S△BPC＝（   ）．

A．20+16 B．24+12 C．20+12 D．24+16

7．时钟上的分针匀速旋转一周需要 60min，则经过 5min，分针旋转了（     ）

A．10° B．20° C．30° D．60°

8．如图，在正方形网格中有两个小正方形被涂黑，再将图中其余小正方形涂黑一个，使得整个黑色图形构成一个轴对称图形．那么涂法共有（    ）

A．3种 B．4种 C．5种 D．6种

9．在下面的网格图中，每个小正方形的边长均为1，△ABC的三个顶点都是网格线的交点，已知B，C两点的坐标分别为（﹣1，﹣1），（1，﹣2），将△ABC绕点C顺时针旋转90°，则点A的对应点的坐标为（   ）

A．（4，1） B．（4，﹣1） C．（5，1） D．（5，﹣1）

10．Rt△ABC中，AB=AC，点D为BC中点．∠MDN=90°，∠MDN绕点D旋转，DM、DN分别与边AB、AC交于E、F两点．下列结论

①(BE+CF)=BC，②，③AD·EF，④AD≥EF，⑤AD与EF可能互相平分，

其中正确结论的个数是（    ）

A．1个 B．2个 C．3个 D．4个

二、填空题（每题4分，共20分）

11．如图，已知点A(2，0)，B(0，4)，C(2，4)，D(6，6)，连接AB，CD，将线段AB绕着某一点旋转一定角度，使其与线段CD重合（点A与点C重合，点B与点D重合），则这个旋转中心的坐标为     ．

12．如图，在△ABC中，∠BAC=90°，AB=AC=10cm，点D为△ABC内一点，∠BAD=15°，AD=6cm，连接BD，将△ABD绕点A逆时针方向旋转，使AB与AC重合，点D的对应点E，连接DE，DE交AC于点F，则CF的长为        cm.

13．对于下列图形：①等边三角形； ②矩形； ③平行四边形； ④菱形； ⑤正八边形；⑥圆．其中既是轴对称图形，又是中心对称图形的是     ．（填写图形的相应编号）

14．如图，在平面直角坐标系中，将△ABO绕点A顺指针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去……，若点A(，0)，B(0，4)，则点B2019的横坐标为     ．

15．如图所示，两个边长都为4cm的正方形ABCD和正方形OEFG，O是正方形ABCD的对称中心，则图中阴影部分的面积为       cm2．

三、解答题（16-18题每题4分，19题5分，20题7分，21、22题每题8分，23题10分，共50分）

16．如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．

(1) 请画出△ABC向左平移5个单位长度后得到的△ABC；

(2) 请画出△ABC关于原点对称的△ABC；

(3) 在轴上求作一点P，使△PAB的周长最小，请画出△PAB，

并直接写出P的坐标．

17．图1，图2都是由边长为1的小等边三角形构成的网格，每个网格图中有3个小等边三角形已涂上阴影．请在余下的空白小等边三角形中，分别按下列要求选取一个涂上阴影：

（1）使得4个阴影小等边三角形组成一个轴对称图形．

（2）使得4个阴影小等边三角形组成一个中心对称图形．（请将两个小题依次作答在图1，图2中，均只需画出符合条件的一种情形）

18．如图，将△OAB绕点O逆时针旋转80°得到△OCD，点A与点C是对应点．

（1）画出△OAB关于点O对称的图形（保留画图痕迹，不写画法）；

（2）若∠A=110°，∠D=40°，求∠AOD的度数．

19．（1）指出下列旋转对称图形的最小旋转角，并在图中标明它的旋转中心O．

（2）在上述几个图形中有没有中心对称图形？具体指明是哪几个？

解：图形A的最小旋转角是　 　度，它　 　中心对称图形．

图形B的最小旋转角是　 　度，它　 　中心对称图形．

图形C的最小旋转角是　 　度，它　 　中心对称图形．

图形D的最小旋转角是　 　度，它　 　中心对称图形．

图形E的最小旋转角是　 　度，它　 　中心对称图形．

20．如图，在矩形ABCD中，对角线AC的中点为O，点G，H在对角线AC上，AG＝CH，直线GH绕点O逆时针旋转α角，与边AB、CD分别相交于点E、F（点E不与点A、B重合）．

（1）求证：四边形EHFG是平行四边形；

（2）若∠α＝90°，AB＝9，AD＝3，求AE的长．

21．在Rt△ABC中，∠ACB=90°，AC=BC=3，点D是斜边AB上一动点（点D与点A、B不重合），连接CD，将CD绕点C顺时针旋转90°得到CE，连接AE，DE．

（1）求△ADE的周长的最小值；

（2）若CD=4，求AE的长度．

22．如图，是等边三角形内一点，将线段绕点顺时针旋转60°得到线段，连接，，．若，，，求四边形的面积．

23．已知和都是等腰直角三角形，．

（1）如图1，连接，，求证：；

（2）将绕点O顺时针旋转．

①如图2，当点M恰好在边上时，求证：；

②当点A，M，N在同一条直线上时，若，，请直接写出线段的长．