


江西省信丰县2022-2023学年数学七下期末综合测试试题含答案
展开
这是一份江西省信丰县2022-2023学年数学七下期末综合测试试题含答案,共7页。试卷主要包含了已知实数满足,则代数式的值是,一个正比例函数的图象经过等内容,欢迎下载使用。
江西省信丰县2022-2023学年数学七下期末综合测试试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1.已知二次函数![]() (a≠0)的图象的顶点在第四象限,且过点(﹣1,0),当a﹣b为整数时,ab的值为( )A.
(a≠0)的图象的顶点在第四象限,且过点(﹣1,0),当a﹣b为整数时,ab的值为( )A.![]() 或1 B.
或1 B.![]() 或1 C.
或1 C.![]() 或
或![]() D.
D.![]() 或
或![]() 2.某天,小明走路去学校,开始他以较慢的速度匀速前进,然后他越走越快走了一段时间,最后他以较快的速度匀速前进达到学校.小明走路的速度v(米/分钟)是时间t(分钟)的函数,能正确反映这一函数关系的大致图像是( )A.
2.某天,小明走路去学校,开始他以较慢的速度匀速前进,然后他越走越快走了一段时间,最后他以较快的速度匀速前进达到学校.小明走路的速度v(米/分钟)是时间t(分钟)的函数,能正确反映这一函数关系的大致图像是( )A.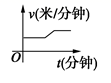 B.
B.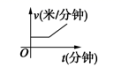 C.
C.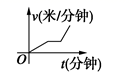 D.
D.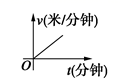 3.下列计算中,运算错误的是( )A.
3.下列计算中,运算错误的是( )A.![]() B.
B.![]() C.
C.![]() D.(-
D.(-![]() )2=34.已知正多边形的一个内角是140°,则这个正多边形的边数是( )A.九边形 B.八边形 C.七边形 D.六边形5.数据2,3,3,5,6,10,13的中位数为( )A.5 B.4 C.3 D.66.已知实数
)2=34.已知正多边形的一个内角是140°,则这个正多边形的边数是( )A.九边形 B.八边形 C.七边形 D.六边形5.数据2,3,3,5,6,10,13的中位数为( )A.5 B.4 C.3 D.66.已知实数![]() 满足
满足![]() ,则代数式
,则代数式![]() 的值是( )A.7 B.-1 C.7或-1 D.-5或37.在△ABC中,AB=
的值是( )A.7 B.-1 C.7或-1 D.-5或37.在△ABC中,AB=![]() ,BC=
,BC=![]() ,AC=
,AC=![]() ,则( )A.∠A=90° B.∠B=90° C.∠C=90° D.∠A=∠B8.一个正比例函数的图象经过(1,﹣3),则它的表达式为( )A.y=﹣3x B.y=3x C.y=
,则( )A.∠A=90° B.∠B=90° C.∠C=90° D.∠A=∠B8.一个正比例函数的图象经过(1,﹣3),则它的表达式为( )A.y=﹣3x B.y=3x C.y=![]() D.y=﹣
D.y=﹣![]() 9.如图,在
9.如图,在![]() 中,
中,![]() ,
,![]() ,点D,E分别是AB, BC的中点,连接DE,CD,如果
,点D,E分别是AB, BC的中点,连接DE,CD,如果![]() ,那么
,那么![]() 的周长( )
的周长( )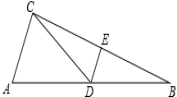 A.28 B.28.5 C.32 D.3610.已知一次函数
A.28 B.28.5 C.32 D.3610.已知一次函数![]() 不过第二象限,则b试问取值范围是( )A.b<0 B.b>0 C.b≤0 D.b≥0二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,
不过第二象限,则b试问取值范围是( )A.b<0 B.b>0 C.b≤0 D.b≥0二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,![]() 的对角线
的对角线![]() ,
,![]() 交于点
交于点![]() ,点
,点![]() 是
是![]() 的中点,若
的中点,若![]() ,则
,则![]() 的长是______.
的长是______.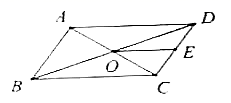 12.若次函数y=(a﹣1)x+a﹣8的图象经过第一,三,四象限,且关于y的分式方程
12.若次函数y=(a﹣1)x+a﹣8的图象经过第一,三,四象限,且关于y的分式方程![]() 有整数解,则满足条件的整数a的值之和为_____.13.端午节那天,“味美早餐店”的粽子打9折出售,小红的妈妈去该店买粽子花了54元钱,比平时多买了3个,则平时每个粽子卖_____元.14.方程
有整数解,则满足条件的整数a的值之和为_____.13.端午节那天,“味美早餐店”的粽子打9折出售,小红的妈妈去该店买粽子花了54元钱,比平时多买了3个,则平时每个粽子卖_____元.14.方程![]() 的解为__________.15.如图,小明想利用太阳光测量楼高,发现对面墙上有这栋楼的影子,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠且高度恰好相同.此时测得墙上影子高
的解为__________.15.如图,小明想利用太阳光测量楼高,发现对面墙上有这栋楼的影子,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠且高度恰好相同.此时测得墙上影子高![]() ,
,![]() ,
,![]() (点A、E、C在同一直线上).已知小明身高EF是1.6m,则楼高AB为______m.
(点A、E、C在同一直线上).已知小明身高EF是1.6m,则楼高AB为______m.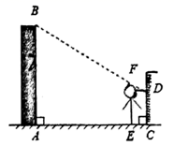 16.如图,正方形ABCD的边长为a,E是AB的中点,CF平分∠DCE,交AD于F,则AF的长为______.
16.如图,正方形ABCD的边长为a,E是AB的中点,CF平分∠DCE,交AD于F,则AF的长为______.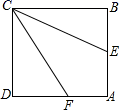 三、解下列各题(本大题共8小题,共72分)17.(8分)为缓解油价上涨给出租车待业带来的成本压力,某巿自2018年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数) 行驶路程收费标准调价前调价后不超过3km的部分起步价6元起步价a 元超过3km不超出6km的部分每公里2.1元每公里b元超出6km的部分每公里c元设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元)如图,折线ABCD表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:(1)填空:a= ,b= ,c= .(2)写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.(3)函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义,若不存在请说明理由.
三、解下列各题(本大题共8小题,共72分)17.(8分)为缓解油价上涨给出租车待业带来的成本压力,某巿自2018年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数) 行驶路程收费标准调价前调价后不超过3km的部分起步价6元起步价a 元超过3km不超出6km的部分每公里2.1元每公里b元超出6km的部分每公里c元设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元)如图,折线ABCD表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:(1)填空:a= ,b= ,c= .(2)写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.(3)函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义,若不存在请说明理由.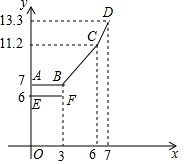 18.(8分)如图,在四边形ABCD中,AB=BC=3,CD=
18.(8分)如图,在四边形ABCD中,AB=BC=3,CD=![]() ,DA=5,∠B=90°,求∠BCD的度数
,DA=5,∠B=90°,求∠BCD的度数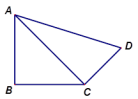 19.(8分)如图,在平面直角坐标系
19.(8分)如图,在平面直角坐标系![]() 中,
中,![]() 的直角边
的直角边![]() 在
在![]() 轴上,
轴上,![]() .点
.点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() 是
是![]() 边的中点,函数
边的中点,函数![]() 的图象经过点
的图象经过点![]() .
.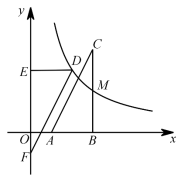 (1)求
(1)求![]() 的值;(2)将
的值;(2)将![]() 绕某个点旋转
绕某个点旋转![]() 后得到
后得到![]() (点
(点 ![]() ,
,![]() ,
,![]() 的对应点分别为点
的对应点分别为点![]() ,
,![]() ,
,![]() ),且
),且 ![]() 在
在![]() 轴上,点
轴上,点![]() 在函数
在函数![]() 的图象上,求直线
的图象上,求直线![]() 的表达式. 20.(8分)计算下列各题:(1)
的表达式. 20.(8分)计算下列各题:(1)![]() ;(2)
;(2)![]() . 21.(8分)解方程:(1)
. 21.(8分)解方程:(1)![]() ;(2)甲、乙两公司为“见义勇为基金会”各捐款3000元.已知甲公司的人数比乙公司的人数多20%,乙公司比甲公司人均多捐20元.求甲、乙两公司各有多少人? 22.(10分)某开发公司生产的960件新产品,需要精加工后,才能投放市场.现有甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工完这批产品比乙工厂单独加工完这批产品多用20天,而乙工厂每天比甲工厂多加工8件产品,公司需付甲工厂加工费用每天80元,乙工厂加工费用每天120元.(1)求甲、乙两个工厂每天各能加工多少件新产品.(2)公司制定产品加工方案如下:可以由每个厂家单独完成;也可以由两个厂家同时合作完成.在加工过程中,公司需派一名工程师每天到厂进行技术指导,并负担每天5元的误餐补助费. 请你帮助公司选择一种既省时又省钱的加工方案,并说明理由. 23.(10分)在校园手工制作活动中,甲、乙两人接到手工制作纸花任务,已知甲每小时制作纸花比乙每小时制作纸花少20朵,甲制作120朵纸花的时间与乙制作160朵纸花的时间相同(1)求甲、乙两人每小时各制作纸花多少朵?(2)本次活动学校需要该种纸花不少于350朵,若由甲、乙两人共同制作,则至少需要几小时完成任务? 24.(12分)如图1,平面直角坐标系中,直线AB:y=﹣
;(2)甲、乙两公司为“见义勇为基金会”各捐款3000元.已知甲公司的人数比乙公司的人数多20%,乙公司比甲公司人均多捐20元.求甲、乙两公司各有多少人? 22.(10分)某开发公司生产的960件新产品,需要精加工后,才能投放市场.现有甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工完这批产品比乙工厂单独加工完这批产品多用20天,而乙工厂每天比甲工厂多加工8件产品,公司需付甲工厂加工费用每天80元,乙工厂加工费用每天120元.(1)求甲、乙两个工厂每天各能加工多少件新产品.(2)公司制定产品加工方案如下:可以由每个厂家单独完成;也可以由两个厂家同时合作完成.在加工过程中,公司需派一名工程师每天到厂进行技术指导,并负担每天5元的误餐补助费. 请你帮助公司选择一种既省时又省钱的加工方案,并说明理由. 23.(10分)在校园手工制作活动中,甲、乙两人接到手工制作纸花任务,已知甲每小时制作纸花比乙每小时制作纸花少20朵,甲制作120朵纸花的时间与乙制作160朵纸花的时间相同(1)求甲、乙两人每小时各制作纸花多少朵?(2)本次活动学校需要该种纸花不少于350朵,若由甲、乙两人共同制作,则至少需要几小时完成任务? 24.(12分)如图1,平面直角坐标系中,直线AB:y=﹣![]() x+b交x轴于点A(8,0),交y轴正半轴于点B.(1)求点B的坐标;(2)如图2,直线AC交y轴负半轴于点C,AB=BC,P为线段AB上一点,过点P作y轴的平行线交直线AC于点Q,设点P的横坐标为t,线段PQ的长为d,求d与t之间的函数关系式;(3)在(2)的条件下,M为CA延长线上一点,且AM=CQ,在直线AC上方的直线AB上是否存在点N,使△QMN是以QM为斜边的等腰直角三角形?若存在,请求出点N的坐标及PN的长度;若不存在,请说明理由.
x+b交x轴于点A(8,0),交y轴正半轴于点B.(1)求点B的坐标;(2)如图2,直线AC交y轴负半轴于点C,AB=BC,P为线段AB上一点,过点P作y轴的平行线交直线AC于点Q,设点P的横坐标为t,线段PQ的长为d,求d与t之间的函数关系式;(3)在(2)的条件下,M为CA延长线上一点,且AM=CQ,在直线AC上方的直线AB上是否存在点N,使△QMN是以QM为斜边的等腰直角三角形?若存在,请求出点N的坐标及PN的长度;若不存在,请说明理由.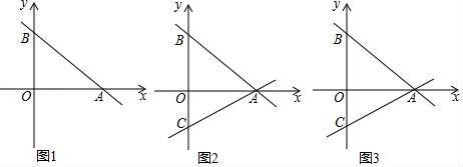 参考答案 一、选择题(每小题3分,共30分)1、A2、A3、C4、A5、A6、A7、A8、A9、C10、C 二、填空题(本大题共有6小题,每小题3分,共18分)11、312、113、214、015、21.216、
参考答案 一、选择题(每小题3分,共30分)1、A2、A3、C4、A5、A6、A7、A8、A9、C10、C 二、填空题(本大题共有6小题,每小题3分,共18分)11、312、113、214、015、21.216、![]() a 三、解下列各题(本大题共8小题,共72分)17、(1)7,1.4,2.1;(2)y1=2.1x﹣0.3;图象见解析;(3)函数y1与y2的图象存在交点(
a 三、解下列各题(本大题共8小题,共72分)17、(1)7,1.4,2.1;(2)y1=2.1x﹣0.3;图象见解析;(3)函数y1与y2的图象存在交点(![]() ,9);其意义为当 x<
,9);其意义为当 x<![]() 时是方案调价前合算,当x>
时是方案调价前合算,当x>![]() 时方案调价后合算.18、135°.19、(1)5;(4)y=4x-1.20、(1)
时方案调价后合算.18、135°.19、(1)5;(4)y=4x-1.20、(1)![]() ;(2)
;(2)![]() .21、(1)
.21、(1)![]() ,
,![]() ;(2)甲公司有1名员工,乙公司有25名员工.22、 (1)甲、乙两个工厂每天各能加工16和24件.(2)合作.23、 (1)甲每小时制作纸花60朵,每小时制作纸花80朵;(2)至少需要2.5小时完成任务.24、 (1) B(0,6);(2) d=﹣
;(2)甲公司有1名员工,乙公司有25名员工.22、 (1)甲、乙两个工厂每天各能加工16和24件.(2)合作.23、 (1)甲每小时制作纸花60朵,每小时制作纸花80朵;(2)至少需要2.5小时完成任务.24、 (1) B(0,6);(2) d=﹣![]() t+10;(3)见解析.
t+10;(3)见解析.
相关试卷
这是一份2023-2024学年江西省赣州市信丰县九上数学期末考试试题含答案,共7页。
这是一份2023-2024学年江西省信丰县数学九上期末质量跟踪监视试题含答案,共8页。试卷主要包含了下列函数中,图象不经过点,下列各组图形中,一定相似的是等内容,欢迎下载使用。
这是一份2023-2024学年江西省赣州市信丰县八上数学期末达标检测试题含答案,共7页。试卷主要包含了答题时请按要求用笔,下列各点中,位于第二象限的是,下列运算中,结果正确的是等内容,欢迎下载使用。








