

江西省育华学校2022-2023学年七年级数学第二学期期末达标检测模拟试题含答案
展开
这是一份江西省育华学校2022-2023学年七年级数学第二学期期末达标检测模拟试题含答案,共7页。试卷主要包含了在下列命题中,是假命题的个数有等内容,欢迎下载使用。
江西省育华学校2022-2023学年七年级数学第二学期期末达标检测模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1.下表记录了四名运动员参加男子跳高选拔赛成绩的平均数![]() 与方差
与方差![]() : 甲乙丙丁平均数
: 甲乙丙丁平均数![]() 173175175174方差
173175175174方差![]() 3.53.512.515如果选一名运动员参加比赛,应选择( )A.甲 B.乙 C.丙 D.丁2.如图,▱ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=
3.53.512.515如果选一名运动员参加比赛,应选择( )A.甲 B.乙 C.丙 D.丁2.如图,▱ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②S▱ABCD=AB•AC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②S▱ABCD=AB•AC;③OB=AB;④OE=![]() BC,成立的个数有()
BC,成立的个数有() A.1个B.2个C.3个D.4个3.若分式
A.1个B.2个C.3个D.4个3.若分式![]() 有意义,则
有意义,则![]() 的取值范围是
的取值范围是![]()
![]() A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.如图,
4.如图,![]() 分别是
分别是![]() 的边
的边![]() 上的点,
上的点,![]() 将四边形
将四边形![]() 沿
沿![]() 翻折,得到
翻折,得到![]() 交
交![]() 于点
于点![]() 则
则![]() 的周长为( )
的周长为( )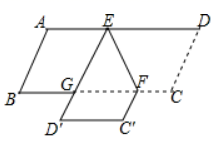 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.在下列命题中,是假命题的个数有( )①如果
5.在下列命题中,是假命题的个数有( )①如果![]() ,那么
,那么![]() . ② 两条直线被第三条直线所截,同位角相等③面积相等的两个三角形全等 ④ 三角形的一个外角等于不相邻的两个内角的和.A.3个 B.2个 C.1个 D.0个6.醴陵市“师生诗词大赛”成绩结果统计如表,成绩在91--100分的为优秀,则优秀的频率是( )分数段61--7071--8081--9091--100人数(人)2864A.0.2 B.0.25 C.0.3 D.0.357.若
. ② 两条直线被第三条直线所截,同位角相等③面积相等的两个三角形全等 ④ 三角形的一个外角等于不相邻的两个内角的和.A.3个 B.2个 C.1个 D.0个6.醴陵市“师生诗词大赛”成绩结果统计如表,成绩在91--100分的为优秀,则优秀的频率是( )分数段61--7071--8081--9091--100人数(人)2864A.0.2 B.0.25 C.0.3 D.0.357.若![]() 是三角形的三边长,则式子
是三角形的三边长,则式子![]() 的值( ).A.小于0 B.等于0 C.大于0 D.不能确定8.如图,在
的值( ).A.小于0 B.等于0 C.大于0 D.不能确定8.如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 上的点,
上的点,![]() ∥
∥![]() 交
交![]() 于点
于点![]() ,
,![]() ∥
∥![]() 交
交![]() 于点
于点![]() ,那么四边形
,那么四边形![]() 的周长是( )
的周长是( ) A.5 B.10 C.15 D.209.如图,l1反映了某公司销售一种医疗器械的销售收入(万元)与销售量(台)之间的关系,l2反映了该公司销售该种医疗器械的销售成本(万元)与销售量(台)之间的关系.当销售收入大于销售成本时,该医疗器械才开始赢利.根据图象,则下列判断中错误的是( )
A.5 B.10 C.15 D.209.如图,l1反映了某公司销售一种医疗器械的销售收入(万元)与销售量(台)之间的关系,l2反映了该公司销售该种医疗器械的销售成本(万元)与销售量(台)之间的关系.当销售收入大于销售成本时,该医疗器械才开始赢利.根据图象,则下列判断中错误的是( )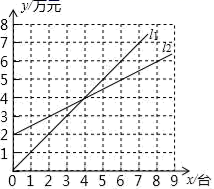 A.当销售量为4台时,该公司赢利4万元 B.当销售量多于4台时,该公司才开始赢利C.当销售量为2台时,该公司亏本1万元 D.当销售量为6台时,该公司赢利1万元10.下列根式中,与
A.当销售量为4台时,该公司赢利4万元 B.当销售量多于4台时,该公司才开始赢利C.当销售量为2台时,该公司亏本1万元 D.当销售量为6台时,该公司赢利1万元10.下列根式中,与![]() 不是同类二次根式的是( )A.
不是同类二次根式的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,菱形ABCD的对角线长分别为a、b,以菱形ABCD各边的中点为顶点作矩形
二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,菱形ABCD的对角线长分别为a、b,以菱形ABCD各边的中点为顶点作矩形![]() ,然后再以矩形
,然后再以矩形![]() 的中点为顶点作菱形
的中点为顶点作菱形![]() ,……,如此下去,得到四边形A2019B2019C2019D2019的面积用含a,b的代数式表示为___.
,……,如此下去,得到四边形A2019B2019C2019D2019的面积用含a,b的代数式表示为___.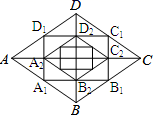 12.如果三角形三边长分别为
12.如果三角形三边长分别为![]() ,k,
,k,![]() ,则化简
,则化简![]() 得___________.13.在函数
得___________.13.在函数![]() 中,自变量
中,自变量![]() 的取值范围是________.14.已知:正方形ABCD的边长为8,点E、F分别在AD、CD上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为_____.
的取值范围是________.14.已知:正方形ABCD的边长为8,点E、F分别在AD、CD上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为_____.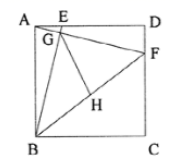 15.将直线
15.将直线![]() 沿y轴向上平移5个单位长度后,所得图象对应的函数关系式为_________.16.在一次“人与环境”知识竞赛中,共有25个题,每题四个答案,其中只有一个答案正确,每选对一题得4分,不选或选错倒扣2分,如果一个学生在本次竞赛中得分不低于60分,那么他至少要答对______题
沿y轴向上平移5个单位长度后,所得图象对应的函数关系式为_________.16.在一次“人与环境”知识竞赛中,共有25个题,每题四个答案,其中只有一个答案正确,每选对一题得4分,不选或选错倒扣2分,如果一个学生在本次竞赛中得分不低于60分,那么他至少要答对______题![]() 三、解下列各题(本大题共8小题,共72分)17.(8分)已知一次函数
三、解下列各题(本大题共8小题,共72分)17.(8分)已知一次函数![]() 与正比例函数
与正比例函数![]() 都经过点
都经过点![]() ,
,![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,且
,且![]() .(1)求
.(1)求![]() 与
与![]() 的解析式;(2)求⊿
的解析式;(2)求⊿![]() 的面积. 18.(8分)
的面积. 18.(8分)![]() 计算:
计算:![]() ;
;![]() 如图,已知直线
如图,已知直线![]() 的解析式为
的解析式为![]() ,直
,直![]() 的解析式为:
的解析式为:![]() ,
,![]() 与x轴交于点C,
与x轴交于点C,![]() 与x轴交于点B,
与x轴交于点B,![]() 与
与![]() 交于点
交于点![]() .
.![]() 求k,b的值;
求k,b的值;![]() 求三角形ABC的面积.
求三角形ABC的面积.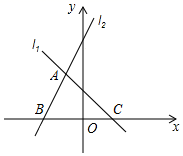 19.(8分)光明玩具商店用800元购进若干套悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用1500元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.(1)求第一批悠悠球每套的进价是多少元?(2)如果这两批悠悠球每套售价相同,且全部售完后总利润不低于20%,那么每套悠悠球的售价至少是多少元? 20.(8分)某中学数学活动小组为了调查居民的用水情况,从某社区的
19.(8分)光明玩具商店用800元购进若干套悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用1500元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.(1)求第一批悠悠球每套的进价是多少元?(2)如果这两批悠悠球每套售价相同,且全部售完后总利润不低于20%,那么每套悠悠球的售价至少是多少元? 20.(8分)某中学数学活动小组为了调查居民的用水情况,从某社区的![]() 户家庭中随机抽取了
户家庭中随机抽取了![]() 户家庭的月用水量,结果如下表所示:月用水量(吨)
户家庭的月用水量,结果如下表所示:月用水量(吨)![]()
![]()
![]()
![]()
![]()
![]()
![]() 户数
户数![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 求这
求这![]() 户家庭月用水量的平均数、众数和中位数;
户家庭月用水量的平均数、众数和中位数;![]() 根据上述数据,试估计该社区的月用水量;
根据上述数据,试估计该社区的月用水量;![]() 由于我国水资源缺乏,许多城市常利用分段计费的方法引导人们节约用水,即规定每个家庭的月基本用水量为
由于我国水资源缺乏,许多城市常利用分段计费的方法引导人们节约用水,即规定每个家庭的月基本用水量为![]() (吨),家庭月用水量不超过
(吨),家庭月用水量不超过![]() (吨)的部分按原价收费,超过
(吨)的部分按原价收费,超过![]() (吨)的部分加倍收费.你认为上述问题中的平均数、众数和中位数中哪一个量作为月基本用水量比较合适?简述理由. 21.(8分)如图,在平行四边形ABCD中,DB=DC,AE⊥BD于点E.若
(吨)的部分加倍收费.你认为上述问题中的平均数、众数和中位数中哪一个量作为月基本用水量比较合适?简述理由. 21.(8分)如图,在平行四边形ABCD中,DB=DC,AE⊥BD于点E.若![]() ,求
,求![]() 的度数.
的度数.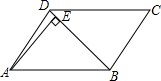 22.(10分)阳光小区附近有一块长100m,宽80m的长方形空地,在空地上有两条相同宽度的步道(一纵一横)和一个边长为步道宽度7倍的正方形休闲广场,两条步道的总面积与正方形休闲广场的面积相等,如图1所示.设步道的宽为a(m).
22.(10分)阳光小区附近有一块长100m,宽80m的长方形空地,在空地上有两条相同宽度的步道(一纵一横)和一个边长为步道宽度7倍的正方形休闲广场,两条步道的总面积与正方形休闲广场的面积相等,如图1所示.设步道的宽为a(m). 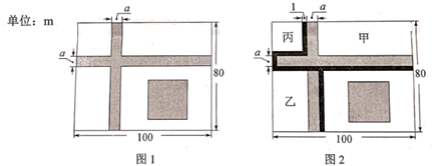 (1)求步道的宽.(2)为了方便市民进行跑步健身,现按如图2所示方案增建塑胶跑道.己知塑胶跑道的宽为1m,长方形区域甲的面积比长方形区域乙大441m2, 且区域丙为正方形,求塑胶跑道的总面积. 23.(10分)如图,在正方形ABCD中,E是AD的中点,F是 AB上一点,且AF=
(1)求步道的宽.(2)为了方便市民进行跑步健身,现按如图2所示方案增建塑胶跑道.己知塑胶跑道的宽为1m,长方形区域甲的面积比长方形区域乙大441m2, 且区域丙为正方形,求塑胶跑道的总面积. 23.(10分)如图,在正方形ABCD中,E是AD的中点,F是 AB上一点,且AF=![]() AB. 求证:CE⊥EF.
AB. 求证:CE⊥EF.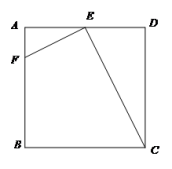 24.(12分)现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解甲、乙两家快递公司比较合适,甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.(1)当x>1时,请分別直接写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;(2)在(1)的条件下,小明选择哪家快递公司更省钱? 参考答案 一、选择题(每小题3分,共30分)1、B2、C3、A4、C5、A6、A7、A8、B9、A10、C 二、填空题(本大题共有6小题,每小题3分,共18分)11、
24.(12分)现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解甲、乙两家快递公司比较合适,甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.(1)当x>1时,请分別直接写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;(2)在(1)的条件下,小明选择哪家快递公司更省钱? 参考答案 一、选择题(每小题3分,共30分)1、B2、C3、A4、C5、A6、A7、A8、B9、A10、C 二、填空题(本大题共有6小题,每小题3分,共18分)11、![]() 12、11-3k.13、x≠114、515、
12、11-3k.13、x≠114、515、![]() 16、19 三、解下列各题(本大题共8小题,共72分)17、(1)
16、19 三、解下列各题(本大题共8小题,共72分)17、(1)![]() 或
或![]() ;⊿
;⊿![]() 的面积为15个平方单位. 18、(1)3;(2)
的面积为15个平方单位. 18、(1)3;(2)![]() ,
,![]() ;
;![]() 的面积
的面积![]() .19、(1)20;(2)27.1.20、
.19、(1)20;(2)27.1.20、![]() 7;
7;![]() (吨);
(吨);![]() 众数或中位数较合理,21、68°22、(1)3.1m (2)199m223、证明见解析24、 (1)y甲=15x+7,y乙=16x+3(2)当1<x<4时,选乙快递公司省钱;当x=4时,选甲、乙两家快递公司快递费一样多;当x>4时,选甲快递公司省钱
众数或中位数较合理,21、68°22、(1)3.1m (2)199m223、证明见解析24、 (1)y甲=15x+7,y乙=16x+3(2)当1<x<4时,选乙快递公司省钱;当x=4时,选甲、乙两家快递公司快递费一样多;当x>4时,选甲快递公司省钱
相关试卷
这是一份江西省育华学校2023-2024学年九年级数学第一学期期末达标检测模拟试题含答案,共7页。试卷主要包含了正六边形的边心距与半径之比为,下列标志中是中心对称图形的是等内容,欢迎下载使用。
这是一份2023-2024学年江西省育华学校八上数学期末预测试题含答案,共7页。试卷主要包含了答题时请按要求用笔,下列分式中,是最简分式的是等内容,欢迎下载使用。
这是一份江西省育华学校2023-2024学年数学八上期末综合测试模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,不等式1+x≥2﹣3x的解是,的值是等内容,欢迎下载使用。








