


西藏省重点中学2022-2023学年数学七下期末调研模拟试题含答案
展开西藏省重点中学2022-2023学年数学七下期末调研模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.△ABC中∠A、∠B、∠C的对边分别是a、b、c,下列命题中的假命题是( )
A.如果∠C﹣∠B=∠A,则△ABC是直角三角形
B.如果c2=b2﹣a2,则△ABC是直角三角形,且∠C=90°
C.如果(c+a)(c﹣a)=b2,则△ABC是直角三角形
D.如果∠A:∠B:∠C=5:2:3,则△ABC是直角三角形
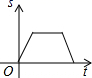
2.如图是小王早晨出门散步时,离家的距离s与时间t之间的函数图象.若用黑点表示小王家的位置,则小王散步行走的路线可能是( )
A.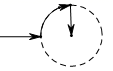 B.
B.![]() C.
C.![]() D.
D.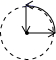
3.下列函数中,![]() 是
是![]() 的正比例函数的是( )
的正比例函数的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
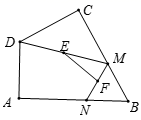
4.如图,在四边形![]() 中,
中,![]() ,点
,点![]() 分别为线段
分别为线段![]() 上的动点(含端点,但点
上的动点(含端点,但点![]() 不与点
不与点![]() 重合),点
重合),点![]() 分别为
分别为![]() 的中点,则
的中点,则![]() 长度的最大值为( )
长度的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.若式子![]() 在实数范围内有意义,则x的取值范围是( )
在实数范围内有意义,则x的取值范围是( )
A.x>![]() B.x>
B.x>![]() C.x≥
C.x≥![]() D.x≥
D.x≥![]()
6.在下列长度的各组线段中,能构成直角三角形的是( )
A.3,5,9 B.4,6,8 C.13,14,15 D.8,15,17
7.如图,△ABC中,∠C=90°,E、F分别是AC、BC上两点,AE=8,BF=6,点P、Q、D分别是AF、BE、AB的中点,则PQ的长为( )
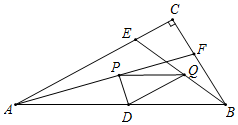
A.4 B.5 C.6 D.8
8.平移直线![]() 得到直线
得到直线![]() ,正确的平移方式是( )
,正确的平移方式是( )
A.向上平移![]() 个单位长度 B.向下平移
个单位长度 B.向下平移![]() 个单位长度
个单位长度
C.向左平移![]() 个单位长度 D.向右平移
个单位长度 D.向右平移![]() 个单位长度
个单位长度
9.下列代数式中,属于最简二次根式的是( )
A.![]() B.
B.![]() C.
C.![]()
![]() D.
D.![]()
10.调查50名学生的年龄,列频数分布表时,这些学生的年龄落在5个小组中,第一、二、三、五组数据个数分别是2,8,15,5,则第四组的频数是( )
A.20 B.30 C.0.4 D.0.6
11.为鼓励业主珍惜每一滴水,某小区物业表扬了100个节约用水模范户,5月份节约用水的情况如下表:那么,5月份这100户平均节约用水的吨数为( )吨.
每户节水量(单位:吨) | 1 | 1.2 | 1.5 |
节水户数 | 65 | 15 | 20 |
A.1 B.1.1 C.1.13 D.1.2
12.如图,将正方形网格放置在平面直角坐标系中,其中每个小正方形的边长均为1,![]() 经过平移后得到
经过平移后得到![]() ,若
,若![]() 上一点
上一点![]() 平移后对应点为
平移后对应点为![]() ,点
,点![]() 绕原点顺时针旋转
绕原点顺时针旋转![]() ,对应点为
,对应点为![]() ,则点
,则点![]() 的坐标为( )
的坐标为( )
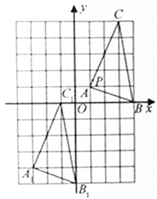
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每题4分,满分20分,将答案填在答题纸上)
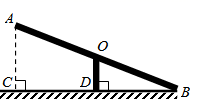
13.如图,跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=0.8m;当它的一端B地时,另一端A离地面的高度AC为____m.
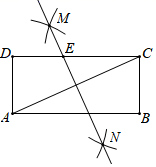
14.如图,在矩形ABCD中,按以下步骤作图:①分别以点A和点C为圆心,以大于![]() AC的长为半径作弧,两弧相交于点M和N;②作直线MN交CD于点E,若AB=8,AD=6,则EC=_____________.
AC的长为半径作弧,两弧相交于点M和N;②作直线MN交CD于点E,若AB=8,AD=6,则EC=_____________.
15.计算:![]() =______.
=______.
16.用配方法解一元二次方程x2-mx=1时,可将原方程配方成(x-3)2=n,则m+n的值是 ________ .
17.袋中装有除颜色外其余均相同的5个红球和3个白球.从袋中任意摸出一个球,则摸出的球是红球的概率为________.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)如图①,四边形![]() 是正方形,点
是正方形,点![]() 是边
是边![]() 的中点,
的中点,![]() ,且
,且![]() 交正方形的外角平分线
交正方形的外角平分线![]() 于点
于点![]() 请你认真阅读下面关于这个图形的探究片段,完成所提出的问题.
请你认真阅读下面关于这个图形的探究片段,完成所提出的问题.
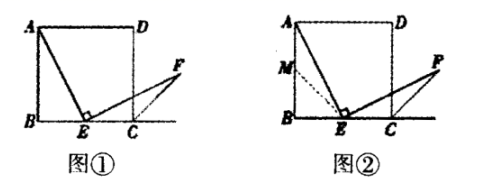
(1)探究1:小强看到图①后,很快发现![]() 这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(个直角三角形,一个钝角三角形)考虑到点E是边BC的中点,因此可以选取AB的中点M(如图②),连接EM后尝试着去证明
这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(个直角三角形,一个钝角三角形)考虑到点E是边BC的中点,因此可以选取AB的中点M(如图②),连接EM后尝试着去证明![]() 就行了.随即小强写出了如下的证明过程:
就行了.随即小强写出了如下的证明过程:
证明:如图②,取AB的中点M,连接EM.
∵![]()
∴![]()
又∵![]()
∴![]()
∵点E、M分别为正方形的边BC和AB的中点,
∴![]()
∴![]() 是等腰直角三角形,
是等腰直角三角形,![]()
∴![]()
又∵![]() 是正方形外角的平分线,
是正方形外角的平分线,
∴![]() ,∴
,∴![]()
∴![]()
∴![]() ,
,
∴![]()
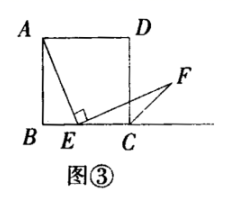
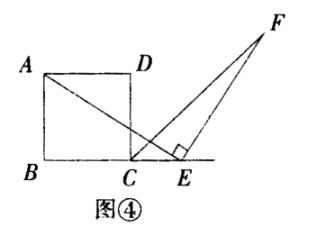
(2)探究2:小强继续探索,如图③,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,发现AE=EF仍然成立小强进一步还想试试,如图④,若把条件“点E是边BC的中点”为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF仍然成立请你选择图③或图④中的一种情况写出证明过程给小强看.
19.(5分)(1)化简;(m+2+![]() )•
)•![]()
(2)先化简,再求值;(![]() +x+2)÷
+x+2)÷![]() ,其中|x|=2
,其中|x|=2
20.(8分)甲、乙两台包装机同时包装![]() 的糖果,从中各抽出
的糖果,从中各抽出![]() 袋,测得实际质量(g)如下:甲:
袋,测得实际质量(g)如下:甲:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ;乙:
;乙:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
(1)分别计算两组数据的平均数(结果四舍五入保留整数)和方差;
(2)哪台包装机包装糖果的质量比较稳定(方差公式:![]() )
)
21.(10分)如图,已知直线l1:y=-2x+4与x、y轴分别交于点N、C,与直线l2:y=kx+b(k≠0)交于点M,点M的横坐标为1,直线l2与x轴的交点为A(-2,0)
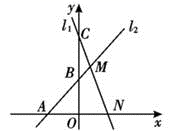
(1)求k,b的值;
(2)求四边形MNOB的面积.
22.(10分)如图,![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 移动,同时,点
移动,同时,点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 的延长线移动,已知点
的延长线移动,已知点![]() 、
、![]() 的移动速度相同,
的移动速度相同,![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
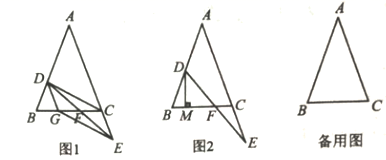
(1)如图1,当点![]() 在线段
在线段![]() 上时,过点
上时,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,求证:点
,求证:点![]() 是
是![]() 的中点;
的中点;
(2)如图2,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,当点
,当点![]() 、
、![]() 在移动过程中,线段
在移动过程中,线段![]() 、
、![]() 、
、![]() 有何数量关系?请直接写出你的结论: .
有何数量关系?请直接写出你的结论: .
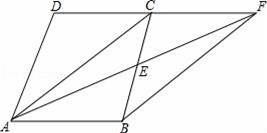
23.(12分)已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、B
2、D
3、A
4、B
5、D
6、D
7、B
8、A
9、A
10、A
11、C
12、A
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、1.6
14、![]()
15、![]() .
.
16、16
17、![]()
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、见解析
19、(1)m+1;(2)1
20、(1)![]() ,
,![]()
![]() ,
,![]() ,
,![]() ;(2)乙包装机包装的质量比较稳定.
;(2)乙包装机包装的质量比较稳定.
21、(1)k= ![]() ,b=
,b= ![]() ;(2)
;(2)![]()
22、(1)见解析;(2)![]() 或
或![]() .
.
23、四边形ABFC是平行四边形;证明见解析.
资阳市重点中学2022-2023学年七下数学期末调研试题含答案: 这是一份资阳市重点中学2022-2023学年七下数学期末调研试题含答案,共6页。
崇左市重点中学2022-2023学年数学七下期末调研试题含答案: 这是一份崇左市重点中学2022-2023学年数学七下期末调研试题含答案,共7页。试卷主要包含了分式有意义,x的取值范围是,下列说法,如图,△ABC顶点C的坐标是等内容,欢迎下载使用。
宝鸡市重点中学2022-2023学年数学七下期末调研模拟试题含答案: 这是一份宝鸡市重点中学2022-2023学年数学七下期末调研模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,当压力F等内容,欢迎下载使用。












