2024版新教材高考数学全程一轮总复习第八章解析几何第四节直线与圆圆与圆的位置关系课件

这是一份2024版新教材高考数学全程一轮总复习第八章解析几何第四节直线与圆圆与圆的位置关系课件，共53页。PPT课件主要包含了必备知识·夯实双基，关键能力·题型突破，dr1＋r2，dr1－r2，d＝r1－r2，d＝r1＋r2，答案B，答案C，题后师说，答案D等内容，欢迎下载使用。
【课标标准】　1.能根据给定直线、圆的方程，判断直线与圆、圆与圆的位置关系.2.能用直线和圆的方程解决一些简单的数学问题与实际问题．
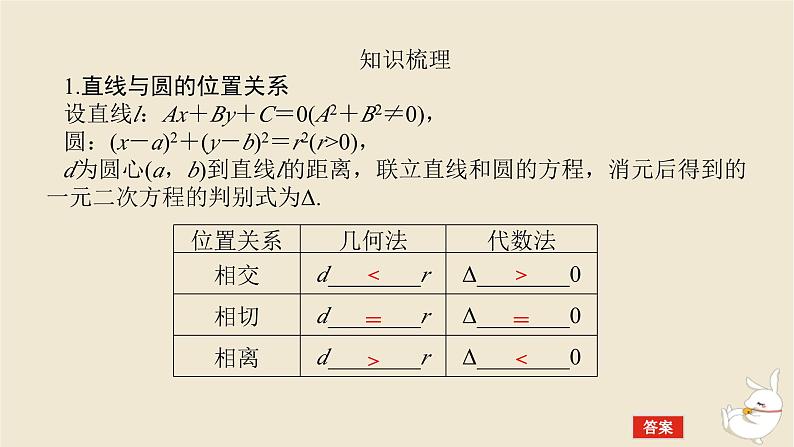
知识梳理1.直线与圆的位置关系设直线l：Ax＋By＋C＝0(A2＋B2≠0)，圆：(x－a)2＋(y－b)2＝r2(r>0)，d为圆心(a，b)到直线l的距离，联立直线和圆的方程，消元后得到的一元二次方程的判别式为Δ.
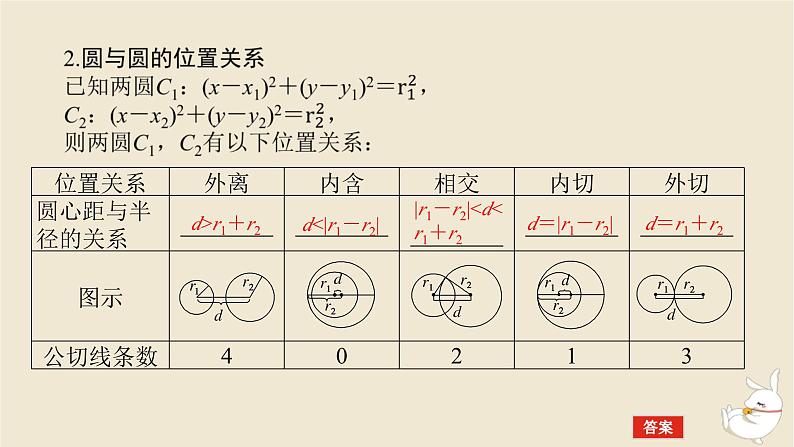
|r1－r2|0)所得弦长之比为3∶1，则r＝_______．
角度三 切线问题例3 (1)直线mx＋(m＋1)y－2＝0(m∈R)与圆(x－1)2＋(y－1)2＝1相切，则m＝(　　)A．1 B．3C．0或1 D．0或3
(2)[2023·河南南阳模拟]若圆C：(x＋1)2＋(y－2)2＝2关于直线2ax＋by＋6＝0对称，由点P(a，b)向圆C作切线，切点为A，则|PA|的最小值是(　　)A．6　 　B．4 C．3　 　D．2
题后师说 解决直线与圆相切问题的策略
巩固训练3(1)[2023·广东广州期末]过点(2，2)作圆(x－1)2＋y2＝5的切线，则切线方程为(　　)A．x－2y＋2＝0B．3x＋2y－10＝0C．x＋2y－6＝0D．x＝2或x＋2y－6＝0
(2)点P在圆C：(x－3)2＋(y－3)2＝4上，A(2，0)，B(0，1)，则∠PBA最大时，|PB|＝______．
题型二　圆与圆的位置关系例4 (1)[2023·安徽十校联考]已知直线l：mx＋y－3m－2＝0与圆M：(x－5)2＋(y－4)2＝25交于A，B两点，则当弦AB最短时，圆M与圆N：(x＋2m)2＋y2＝9的位置关系是(　　)A．内切　　B．外离　　C．外切　　D．相交
题后师说(1)处理与两圆的位置关系相关的问题时，多用圆心距与两圆半径的和或差的大小关系判断，一般不采用代数法．(2)若两圆相交，则两圆公共弦所在直线的方程可由两圆的方程作差得到．(3)求两圆公共弦长时，在其中一圆中，弦心距、半弦长、半径构成直角三角形，利用勾股定理求解．
3．[2021·新高考Ⅱ卷]已知直线l：ax＋by－r2＝0(r>0)与圆C：x2＋y2＝r2，点A(a，b)，则下列说法正确的是(　　)A．若点A在圆C上，则直线l与圆C相切B．若点A在圆C内，则直线l与圆C相离C．若点A在圆C外，则直线l与圆C相离D．若点A在直线l上，则直线l与圆C相切
4．[2022·新高考Ⅰ卷]写出与圆x2＋y2＝1和(x－3)2＋(y－4)2＝16都相切的一条直线的方程________________．
解析：由题意知两圆的圆心和半径分别为O1(0，0)，O2(3，4)，r1＝1，r2＝4.因为|O1O2|＝r1＋r2，所以两圆外切．由两圆外切，画出示意图，如图．
5．[2022·新高考Ⅱ卷]设点A(－2，3)，B(0，a)，若直线AB关于y＝a对称的直线与圆(x＋3)2＋(y＋2)2＝1有公共点，则a的取值范围是________.
6．[2022·全国乙卷]过四点(0，0)，(4，0)，(－1，1)，(4，2)中的三点的一个圆的方程为__________________．
(x－2)2＋(y－3)2＝13