


2024版新教材高考数学全程一轮总复习第二章函数与基本初等函数第二节函数的单调性和最值课件
展开【课标标准】 借助函数图象,会用符号语言表达函数的单调性、最大值、最小值,理解它们的作用和实际意义.
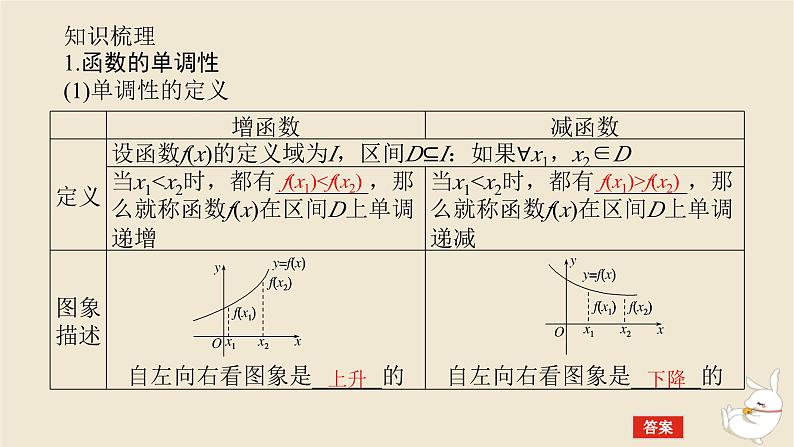
知识梳理1.函数的单调性(1)单调性的定义
f(x1)
(2)单调区间的定义如果函数y=f(x)在区间D上________或________,则称函数y=f(x)在这一区间上具有(严格的)单调性,区间D叫做y=f(x)的单调区间.
5.(易错)若函数f(x)=x2+2(a-1)x+2的单调递减区间是(-∞,4],则实数a的值是________.
解析:因为函数f(x)的单调递减区间是(-∞,4],且函数f(x)的图象对称轴为直线x=1-a,所以有1-a=4,即a=-3.
(3)[2023·江苏南通月考]设函数f(x)=-x2+2x+8,g(x)=lgax(0
巩固训练1(1)函数f(x)=ln (x2-2x-8)的单调递增区间是( )A.(-∞,-2) B.(-∞,1)C.(1,+∞) D.(4,+∞)
解析:由x2-2x-8>0,得f(x)的定义域为{x|x>4或x<-2}.设t=x2-2x-8,则y=ln t为增函数.要求函数f(x)的单调递增区间,即求函数t=x2-2x-8的单调递增区间(定义域内).∵函数t=x2-2x-8在(4,+∞)上单调递增,在(-∞,-2)上单调递减,∴函数f(x)的单调递增区间为(4,+∞).故选D.
题后师说1.判断函数单调性的方法(1)图象法 (2)利用已知函数的单调性 (3)定义法2.证明函数单调性的方法(1)定义法(2)导数法
题后师说比较函数值的大小时,若自变量的值不在同一个单调区间内,要利用函数的性质,转化到同一个单调区间内进行比较.
题后师说利用函数单调性求最值是求函数最值的重要方法,特别是当函数图象不易作出时,单调性法几乎成为首选方法.
题后师说在求解与抽象函数有关的不等式时,往往是利用函数的单调性将“f”符号脱掉,使其转化为具体的不等式求解.此时,应特别注意函数的定义域.
巩固训练5已知函数y=f(x)在定义域(-1,1)上是减函数,且f(1-a)
高中数学高考2018高考数学(理)大一轮复习课件:第二章 函数的概念与基本初等函数Ⅰ 第二节 函数的单调性与最值: 这是一份高中数学高考2018高考数学(理)大一轮复习课件:第二章 函数的概念与基本初等函数Ⅰ 第二节 函数的单调性与最值,共40页。
高考数学一轮复习配套课件 第二章 第二节 函数的单调性与最值: 这是一份高考数学一轮复习配套课件 第二章 第二节 函数的单调性与最值,共57页。PPT课件主要包含了必备知识基础落实,关键能力考点突破,微专题,增函数,减函数,上升的,下降的,单调区间,f′x0,fx≤M等内容,欢迎下载使用。
高考数学(理数)一轮复习课件:第二章 函数的概念与基本初等函数Ⅰ 第二节 函数的单调性与最值 (含详解): 这是一份高考数学(理数)一轮复习课件:第二章 函数的概念与基本初等函数Ⅰ 第二节 函数的单调性与最值 (含详解),共40页。