2024版新教材高考数学全程一轮总复习第二章函数与基本初等函数第四节二次函数与幂函数课件

这是一份2024版新教材高考数学全程一轮总复习第二章函数与基本初等函数第四节二次函数与幂函数课件，共38页。PPT课件主要包含了必备知识·夯实双基，关键能力·题型突破，b＝0，y＝xα，单调递增，单调递减，答案D，答案A，答案C，－∞1等内容，欢迎下载使用。

知识梳理1.二次函数(1)二次函数解析式的三种形式一般式：f(x)＝______________．顶点式：f(x)＝a(x－m)2＋n(a≠0)，顶点坐标为________．两根式：f(x)＝a(x－x1)(x－x2)(a≠0)，x1，x2为f(x)的________．
ax2＋bx＋c(a≠0)
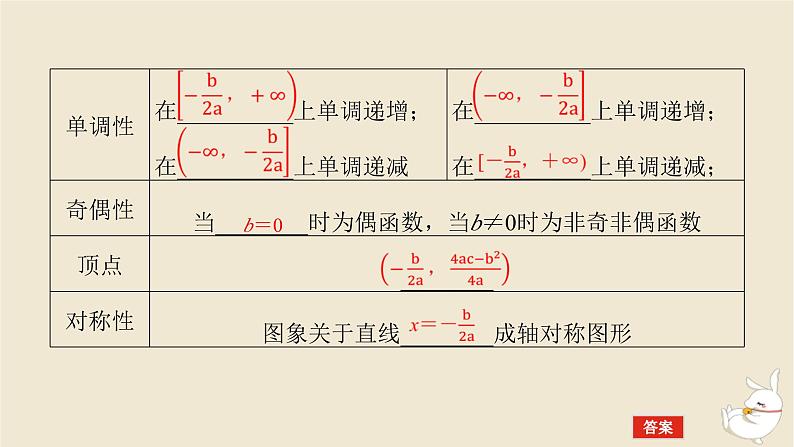
(2)二次函数的图象与性质
2.幂函数(1)幂函数的概念一般地，函数________叫做幂函数，其中x是自变量，α是常数．(2)常见的五种幂函数的图象
(3)幂函数的性质①幂函数在(0，＋∞)上都有定义．②当α>0时，幂函数的图象都过点(1，1)和(0，0)，且在(0，＋∞)上________．③当α<0时，幂函数的图象都过点(1，1)，且在(0，＋∞)上________．
2．(教材改编)已知某二次函数的图象与函数y＝2x2的图象的形状一样，开口方向相反，且其顶点为(－1，3)，则此函数的解析式为(　　)A．y＝2(x－1)2＋3　 　B．y＝2(x＋1)2＋3C．y＝－2(x－1)2＋3 D．y＝－2(x＋1)2＋3
解析：设所求函数的解析式为y＝－2(x＋h)2＋k(a≠0)，根据顶点为(－1，3)，可得h＝1，且k＝3，故所求的函数解析式为y＝－2(x＋1)2＋3.故选D.
解析：因为幂函数f(x)＝xα为奇函数，所以α可取－1，1，3，又f(x)＝xα在(0，＋∞)上递减，所以α＜0，故α＝－1.
5．(易错)如果函数f(x)＝ax2＋2x－3在区间(－∞，4)上单调递增，则实数a的取值范围是________．
(3)[2023·河南商丘模拟]已知幂函数f(x)的图象过点(－8，－2)，且f(a＋1)≤－f(a－3)，则a的取值范围是________.
题后师说幂函数图象与性质问题的求解策略
解析：根据函数图象可得：①对应的幂函数y＝xα在[0，＋∞)上单调递增，且增长速度越来越慢，故α∈(0，1)，故D选项符合要求．故选D.
题型二　二次函数的解析式例 2 已知二次函数f(x)满足f(2)＝－1，f(－1)＝－1，且f(x)的最大值是8，试确定此二次函数的解析式． 
题后师说求二次函数解析式的策略
巩固训练2已知二次函数f(x)与x轴的两个交点坐标分别为(0，0)和(－2，0)，且有最小值－1，求f(x)的解析式．
题型三　二次函数的图象与性质角度一 二次函数的图象例 3 [2023·广东茂名模拟](多选)二次函数y＝ax2＋bx＋c的图象如图所示，则下列说法正确的是(　　)A．2a＋b＝0 B．4a＋2b＋c<0C．9a＋3b＋c<0 D．abc<0
题后师说识别二次函数图象应学会“三看”
巩固训练3已知函数y＝ax2＋bx＋c，如果a>b>c且a＋b＋c＝0，则它的图象可能是(　　)
解析：由题意，函数y＝ax2＋bx＋c，因为a＋b＋c＝0，令x＝1，可得y＝a＋b＋c＝0，即函数图象过点(1，0)，又由a>b>c，可得a>0，c<0，所以抛物线的开口向上，可排除B、D项；令x＝0，可得y＝c<0，可排除C项；故选A.
角度二 二次函数的最值例 4 已知关于x的函数y＝x2－2mx＋4.(1)当x∈[－2，3]时，求函数y＝x2－2mx＋4的最大值；(2)当x∈[－2，3]时，若函数最小值为2，求m的值．
题后师说求二次函数在闭区间上最值的类型及策略
巩固训练4函数f(x)＝x2－2x－2.(1)当x∈[－2，2]时，求函数f(x)的最值；(2)当x∈[t，t＋1]时，求函数f(x)的最小值．