2024版新教材高考数学全程一轮总复习第十章计数原理概率随机变量及其分布第五节离散型随机变量的分布列均值与方差课件

这是一份2024版新教材高考数学全程一轮总复习第十章计数原理概率随机变量及其分布第五节离散型随机变量的分布列均值与方差课件，共51页。PPT课件主要包含了必备知识·夯实双基，关键能力·题型突破，aEX＋b，a2DX，答案A，答案C，答案D，答案AC等内容，欢迎下载使用。

【课标标准】　1.了解离散型随机变量的概念.2.理解离散型随机变量分布列及其数字特征(均值、方差)． 
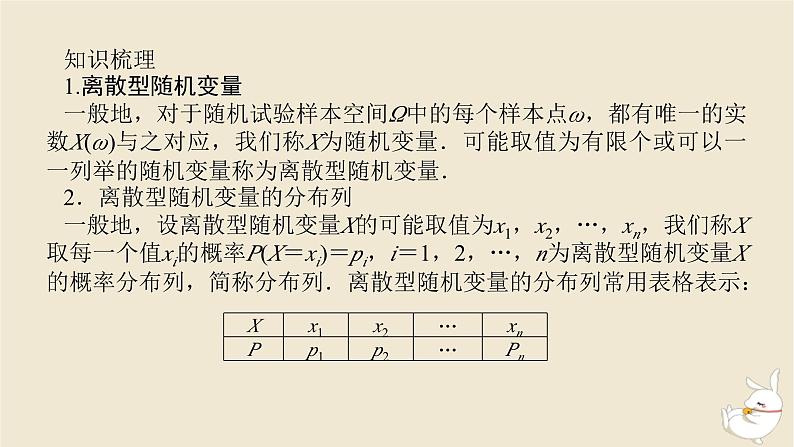
知识梳理1.离散型随机变量一般地，对于随机试验样本空间Ω中的每个样本点ω，都有唯一的实数X(ω)与之对应，我们称X为随机变量．可能取值为有限个或可以一一列举的随机变量称为离散型随机变量．2．离散型随机变量的分布列一般地，设离散型随机变量X的可能取值为x1，x2，…，xn，我们称X取每一个值xi的概率P(X＝xi)＝pi，i＝1，2，…，n为离散型随机变量X的概率分布列，简称分布列．离散型随机变量的分布列常用表格表示：
3.离散型随机变量的分布列的性质(1)pi________0，i＝1，2，…，n.(2)p1＋p2＋…＋pn＝________．
4．离散型随机变量的均值与方差一般地，若离散型随机变量X的分布列为(1)均值称E(X)＝________________＝________为随机变量X的均值或数学期望，数学期望简称期望．
x1p1＋x2p2＋…＋xnpn
[常用结论]均值与方差的四个常用性质(1)E(k)＝k，D(k)＝0，其中k为常数．(2)E(X1＋X2)＝E(X1)＋E(X2)．(3)D(X)＝E(X2)－(E(X))2.(4)若X1，X2相互独立，则E(X1X2)＝E(X1)·E(X2)． 
夯实双基1.思考辨析(正确的打“√”，错误的打“×”)(1)测量全校所有同学的身高，在170 cm～175 cm之间的人数是离散型随机变量．(　　)(2)离散型随机变量的各个可能值表示的事件是彼此互斥的．(　　)(3)离散型随机变量分布列中，随机变量取各个值的概率之和可以小于1.(　　)(4)随机变量的方差和标准差都反映了随机变量取值偏离均值的平均程度，方差或标准差越小，则偏离均值的平均程度越小．(　　)
3．(教材改编)甲、乙两工人在一天生产中出现的废品数分别是两个随机变量X，Y，其分布列分别为若甲、乙两人的日产量相等，则甲、乙两人中技术较好的是________．
解析：根据出现废品数分别是两个随机变量X、Y的分布列，得到甲生产废品期望是1×0.3＋2×0.2＋3×0.1＝1，乙生产废品期望是1×0.5＋2×0.2＝0.9，∵甲生产废品期望大于乙生产废品期望，∴甲、乙两人中技术较好的是乙．
4．(易错)袋中有3个白球，5个黑球，从中任取2个，可以作为随机变量的是(　　)A．至少取到1个白球 B．至多取到1个白球C．取到白球的个数 D．取到的球的个数
解析：选项A，B是随机事件； 选项D是定值2；选项C可能的取值为0，1，2，可以用随机变量表示．
5．(易错)已知离散型随机变量X的分布列为：则常数q＝________．
题后师说离散型随机变量的分布列性质的应用
题后师说离散型随机变量分布列的求解步骤
巩固训练24月23日是“世界读书日”，学校开展了一系列的读书教育活动．学校为了解高二学生课外阅读情况，从高二某班甲、乙、丙、丁四个读书小组(每名学生只能参加一个读书小组)学生中抽取12名学生参加问卷调查．各组人数统计如下：(1)从参加问卷调查的12名学生中随机抽取2人，求这2人来自同一个小组的概率；(2)从已抽取的甲、丙两个小组的学生中随机抽取2个，用X表示抽得甲组学生的人数，求随机变量X的分布列． 
题型三　离散型随机变量的均值与方差角度一 均值与方差的计算例 3 (1)[2023·山东菏泽期末](多选)设离散型随机变量X的分布列为：若离散型随机变量Y满足：Y＝2X＋1，则下列结论正确的有(　　)A．E(X)＝2 B．E(Y)＝4C．D(X)＝1.8 D．D(Y)＝3.6
解析：由分布列知：q＝0.1，E(X)＝0×0.1＋1×0.4＋2×0.1＋3×0.2＋4×0.2＝2，A正确；E(Y)＝E(2X＋1)＝2E(X)＋1＝5，B不正确；对于C，D(X)＝0.1×22＋0.4×12＋0.1×02＋0.2×12＋0.2×22＝1.8，正确；对于D，D(Y)＝D(2X＋1)＝4D(X)＝7.2，不正确．故选AC.
(2)某网约车司机统计了自己一天中出车一次的总路程X(单位：km)的可能取值是20，22，24，26，28，30，它们出现的概率依次是0.1，0.2，0.3，0.1，t，2t.①求X的分布列，并求X的均值和方差；②若网约车计费细则如下：起步价为5元，行驶路程不超过3 km时，收费5元，行驶路程超过3 km时，则按每超出1 km(不足1 km也按1 km计程)收费3元计费．试计算此人一天中出车一次收入的均值和方差．
解析：①由题意，得0.1＋0.2＋0.3＋0.1＋t＋2t＝1.∴t＝0.1.∴X的分布列为∴E(X)＝20×0.1＋22×0.2＋24×0.3＋26×0.1＋28×0.1＋30×0.2＝25，D(X)＝(－5)2×0.1＋(－3)2×0.2＋(－1)2×0.3＋12×0.1＋32×0.1＋52×0.2＝10.6.②设此人一天中出车一次的收入为Y元，则Y＝3(X－3)＋5＝3X－4(X>3，X∈N)，∴E(Y)＝E(3X－4)＝3E(X)－4＝3×25－4＝71，D(Y)＝D(3X－4)＝32·D(X)＝95.4.故此人一天中出车一次收入的均值为71元，方差为95.4.
题后师说1.求离散型随机变量的均值与方差关键是确定随机变量的所有可能值，写出随机变量的分布列，正确运用均值、方差公式进行计算．2．注意E(aX＋b)＝aE(X)＋b，D(aX＋b)＝a2D(X)的应用．
角度二 决策问题例 4 [2023·河北保定期末]某车间打算购买2台设备，该设备有一个易损零件，在购买设备时可以额外购买这种易损零件作为备件，价格为每个100元．在设备使用期间，零件损坏，备件不足再临时购买该零件，价格为每个300元．在使用期间，每台设备需要更换的零件个数m的分布列为X表示2台设备使用期间需更换的零件数，n代表购买2台设备的同时购买易损零件的个数．(1)求X的分布列；(2)以购买易损零件所需费用的期望为决策依据，试问在n＝11和n＝12中，应选哪一个？
解析：(1)X的可能取值为10，11，12，13，14，P(X＝10)＝0.3×0.3＝0.09，P(X＝11)＝2×0.3×0.5＝0.3，P(X＝12)＝2×0.3×0.2＋0.5×0.5＝0.37，P(X＝13)＝2×0.5×0.2＝0.2，P(X＝14)＝0.2×0.2＝0.04，则X的分布列为：
(2)记Y1为当n＝11时购买零件所需费用，P(Y1＝1 100元)＝P(X≤11)＝0.39，P(Y1＝1 400元)＝P(X＝12)＝0.37，P(Y1＝1 700元)＝P(X＝13)＝0.2，P(Y1＝2 000元)＝P(X＝14)＝0.04，E(Y1)＝1 100×0.39＋1 400×0.37＋1 700×0.2＋2 000×0.04＝1 367(元)，记Y2为当n＝12时购买零件所需费用，P(Y2＝1 200元)＝P(X≤12)＝0.76，P(Y2＝1 500元)＝P(X＝13)＝0.2，P(Y2＝1 800元)＝P(X＝14)＝0.04，E(Y2)＝1 200×0.76＋1 500×0.2＋1 800×0.04＝1 284(元)，显然E(Y1)>E(Y2)，所以应选择n＝12.
题后师说随机变量的均值和方差从整体和全局上刻画了随机变量，是生产实际中用于方案取舍的重要依据．一般先比较均值，若均值相同，再用方差决定．
1.[2022·全国甲卷]甲、乙两个学校进行体育比赛，比赛共设三个项目，每个项目胜方得10分，负方得0分，没有平局．三个项目比赛结束后，总得分高的学校获得冠军．已知甲学校在三个项目中获胜的概率分别为0.5，0.4，0.8，各项目的比赛结果相互独立．(1)求甲学校获得冠军的概率；(2)用X表示乙学校的总得分，求X的分布列与期望．
(2)由题意得，X的所有可能取值为0，10，20，30.易知乙学校在三个项目中获胜的概率分别为0.5，0.6，0.2，则P(X＝0)＝(1－0.5)×(1－0.6)×(1－0.2)＝0.16，P(X＝10)＝0.5×(1－0.6)×(1－0.2)＋(1－0.5)×0.6×(1－0.2)＋(1－0.5)×(1－0.6)×0.2＝0.44，P(X＝20)＝0.5×0.6×(1－0.2)＋0.5×(1－0.6)×0.2＋(1－0.5)×0.6×0.2＝0.34，P(X＝30)＝0.5×0.6×0.2＝0.06，所以X的分布列为则E(X)＝0×0.16＋10×0.44＋20×0.34＋30×0.06＝13.
2．[2022·北京卷]在校运动会上，只有甲、乙、丙三名同学参加铅球比赛，比赛成绩达到9.50 m以上(含9.50 m)的同学将获得优秀奖．为预测获得优秀奖的人数及冠军得主，收集了甲、乙、丙以往的比赛成绩，并整理得到如下数据(单位：m)：甲：9.80，9.70，9.55，9.54，9.48，9.42，9.40，9.35，9.30，9.25；乙：9.78，9.56，9.51，9.36，9.32，9.23；丙：9.85，9.65，9.20，9.16.假设用频率估计概率，且甲、乙、丙的比赛成绩相互独立(1)估计甲在校运动会铅球比赛中获得优秀奖的概率；(2)设X是甲、乙、丙在校运动会铅球比赛中获得优秀奖的总人数，估计X的数学期望EX；(3)在校运动会铅球比赛中，甲、乙、丙谁获得冠军的概率估计值最大？(结论不要求证明) 
(3)丙．理由如下：由题意可得，甲、乙、丙三人参赛的结果共有10×6×4＝240(种)．丙获得冠军的结果有10×6＋8×5＝100(种)，乙获得冠军的结果有9×3＋8×2＋6×2＋3×2＋2×2＝65(种)，甲获得冠军的结果有240－100－65＝75(种)，所以丙获得冠军的概率估计值最大．
3．[2021·新高考Ⅰ卷]某学校组织“一带一路”知识竞赛，有A，B两类问题．每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答，若回答错误则该同学比赛结束；若回答正确则从另一类问题中再随机抽取一个问题回答，无论回答正确与否，该同学比赛结束．A类问题中的每个问题回答正确得20分，否则得0分；B类问题中的每个问题回答正确得80分，否则得0分，已知小明能正确回答A类问题的概率为0.8，能正确回答B类问题的概率为0.6，且能正确回答问题的概率与回答次序无关．(1)若小明先回答A类问题，记X为小明的累计得分，求X的分布列；(2)为使累计得分的期望最大，小明应选择先回答哪类问题？并说明理由． 
解析：(1)由题可知，X的所有可能取值为0，20，100.P(X＝0)＝1－0.8＝0.2；P(X＝20)＝0.8(1－0.6)＝0.32；P(X＝100)＝0.8×0.6＝0.48.所以X的分布列为