初中数学27.2.1 相似三角形的判定教学ppt课件

这是一份初中数学27.2.1 相似三角形的判定教学ppt课件，共16页。PPT课件主要包含了学习重难点，复习导入，方法2通过平行线，例题讲解，当堂训练，△ABC∽△ADE等内容，欢迎下载使用。
1、掌握判定两个三角形相似的两种方法：三边法，两边及夹角法。2、会用本节课学习的三边法，两边及夹角法来证明有关问题。3、通过用三角形全等的判定方法类比得出三角形相似的判定方法，初步领悟类比的思想方法。4、经历从实验探究到归纳证明的过程，发展合情推理能力。
重点：三边法，两边及夹角法及其应用
难点：探究三边法，两边及夹角法的推理过程
问题1：两个三角形全等有哪些判定方法？
SSS,SAS,ASA,AAS,
对于Rt △,还可以用HL
问题2：我们学过哪些判定三角形相似的方法？
问题3：全等三角形与相似三角形有怎样的关系？
方法1：通过定义（不常用）
∵ DE∥BC∴△ADE∽△ABC
全等三角形是特殊的相似三角形
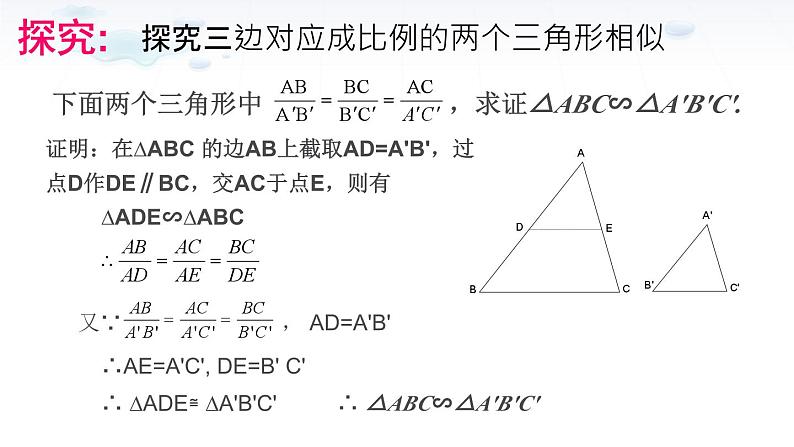
探究三边对应成比例的两个三角形相似
下面两个三角形中 ，求证△ABC∽△A′B′C′.
证明：在∆ABC 的边AB上截取AD=A'B'，过点D作DE∥BC，交AC于点E，则有
又∵ ， AD=A'B'
∴AE=A'C', DE=B' C'
∴ ∆ADE≌ ∆A'B'C'
∴ △ABC∽△A′B′C′
△ABC∽△A′B′C′
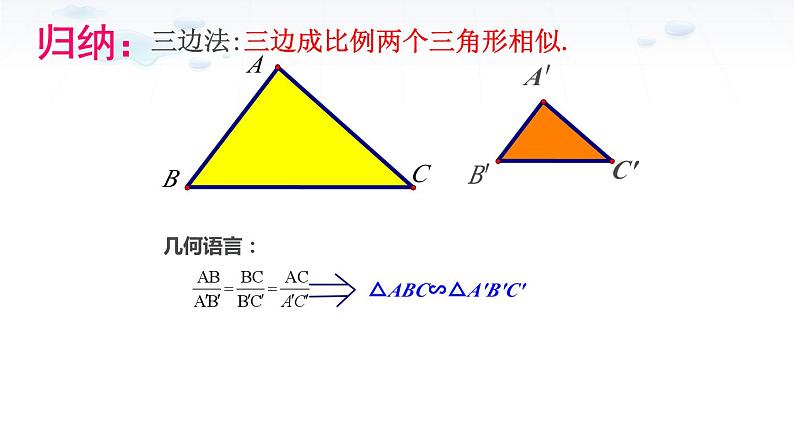
三边法:三边成比例两个三角形相似.
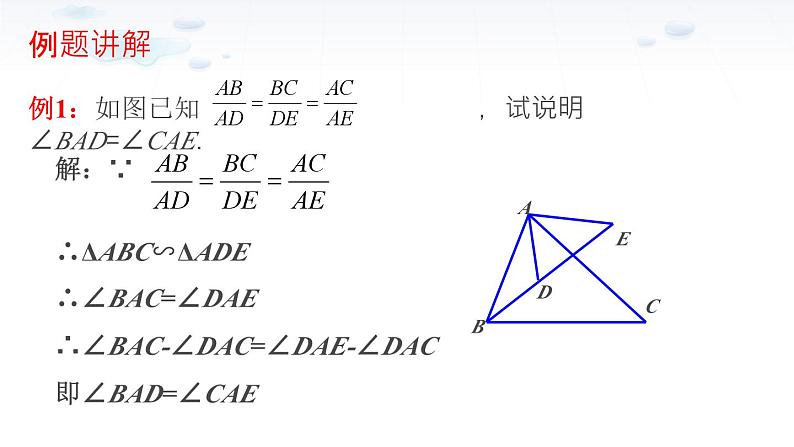
例1：如图已知 ，试说明∠BAD=∠CAE.
解：∵ ∴ΔABC∽ΔADE∴∠BAC=∠DAE∴∠BAC-∠DAC=∠DAE-∠DAC即∠BAD=∠CAE
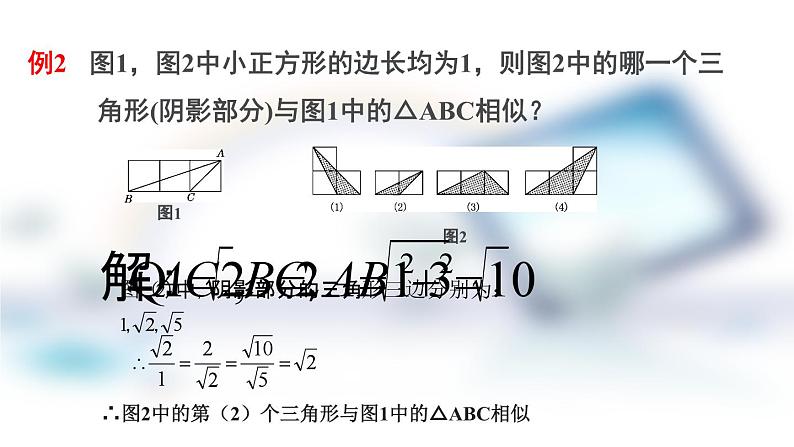
例2 图1，图2中小正方形的边长均为1，则图2中的哪一个三角形(阴影部分)与图1中的△ABC相似？
∴图2中的第（2）个三角形与图1中的△ABC相似
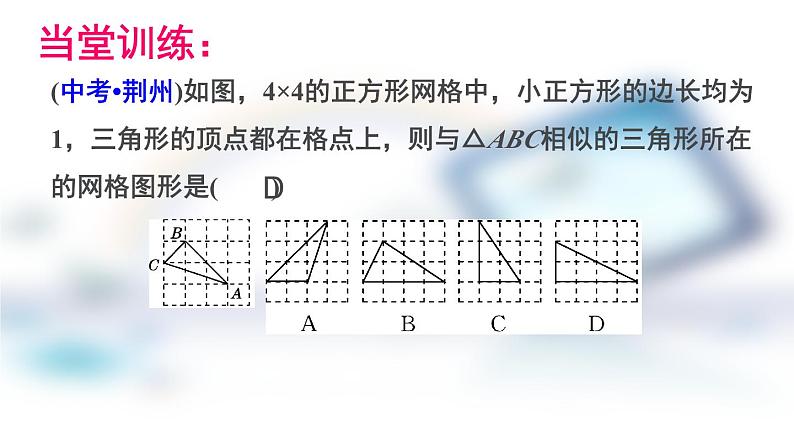
(中考•荆州)如图，4×4的正方形网格中，小正方形的边长均为1，三角形的顶点都在格点上，则与△ABC相似的三角形所在的网格图形是(　　)
探究： 两边对应成比例且夹角相等，两三角形相似
类似于判定三角形全等的SAS方法，能不能用两边和夹角来判定两个三角形相似呢？事实上，我们有“两边成比例且夹角相等的两个三角形相似”的定理它的证明思路与证明“三边成比例两三角形相似”的定理思路一样，请同学们课后自己证明
两边对应成比例且夹角相等，两三角形相似
∵A′B′:AB=A′C′:AC,∠A=∠A′
∴△A′B′C′∽△ABC
如果两个三角形两边成比例，但对应相等的角不是两条对应边的夹角，那么两个三角形是否相似呢？画一画，量一量.
探究两边成比例且非夹角相等的两个三角形的关系
AB:DE=AC:DF, ∠C= ∠F
如果两个三角形两边对应成比例，但对应相等的角不是两条对应边的夹角，那么两个三角形不一定相似.注意：对应相等的角一定要是两条对应边的夹角.
1、根据下列条件，判断△ABC与△A´B´C´是否相似，并说明理由：
(1) ∠A=120°， AB=3cm，AC=6cm, ∠A´=120°，A´B´=6cm，A´C´=12cm.
∴A′B′:AB=A′C′:AC,又∠A=∠A′= 120°
解：∵A′B′:AB=2 A′C′:AC=2,
(2) AB=4cm ，BC =6cm ，AC =8cm, A´B´=12cm ，B´C´=18cm ，A´C´=21cm
  2、如图，△ABC与△ADE都是等腰三角形，AD=AE，AB=AC，∠DAB=∠CAE.求证：△ABC∽△ADE.