数学九年级上册22.1 一元二次方程教案及反思

这是一份数学九年级上册22.1 一元二次方程教案及反思，共4页。教案主要包含了知识与技能，过程与方法，情感态度，教学重点，教学难点等内容，欢迎下载使用。
第2课时 用因式分解法解一元二次方程※教学目标※【知识与技能】理解并掌握因式分解法，并能灵活运用因式分解法解一元二次方程.【过程与方法】经历因式分解法的探究过程，使学生能探究并归纳出因式分解法.【情感态度】学生通过观察、分析、讨论与交流等活动，进一步增强与他人交流的能力.【教学重点】理解并掌握因式分解法，并能灵活运用因式分解法解一元二次方程.【教学难点】因式分解法的适当选用.※教学过程※一、复习引入试用两种方法解方程方法一：先移项,得再直接开平方,得所以原方程的解是方法二：将方程左边用平方差公式分解因式,得必有解这两个一元一次方程,得所以原方程的解是二、探索新知1.解一元二次方程的基本思想就是通过降次将二次方程转化为一次方程来解.对于下列方程：不用直接开平方法，你能把它们转化为两个一次方程，进而求出它们的解吗？解：（1）将方程左边用平方差公式分解因式,得所以所以(2)将方程左边用平方差公式分解因式,得所以所以2.因式分解法当一元二次方程的一边为零，而另一边能分解成两个一次因式乘积的形式时，可令每个因式分别为零，通过解这两个一元一次方程的方法来求此一元二次方程的解.这种解一元二次方程的方法叫做因式分解法.【例1】  用因式分解法解下列方程：分析：提公因式法是因式分解法的常用方法之一.解：（1）方程左边分解因式,得所以(2)移项，得方程左边分解因式,得所以【例2】  用因式分解法解下列方程：分析：运用公式法是因式分解法的基本方法之一，其中(1)、（2）运用平方差公式，（3）运用完全平方公式.解：（1）将方程左边运用平方差公式分解因式,得所以(2)将方程左边运用平方差公式分解因式,得整理,得所以(3)将方程左边运用完全平方公式分解因式,得三、巩固练习用因式分解法解下列方程:答案：四、应用拓展【例3】  解下列方程：分析：（1）可变形后用直接开平方法求解,（2）可用因式分解法求解.解：（1）变形,得直接开平方,得所以(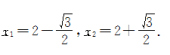2)将方程左边分解因式,得即所以【例4】  小张和小林一起解方程小张将方程左边分解因式，得小林的解法是这样的：移项，得方程两边都除以小林说：“我的方法多简便！”可另一个根哪里去了？小林的解法对吗？你能解开这个谜吗？解：小林的解法不对.原因在于等式左右两边都除以时，没有考虑的值是否为0,当时，解得x=6;而当时，左边=右边，此时在用因式分解法解方程时，通常把等式的一边化为0后，再进行求解.五、归纳小结1.因式分解法把一元二次方程化为两个一元一次方程来解，体现了“降次”的思想.2.因式分解法解一元二次方程的理论依据是两个因式的积等于零，那么这两个因式中至少有一个等于零，即3.因式分解法的关键是掌握分解因式的两种基本方法：提公因式法和运用公式法.※课后作业※教材第25页练习（1）、（2）、（3）、（4）题.