第22章 一元二次方程小结 华师大版数学九年级上册教案



章末小结

※教学目标※

【知识与技能】

1.进一步理解一元二次方程的定义，一般形式以及各项系数.

2.进一步深化理解一元二次方程的四种解法，能灵活运用四种解法解一元二次方程.

3.进一步理解根的判别式及其应用、根与系数的关系及其应用，能够运用它们去解决实际问题，综合性问题.

4.进一步加强列方程解应用题的能力，特别是增长率问题、几何图形问题.

【教学重点】

对一元二次方程的理解，掌握一元二次方程的四种解法以及一元二次方程解决实际应用问题.

【教学难点】

一元二次方程根的判别式的应用和根与系数的关系的应用.

※教学过程※

一、知识体系图解

二、知识专题复习

专题一  巧用一元二次方程根的定义解题

【例1】  若0是关于x的方程的解，求实数m的值，并讨论此方程解的情况.

分析：此方程只是说关于x的方程，并没有说明此方程是几次方程，这需由m的值来确定它的次数.因此应分m-2=0和m-2≠0两种情况讨论.

解：因为x=0是此方程的根，所以代入得

当m-2=0,即m=2时，此方程是一元一次方程3x=0,所以x=0.

当m-2≠0，即m≠2时，此方程是一元二次方程

所以此方程的两个解为0,

【归纳拓展】

（1）求一元二次方程中的某一个字母的取值范围时，依据一元二次方程的定义，应使这个字母或含这个字母的代数式的值同时满足两条：二次项的系数不等于0且未知数的最高次数是2.

（2）已知一元二次方程的根求方程中未知字母系数的值时，所求出的字母值也应满足两条：二次项的系数不等于0且未知数的最高次数是2.

【练习】

1.已知关于x的一元二次方程的一个根是0，求m的值.

2.在关于x的方程中，要使这个方程满足下列条件，则m的值分别为多少？

（1）是一元二次方程；（2）是一元一次方程.

答案：1.m=-   2.(1)m=-2  (2)m=2

专题二  一元二次方程的解法技巧

分析：选择恰当的方法是快速解方程的有效途径.

解：（1）直接开平方，得

所以方程的解为

（2）由题意，得x-1=0或2x+5=0,

所以方程的解为

(3)整理，得

所以方程的解为

（4）化为一般式，得

所以

所以方程的解为

【归纳拓展】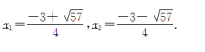

在解一元二次方程时，要观察方程的结构特点，在没给出解法要求时，解法选择的顺序是直接开平方法、因式分解法、公式法.配方法用得较少，但若二次项系数为1，一次项系数为偶数时，用配方法也比较简单.

【练习】

用适当的方法解下列方程：

答案：

专题三  一元二次方程的应用

【例3】  某拖拉机厂，今年一月份生产出一批甲、乙两种新型拖拉机，其中乙型16台，从二月份起，甲型每月增产10台，乙型每月按相同的增长率逐月递增，又知二月份甲、乙两种型号的产量比是3:2，三月份甲、乙两种型号的产量之和为65台，求乙型拖拉机每月的增长率及甲型拖拉机一月份的产量.

分析：本题直接要求的未知数有两个，间接未知量有好几个，但起制约作用并且可以承上启下的是二月份甲、乙两型的产量，因此可以采取间接设元的方法.

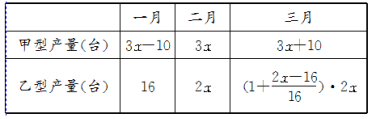
解：设二月份生产甲型拖拉机为3x台，则根据题意可得

解得(不合题意，舍去).

乙型拖拉机每月的增长率为

甲型拖拉机一月份的产量为3x-10=20(台)

答：乙型拖拉机每月增长率为25%，甲型拖拉机一月份的产量为20台.

【归纳拓展】

用一元二次方程能解决的问题涉及实际生活的各个方面，题型新颖，解法灵活，综合性强.常见的题型有增长（降低）率问题、利润问题、形积问题等.

【练习】

某商场以每件280元的价格购进一批商品，当每件商品售价为360元时，每月可售出60件，为了扩大销售，商场决定采取适当降价的方式促销，经调查发现，如果每件商品降价1元，那么商场每月就可以多售出5件.

（1）降价前商场每月销售该商品的利润是多少元？

（2）要使商场每月销售这种商品的利润达到7200元，且更有利于减少库存，则每件商品应降价多少元？

答案：（1）60×（360-280）=4800（元）.∴降价前商场每月销售该商品的利润是4800元.

（2）设每件商品应降价x元，根据题意，得（360-x-280）(5x+60)=7200.解得因为要求有利于减少库存，且降价越多，销售的数量越多，所以取x=60,即每件商品应降价60元.

专题四  一元二次方程根的判别式与根与系数的关系

【例4】  已知关于x的方程

（1）求证：方程有两个不相等的实数根.

（2）当m为何值时，方程的两根互为相反数？并求出此时方程的解.

分析：（1）要证一元二次方程有两个不相等的实数根，只需说明Δ>0即可.（2）两根互为相反数，说明两实根之和为零.

（1）证明：因为

所以，无论m取何值,Δ>0恒成立.

所以，方程有两个不相等的实数根.

（2）解：因为方程的两根互为相反数，所以

根据方程的根与系数的关系，得

解得m=-2.

所以原方程可化为解得

【归纳拓展】

在实数范围内运用一元二次方程根与系数的关系时，必须注意Δ≥0这个前提条件，而应用判别式Δ的前提条件是二次项的系数a≠0.因此，解题时要注意分析题中有没有隐含Δ≥0,a≠0.

在具体解题时，可先利用根与系数的关系，求出字母系数的值，然后代入判别式进行检验，把使判别式小于零的值舍去.要注意，只求出一个值，也要检验.

【练习】

已知关于x的方程有两个不相等的实数根.

（1）求k的取值范围；

（2）是否存在实数k，使方程两实数根互为相反数？

答案：（1）k<且k≠0  （2）实数k不存在

※课后作业※

教材第45页复习题.