7年级上册第二章单元检测卷

单元检测卷

时间：120分钟　　　　　满分：120分

一、选择题(每小题3分，共30分)　　　　　　　　　　　　　　　　　　

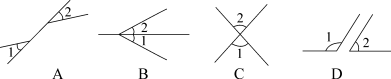
1．下列图形中，∠1与∠2互为对顶角的是(　　)

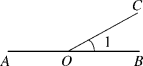
2．如图，O是直线AB上一点，若∠1＝26°，则∠AOC的度数为(　　)

A．154°         B．144°        C．116°        D．26°或154°

 第2题图　                  第3题图

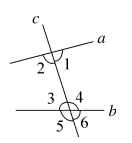
3．如图，已知直线a，b被直线c所截，那么∠1的同旁内角是(　　)

A．∠3            B．∠4            C．∠5            D．∠6

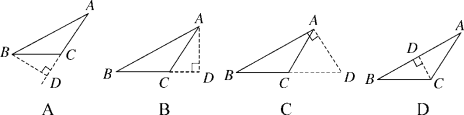
4．下列作图能表示点A到BC的距离的是(　　)

5．如图，下列条件：①∠1＝∠3；②∠2＝∠3；③∠4＝∠5；④∠2＋∠4＝180°中，能判断直线l1∥l2的有(　　)

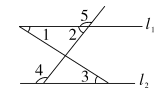
A．1个          B．2个             C．3个           D．4个

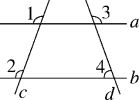
6．如图，直线a，b与直线c，d相交，已知∠1＝∠2，∠3＝110°，则∠4的度数为(　　)

A．70°            B．80°          C．110°           D．100°

第6题图　                      第7题图

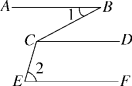
7．如图，AB∥CD，CD∥EF，则∠BCE等于(　　)

A．∠2－∠1                    B．∠1＋∠2

C．180°＋∠1－∠2              D．180°－∠1＋∠2

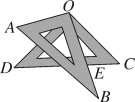
8．如图，将一副三角板叠放在一起，使直角的顶点重合于点O，AB∥OC，DC与OB交于点E，则∠DEO的度数为(　　)

A．85°             B．70°            C．75°             D．60°

第8题图                        第9题图

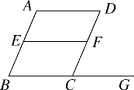
9．如图，E，F分别是AB，CD上的点，G是BC的延长线上一点，且∠B＝∠DCG＝∠D，则下列结论不一定成立的是(　　)

A．∠AEF＝∠EFC               B．∠A＝∠BCF

C．∠AEF＝∠EBC               D．∠BEF＋∠EFC＝180°

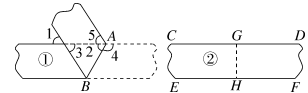
10．一次数学活动中，检验两条完全相同的纸带①、②的边线是否平行，小明和小丽采用两种不同的方法：小明把纸带①沿AB折叠，量得∠1＝∠2＝50°；小丽把纸带②沿GH折叠，发现GD与GC重合，HF与HE重合．则下列判断正确的是(　　)

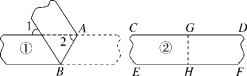
A．纸带①的边线平行，纸带②的边线不平行

B．纸带①的边线不平行，纸带②的边线平行

C．纸带①、②的边线都平行

D．纸带①、②的边线都不平行

二、填空题(每小题3分，共24分)

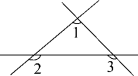
11．如图，∠1和∠2是________角，∠2和∠3是________角．

12．如图是李晓松同学在运动会跳远比赛中最好的一跳，甲、乙、丙三名同学分别测得PA＝5.52米，PB＝5.37米，MA＝5.60米，那么他的跳远成绩应该为________米．

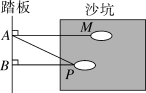
    第12题图　　                   第13题图

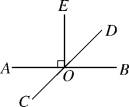
13．如图，直线AB，CD交于点O，OE⊥AB，OD平分∠BOE，则∠AOC＝________°.

14．如图，条件：____________可使AC∥DF；条件：____________可使AB∥DE(每空只填一个条件)．

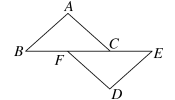
第14题图                           第15题图

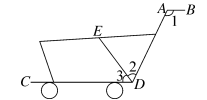
15．如图是超市里的购物车，扶手AB与车底CD平行，∠2比∠3大10°，∠1是∠2的倍，则∠2的度数是________．

16．一个安全用电标识如图①所示，此标识可以抽象为图②中的几何图形，其中AB∥CD，ED∥BF，点E、F在线段AC上．若∠A＝∠C＝17°，∠B＝∠D＝50°，则∠AED的度数为________．

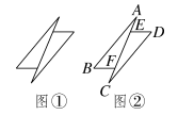
第16题图　　                    　　第17题图

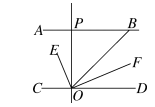
17．如图，AB∥CD，OE平分∠BOC，OF⊥OE，OP⊥CD，∠ABO＝a°.有下列结论：①∠BOE＝(180－a)°；②OF平分∠BOD；③∠POE＝∠BOF；④∠POB＝2∠DOF.其中正确的结论是________(填序号)．

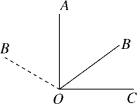
18．已知OA⊥OC，∠AOB∶∠AOC＝2∶3，则∠BOC的度数为________．

三、解答题(共66分)

19．(7分)已知一个角的余角比它的补角的还小55°，求这个角的度数．

20．(7分)用直尺和圆规作图：已知∠1，∠2，求作一个角，使它等于∠1＋2∠2.

21.(8分)如图，DG⊥BC，AC⊥BC，FE⊥AB，∠1＝∠2，试说明：CD⊥AB.

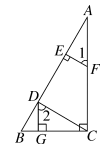
解：∵DG⊥BC，AC⊥BC(已知)，

∴∠DGB＝∠ACB＝90°(垂直定义)，

∴DG∥AC(__________________________)，

∴∠2＝∠________(____________________)．

∵∠1＝∠2(已知)，

∴∠1＝∠________(等量代换)，

∴EF∥CD(________________________)，

∴∠AEF＝∠________(__________________________)．

∵EF⊥AB(已知)，

∴∠AEF＝90°(________________)，

∴∠ADC＝90°(________________)，

∴CD⊥AB(________________)．

22．(8分)如图，直线AB，CD相交于点O，OE平分∠BOD，OF平分∠COB，∠AOD∶∠DOE＝4∶1，求∠AOF的度数．

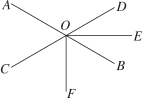
23．(10分)如图，已知直线l1∥l2，A，B分别是l1，l2上的点，l3和l1，l2分别交于点C，D，P是线段CD上的动点(点P不与C，D重合)．

(1)若∠1＝150°，∠2＝45°，求∠3的度数；

(2)若∠1＝α，∠2＝β，用α，β表示∠APC＋∠BPD.

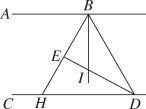
24．(12分)如图，已知BE平分∠ABD，DE平分∠BDC，且∠EBD＋∠EDB＝90°.

(1)试说明：AB∥CD；

(2)H是BE延长线与直线CD的交点，BI平分∠HBD，写出∠EBI与∠BHD的数量关系，并说明理由．

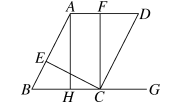
25．(14分)如图，已知AB∥CD，AD∥BC，∠DCE＝90°，点E在线段AB上，∠FCG＝90°，点F在直线AD上，∠AHG＝90°.

(1)找出图中与∠D相等的角，并说明理由；

(2)若∠ECF＝25°，求∠BCD的度数；

(3)在(2)的条件下，点C(点C不与B，H两点重合)从点B出发，沿射线BG的方向运动，其他条件不变，求∠BAF的度数．

参考答案与解析

1．C　2.A　3.B　4.B　5.C　6.A　7.C　8.C　9.C

10．B　解析：如图①，∵∠1＝∠2＝50°，∴∠3＝∠1＝50°，∠4＝180°－∠2＝130°.由折叠可知∠4＝∠2＋∠5，∴∠5＝∠4－∠2＝80°.∵∠3≠∠5，∴纸带①的边线不平行．如图②，∵GD与GC重合，HF与HE重合，∴∠CGH＝∠DGH＝90°，∠EHG＝∠FHG＝90°，∴∠CGH＋∠EHG＝180°，∴纸带②的边线平行．故选B.

11．同位　同旁内　12.5.37　13.45

14．∠ACB＝∠EFD　∠B＝∠E

15．55°　16.67°　17.①②③

18．30°或150°　解析：∵OA⊥OC，∴∠AOC＝90°.∵∠AOB∶∠AOC＝2∶3，∴∠AOB＝60°.如图，∠AOB的位置有两种情况：一种是在∠AOC内，一种是在∠AOC外．(1)当在∠AOC内时，∠BOC＝90°－60°＝30°；(2)当在∠AOC外时，∠BOC＝90°＋60°＝150°.综上可知，∠BOC的度数为30°或150°.

19．解：设这个角的度数为x，依题意有(180°－x)－55°＝90°－x，(4分)解得x＝75°.故这个角的度数为75°.(7分)

20．解：略．(7分)

21．解：同位角相等，两直线平行　ACD　两直线平行，内错角相等　ACD　同位角相等，两直线平行(4分)　ADC　两直线平行，同位角相等　垂直的定义　等量代换　垂直的定义(8分)

22．解：∵OE平分∠BOD，∴∠DOE＝∠EOB.(2分)又∵∠AOD∶∠DOE＝4∶1，∠AOD＋∠DOE＋∠EOB＝180°，∴∠DOE＝∠EOB＝30°，∠AOD＝120°，∴∠COB＝∠AOD＝120°.(5分)∵OF平分∠COB，∴∠BOF＝∠COB＝60°，∴∠AOF＝180°－∠BOF＝180°－60°＝120°.(8分)

23．解：(1)过点P向右作PE∥l1.∵l1∥l2，∴l1∥PE∥l2，∴∠1＋∠APE＝180°，∠2＝∠BPE.(2分)∵∠1＝150°，∠2＝45°，∴∠APE＝180°－∠1＝180°－150°＝30°，∠BPE＝∠2＝45°，∴∠3＝∠APE＋∠BPE＝30°＋45°＝75°.(6分)

(2)由(1)知∠1＋∠APE＝180°，∠2＝∠BPE.∵∠1＝α，∠2＝β，∴∠APB＝∠APE＋∠BPE＝180°－∠1＋∠2＝180°－α＋β，(8分)∴∠APC＋∠BPD＝180°－∠APB＝180°－(180°－α＋β)＝α－β.(10分)

24．解：(1)∵BE平分∠ABD，DE平分∠BDC，∴∠ABD＝2∠EBD，∠BDC＝2∠EDB.(3分)∵∠EBD＋∠EDB＝90°，∴∠ABD＋∠BDC＝2(∠EBD＋∠EDB)＝180°，∴AB∥CD.(6分)

(2)∠EBI＝∠BHD.(8分)理由如下：∵AB∥CD，∴∠ABH＝∠EHD.(10分)∵BI平分∠EBD，∴∠EBI＝∠EBD＝∠ABH＝∠BHD.(12分)

25．解：(1)与∠D相等的角为∠DCG，∠ECF，∠B.(1分)理由如下：∵AD∥BC，∴∠D＝∠DCG.∵∠FCG＝90°，∠DCE＝90°，∴∠ECF＝∠DCG＝∠D.∵AB∥DC，∴∠B＝∠DCG＝∠D，∴与∠D相等的角为∠DCG，∠ECF，∠B.(4分)

(2)∵∠ECF＝25°，∠DCE＝90°，∴∠FCD＝65°.又∵∠BCF＝90°，∴∠BCD＝65°＋90°＝155°.(7分)

(3)分两种情况进行讨论：①如图a，当点C在线段BH上时，点F在DA的延长线上，此时∠ECF＝∠DCG＝∠B＝25°.∵AD∥BC，∴∠BAF＝∠B＝25°；(10分)②如图b，当点C在BH的延长线上时，点F在线段AD上．∵∠B＝25°，AD∥BC，∴∠BAF＝180°－25°＝155°.综上所述，∠BAF的度数为25°或155°.(14分)