

数学八年级上册17.5 反证法随堂练习题
展开![]() 17.5反证法同步练习-冀教版数学八年级上册
17.5反证法同步练习-冀教版数学八年级上册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列说法中:①-2是4的一个平方根;②0的平方根和算术平方根都是0;③![]() 的立方根是4;④近似数
的立方根是4;④近似数![]() 精确到百分位;⑤用反证法证明“若
精确到百分位;⑤用反证法证明“若![]() ,则
,则![]() ”时,首先假设“
”时,首先假设“![]() ”,正确的有( )
”,正确的有( )
A.1个 B.2个 C.3个 D.4个
2.用反证法证明“直角三角形的两个锐角至少有一个角不大于![]() ”时,应假设( )
”时,应假设( )
A.两个锐角都大于![]() B.两个锐角都小于
B.两个锐角都小于![]()
C.两个锐角都不小于![]() D.一个锐角大于
D.一个锐角大于![]() ,另一个锐角小于
,另一个锐角小于![]()
3.已知![]() 中,
中,![]() ,求证:
,求证:![]() ,运用反证法证明这个结论,第一步应先假设( )成立
,运用反证法证明这个结论,第一步应先假设( )成立
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.用反证法证明命题“四边形中至少有一个角是钝角或直角”,应先假设( )
A.四边形中没有一个角是钝角或直角
B.四边形中至多有一个钝角或直角
C.四边形中没有一个角是锐角
D.四边形中没有一个角是钝角
5.用反证法证明:“直角三角形至少有一个锐角不小于45°”时,应先假设( )
A.直角三角形的每个锐角都小于45°
B.直角三角形有一个锐角大于45°
C.直角三角形的每个锐角都大于45°
D.直角三角形有一个锐角小于45°
6.公元前5世纪,毕达哥拉斯学派中的一名成员希伯索斯发现了无理数![]() ,导致了第一次数学危机.
,导致了第一次数学危机.![]() 是无理数的证明如下:
是无理数的证明如下:
假设![]() 是有理数,那么它可以表示成
是有理数,那么它可以表示成![]() (p与q是互质的两个正整数).于是
(p与q是互质的两个正整数).于是![]() ,所以,
,所以,![]() .于是
.于是![]() 是偶数,进而q是偶数.从而可设
是偶数,进而q是偶数.从而可设![]() ,所以
,所以![]() ,
,![]() ,于是可得p也是偶数.这与“p与q是互质的两个正整数”矛盾,从而可知“
,于是可得p也是偶数.这与“p与q是互质的两个正整数”矛盾,从而可知“![]() 是有理数”的假设不成立,所以
是有理数”的假设不成立,所以![]() 是无理数.
是无理数.
这种证明“![]() 是无理数”的方法是( )
是无理数”的方法是( )
A.综合法 B.反证法 C.举反例法 D.数学归纳法
7.利用反证法证明“x>2”,应先假设( )
A.x≤2 B.x<2 C.x≥2 D.x≠2
8.△ABC中,![]() 、
、![]() 、
、![]() 的对边分别是a、b、c,
的对边分别是a、b、c,![]() ,
,![]() ,
,![]() ,则下列结论不正确的是( )
,则下列结论不正确的是( )
A.△ABC是直角三角形,且AC为斜边 B.△ABC是直角三角形,且![]()
C.△ABC的面积是60 D.△ABC是直角三角形,且![]()
9.用反证法证明:三角形三内角至少有一个不小于60°时,应假设( )
A.三个角都大于60° B.三个角都小于60°
C.三个角都不大于60° D.三个角都不小于60°
10.说明命题“等腰三角形腰上的高小于腰”是假命题的反例可以是( )
A.等腰直角三角形
B.等边三角形
C.含30°的直角三角形
D.顶角为45°的等腰三角形
二、填空题
11.用反证法证明“多边形中至少有三个锐角”,第一步应假设 .
12.命题:“三角形中最多只有一个内角是直角”,用反证法证明时第一步需要假设
13.用反证法证明“a<|a|”,求证:a必为负数.
证明:假设a不是负数,那么a是 或a是 .
(1)如果a是零,那么a=|a|,这与题设矛盾,所以a不可能是零;
(2)如果a是 ,那么a=|a|,这与 矛盾,所以a不可能是 . 综合(1)和(2),知a不可能是 ,也不可能是 . 所以a必为负数.
14.利用反证法证明“在△ABC中,∠A>∠B,求证:BC>AC”时,第一步应假设: .
15.数学课上,同学提出如下问题:如何证明“两直线平行,同位角相等”?老师说这个证明可以用反证法完成,思路及过程如下:
如图1,我们想要证明“如果直线![]() ,
,![]() 被直线
被直线![]() 所截,
所截,![]() ,那么
,那么![]() ”
”
小贴士反证法不是直接从命题的已知得出结论,而是假设命题的结论不成立,由此经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立. 在某些情形下,反证法是很有效的证明方法。 |
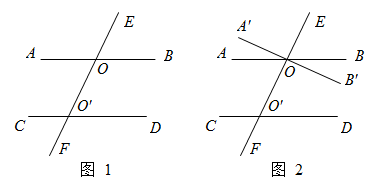 如图2,
如图2,
假设![]() ,过点
,过点![]() 作直线
作直线![]() ,使
,使![]() ,
,
依据基本事实(1) ,
可得![]() .这样过点
.这样过点![]() 就有两条直线
就有两条直线![]() ,
,![]() 都平行于直线
都平行于直线![]() ,
,
这与基本事实(2) 矛盾
说明![]() 的假设是不对的,于是有
的假设是不对的,于是有![]() .
.
16.三角形中至少有一个角不小于 度.
17.用反证法证明命题:“一个三角形中不能有两个直角”的过程归纳为以下三个步骤:
①∠A+∠B+∠C=90°+90°+∠C>180°,这与三角形内角和为180°相矛盾,则∠A=∠B=90°不成立;
②所以一个三角形中不能有两个直角;
③假设∠A,∠B,∠C中有两个角是直角,不妨设∠A=∠B=90°.
正确顺序的序号排列为 .
18.用反证法证明“![]() ”时,应假设 .
”时,应假设 .
19.要用反证法证明命题“三角形中必有一个内角小于或等于60°”,首先应假设 .
20.用反证法证明 “在△ABC中,如果∠B≠∠C,那么AB≠AC”,第一步应假设 .
三、解答题
21.判断下列命题是真命题还是假命题,请举出一个反例说明.
(1)若 ab =0,则 a +b =0;
(2)如果 a是无理数,b是无理数,则 a+b是无理数.
22.反证法是数学证明的一种重要方法.请将下面运用反证法进行证明的过程补全.
已知:在![]() 中,
中,![]() .求证:
.求证:![]() .
.
证明:假设_____________________.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
这与_______________________.
∴_______________________不成立.
∴![]()
参考答案:
1.C
2.A
3.A
4.A
5.A
6.B
7.A
8.D
9.B
10.A
11.同一多边形中最多有两个锐角.
12.三角形中最少有两个内角是直角
13. 正数 0 (2)正数 已知 正数 正数 0
14.假设BC≤AC
15. 同位角相等,两直线平行 过直线外一点有且只有一条直线与已知直线平行
16.60
17.③①②
18.a≥b
19.每一个内角都大于60°
20.AB=AC
21.(1)假命题;(2)假命题.
22.![]() ;三角形内角和定理或三角形的内角和等于
;三角形内角和定理或三角形的内角和等于![]() 相矛盾;此假设
相矛盾;此假设
初中第十七章 特殊三角形17.5 反证法综合训练题: 这是一份初中第十七章 特殊三角形17.5 反证法综合训练题,共5页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
数学八年级上册17.5 反证法综合训练题: 这是一份数学八年级上册17.5 反证法综合训练题,共3页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
数学八年级上册17.5 反证法课时练习: 这是一份数学八年级上册17.5 反证法课时练习,共4页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。













