冀教版九年级上册25.6 相似三角形的应用练习题

这是一份冀教版九年级上册25.6 相似三角形的应用练习题，共9页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
25.6相似三角形的应用同步练习-冀教版数学九年级上册学校:___________姓名：___________班级：___________考号：___________ 一、单选题1．现有一张Rt△ABC纸片，直角边BC长为12cm，另一直角边AB长为24cm．现沿BC边依次从下往上裁剪宽度均为3cm的矩形纸条，如图．已知剪得的纸条中有一张是正方形，则这张正方形纸条是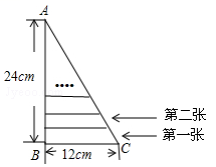（　　）A．第4张 B．第5张 C．第6张 D．第7张2．如图，一直角边长为4cm的等腰直角三角板在灯光照射下形成投影，该三角板与其投影的相似比为2∶3．则投影三角形的面积为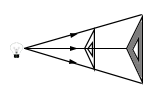（    ）A．36 B．18 C．16 D．203．“今有邑，东西七里，南北九里，各开中门，出东门一十五里有木，问：出南门几何步而见木？”这段话摘自《九章算术》．意思是说：如图，矩形城池ABCD，东边城墙AB长9里，南边城墙AD长7里，东门点E、南门点F分别是AB、AD中点，EG⊥AB，FH⊥AD，EG＝15里，HG经过A点，则FH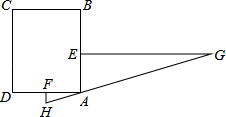＝（    ）A．1.2 里 B．1.5 里 C．1.05 里 D．1.02 里4．如图，在离某围端的6米处有一棵树，在某时刻2米长的竹竿垂直地面，太阳光下的影长为3米，此时，树的影子有一部分映在地面上，还有一部分影子映在墙上处，墙上的影高为4米，那么这棵树高约为（    ）A．6 B．8 C．9 D．105．如图，将△ABC沿着过AP中点D的直线折叠，使点A落在B C边上的A1处，称为第1次操作，折痕DE到BC的距离记为h1，还原纸片后，再将△ADE沿着过AD中点D1的直线折叠，使点A落在DE边上的A2处，称为第2次操作，折痕D1E1到BC的距离记为h2，按上述方法不断操作下去…经过第2018次操作后得到的折痕D2017E2017到BC的距离记为h2018，若h1=1，则h2018的值为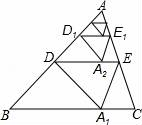（　　）A．2﹣ B． C．1﹣ D．2﹣6．凸透镜成像的原理如图所示，．若物体到焦点的距离与焦点到凸透镜中心线的距离之比为，则物体被缩小到原来的（    ）A． B． C． D．7．如图，树AB在路灯O的照射下形成投影AC，已知路灯高，树影，树AB与路灯O的水平距离，则树的高度AB长是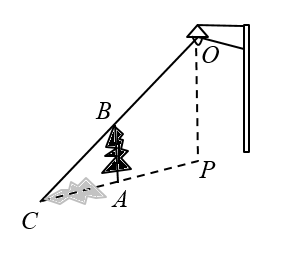（   ）A． B． C． D．8．为测量操场上旗杆的高度，小丽同学想到了物理学中平面镜成像的原理，她拿出随身携带的镜子和卷尺，先将镜子放在脚下的地面上，然后后退，直到她站直身子刚好能从镜子里看到旗杆的顶端E，标记好脚掌中心位置为B，测得脚掌中心位置B到镜面中心C的距离是50cm，镜面中心C距离旗杆底部D的距离为4m，如图所示．已知小丽同学的身高是1.54m，眼睛位置A距离小丽头顶的距离是4cm，则旗杆DE的高度等于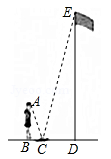（　　）A．10m B．12m C．12.4m D．12.32m9．某餐厅为了追求时间效率，推出一种液体“沙漏”免单方案（即点单完成后，开始倒转“沙漏”， “沙漏”漏完前，客人所点的菜需全部上桌，否则该桌免费用餐）．“沙漏”是由一个圆锥体和一个圆柱体相通连接而成．某次计时前如图（1）所示，已知圆锥体底面半径是，高是；圆柱体底面半径是，液体高是．计时结束后如图（2）所示，求此时“沙漏”中液体的高度为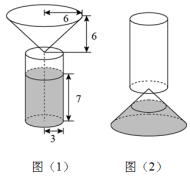（    ）A． B． C． D．10．如图，某校数学兴趣小组利用标杆BE测量学校旗杆CD的高度，标杆BE高1．5m，测得AB＝2m，BC＝14m，则旗杆CD高度是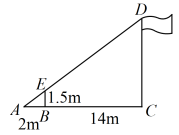（  ）  A．10.5m B．12mC．14m D．16m 二、填空题11．如图，身高的小超站在某路灯下，发现自己的影长恰好是，经测量，此时小超离路灯底部的距离是，则路灯离地面的高度是      ．12．如图，在同一时刻，小明测得他的影长为1米，距他不远处的一棵槟榔树的影长为5米，已知小明的身高为米，则这棵槟榔树的高是         米．  13．《孙子算经》是中国古代重要的数学著作，成书于约一千五百年前，其中有首歌谣：“今有竿不知其长，量得影长一丈五尺，立一标杆，长一尺五寸，影长五寸，问竿长几何？”意思就是：有一根竹竿不知道有多长，量出它在太阳下的影子长一丈五尺，同时立一根一尺五寸的小标杆（如图所示），它的影长五寸（提示：1丈＝10尺，1尺＝10寸），则竹竿的长为 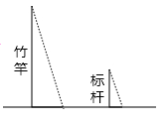    ．14．上小学五年级的小丽看见上初中的哥哥小勇用测树的影长和自己的影长的方法来测树高，她也学着哥哥的样子在同一时刻测得树的影长为5米，自己的影长为1米．要求得树高，还应测得    15．公共自行车车桩的截面示意图如图所示，AB⊥AD，AD⊥DC，点B，C在EF上，EF∥HG，EH⊥HG，AB＝80cm，AD＝24cm，BC＝25cm，EH＝4cm，则点A到地面的距离是    cm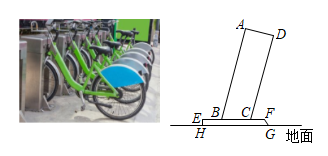．16．如图，某同学利用标杆BE测量教学楼的高度，已知标杆BE高1.5m，测得AB＝1.2m，BC＝12.8m，则教学楼CD的高度是      m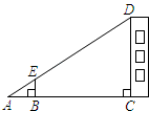．17．九年级（1）班课外活动小组利用标杆测量学校旗杆的高度，已知标杆高度，标杆与旗杆的水平距离，人的眼睛与地面的高度，人与标杆的水平距离，旗杆的高度为               m．18．小明欲测量一座古塔的高度，他站在该塔的影子上前后移动，直到他本身影子的顶端正好与塔的影子的顶端重叠，此时他距离该塔，已知小明的身高是，他的影长是．则塔高      ．19．汪老师要装修自己带阁楼的新居(如图为新居剖面图)，在建造客厅到阁楼的楼梯AC时，为避免上楼时墙角F碰头，设计墙角F到楼梯的竖直距离FG为1.75 m．他量得客厅高AB＝2.8 m，楼梯洞口宽AF＝2 m，阁楼阳台宽EF＝3 m．要使墙角F到楼梯的竖直距离FG为1.75 m，楼梯底端C到墙角D的距离CD是             m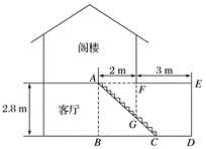．20．“跳眼法”是指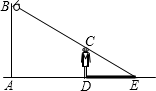用手指和眼睛估测距离的方法，步骤：第一步：水平举起右臂，大拇指紧直向上，大臂与身体垂直；第二步：闭上左眼，调整位置，使得右眼、大拇指、被测物体在一条直线上；第三步：闭上右眼，睁开左眼，此时看到被测物体出现在大拇指左侧，与大拇指指向的位置有一段横向距离，参照被测物体的大小，估算横向距离的长度；第四步：将横向距离乘以10（人的手臂长度与眼距的比值一般为10），得到的值约为被测物体离观测点的距离值．如图是用“跳眼法”估测前方一辆汽车到观测点距离的示意图，该汽车的长度大约为5米，则汽车到观测点的距离约为      米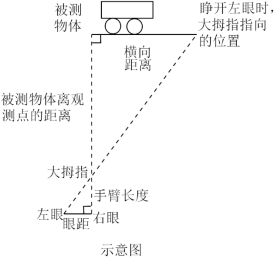． 三、解答题21．如图，在斜坡的顶部有一铁塔AB，B是CD的中点，CD是水平的，在阳光的照射下，塔影DE留在坡面上.若铁塔底座宽CD=12m，塔影长 m，小明和小华的身高都是1.6m，同一时刻小明站在点E处，影子在坡面上，小华站在平地上，影子也在平地上，两人的影长分别为2m和1m，求塔高AB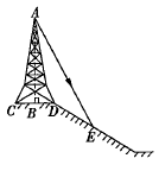．22．西安市的大雁塔又名“慈恩寺塔”，是国家级文物保护单位，玄奘为保存由天竺经丝绸之路带回长安的经卷主持修建了大雁塔，最初五层，后加盖至九层，是西安市的标志性建筑之一，某校社会实践小组为了测量大雁塔的高度，在地面上C处垂直于地面竖立了高度为2米的标杆CD，这时地面上的点E，标杆的顶端点D，大雁塔的塔尖点B正好在同一直线上，测得EC=4米，将标杆CD向后平移到点G处，这时地面上的点F，标杆的顶端点H，大雁塔的塔尖点B正好在同一直线上(点F，点G，点E，点C与塔底处的点A在同一直线上)，这时测得FG=6米，GC=53米，请你根据以上数据，计算大雁塔的高度AB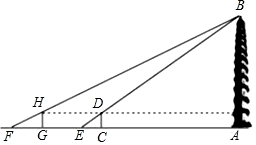．23．如图，在阳光下，身高1.7m的小明AB在地面上的影长BC为3.4m．在同一时刻，测得旗杆DE在地面的影长EF为24m，求旗杆DE的高度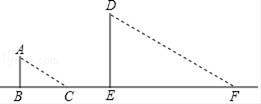．24．如图，一条河的两岸BC与DE互相平行，两岸各有一排景观灯(图中黑点代表景观灯)，每排相邻两景观灯的间隔都是10 m，在与河岸DE的距离为16 m的A处(AD⊥DE)看对岸BC，看到对岸BC上的两个景观灯的灯杆恰好被河岸DE上两个景观灯的灯杆遮住．河岸DE上的两个景观灯之间有1个景观灯，河岸BC上被遮住的两个景观灯之间有4个景观灯，求这条河的宽度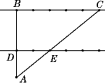．25．一位同学想利用有关知识测旗杆的高度，他在某一时刻测得高为的小木棒的影长为，但当他马上测量旗杆的影长时，因旗杆靠近一幢建筑物，影子不全落在地面上，有一部分影子在墙上，他先测得留在墙上的影子，又测地面部分的影长，你能根据上述数据帮他测出旗杆的高度吗？
参考答案：1．C2．B3．C4．B5．A6．A7．A8．B9．B10．B11．7.212．13．四丈五尺14．她自己的身高15．16．17.517．13.518．19．1.820．10021．塔高AB为24m.22．大雁塔的高度AB为55米．23．12米．24．这条河的宽度为24m.25．能．旗杆的高度为．