冀教版九年级上册26.4 解直角三角形的应用一课一练
展开![]() 26.4解直角三角形的应用同步练习-冀教版数学九年级上册
26.4解直角三角形的应用同步练习-冀教版数学九年级上册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,为了测量某建筑物AB的高度,在平地上C处测得建筑物顶端A的仰角为30°,沿CB方向前进16m到达D处,在D处测得建筑物顶端A的仰角为45°,则建筑物AB的高度等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.工地上有甲、乙二块铁板,铁板甲形状为等腰三角形,其顶角为![]() ,腰长为
,腰长为![]() ;铁板乙形状为直角梯形,两底边长分别为
;铁板乙形状为直角梯形,两底边长分别为![]() 、
、![]() ,且有一内角为
,且有一内角为![]() .现在我们把它们任意翻转,分别试图从一个直径为
.现在我们把它们任意翻转,分别试图从一个直径为![]() 的圆洞中穿过,结果是( )
的圆洞中穿过,结果是( )
A.甲板能穿过,乙板不能穿过 B.甲板不能穿过,乙板能穿过
C.甲、乙两板都能穿过 D.甲、乙两板都不能穿过
3.如果小丽在楼上点A处看到楼下点B处小明的俯角是35°,那么点B处小明看点A处小丽的仰角是( )
A.35° B.45° C.55° D.65°
4.如图,在距离铁轨200米处的![]() 处,观察由南宁开往百色的“和谐号”动车,当动车车头在
处,观察由南宁开往百色的“和谐号”动车,当动车车头在![]() 处时,恰好位于
处时,恰好位于![]() 处的北偏东
处的北偏东![]() 方向上,10秒钟后,动车车头到达
方向上,10秒钟后,动车车头到达![]() 处,恰好位于
处,恰好位于![]() 处西北方向上,则这时段动车的平均速度是( )米/秒.
处西北方向上,则这时段动车的平均速度是( )米/秒.

A.![]() B.
B.![]() C.200 D.300
C.200 D.300
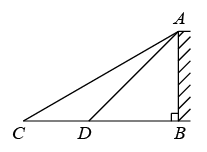
5.如图,王师傅在楼顶上A点处测得楼前一棵树CD的顶端C的俯角为60°,若水平距离BD=10 m,楼高AB=24 m,则树CD高约为( )

A.5 m B.6 m C.7 m D.8 m
6.如图所示,九(2)班的同学准备在坡度是1:2的斜坡上栽树,要求相邻两棵树之间的水平距离是![]() ,那么这两棵树在坡面上的距离
,那么这两棵树在坡面上的距离![]() 为( )
为( )

A.![]() B.9 C.10 D.
B.9 C.10 D.![]()
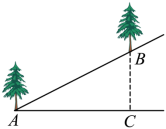
7.如图,在坡度为![]() 的山坡上种树,要求相邻两棵树之间的水平距离
的山坡上种树,要求相邻两棵树之间的水平距离![]() 为6米,则斜坡上相邻两树之间的坡面距离
为6米,则斜坡上相邻两树之间的坡面距离![]() 为( )
为( )
A.3米 B.![]() 米 C.
米 C.![]() 米 D.6米
米 D.6米
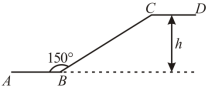
8.如图,是某超市一楼与二楼之间的阶梯式电梯示意图,其中![]() 、
、![]() 分别表示一楼、二楼地面的水平线,
分别表示一楼、二楼地面的水平线,![]() ,
,![]() 的长为
的长为![]() , 则乘电梯从点
, 则乘电梯从点![]() 到点
到点![]() 上升的高度
上升的高度![]() 是( )
是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进40海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海里C到航线AB的距离CD是( )
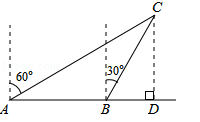
A.20海里 B.40海里 C.![]() 海里 D.
海里 D.![]() 海里
海里
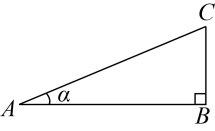
10.中国最长的索道为张家界天门山索道全长为7454米,若索道AC和地面AB的夹角为![]() ,则索道的落差BC可表示为( )
,则索道的落差BC可表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题
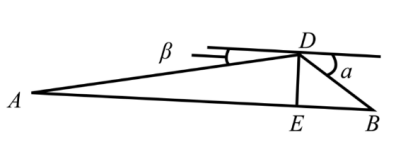
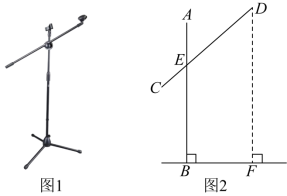
11.图![]() 为放在水平地面上的落地式话筒架实物图,图
为放在水平地面上的落地式话筒架实物图,图![]() 为其示意图,支撑杆
为其示意图,支撑杆![]() 垂直于地面
垂直于地面![]() ,活动杆
,活动杆![]() 固定在支撑杆上的点
固定在支撑杆上的点![]() 处,若
处,若![]() ,
,![]() ,
,![]() ,则活动杆端点
,则活动杆端点![]() 离地面的高度
离地面的高度![]()
![]() .(结果精确到
.(结果精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]() )
)
![]()
12.一物体沿坡度为1:8的山坡向上移动![]() 米,则物体升高了 米.
米,则物体升高了 米.
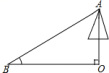
13.如图,为测量一棵与地面垂直的树![]() 的高度,在距离树的底端
的高度,在距离树的底端![]() 米的
米的![]() 处,测得树顶
处,测得树顶![]() 的仰角
的仰角![]() 为
为![]() ,则树
,则树![]() 的高度为 米(用三角函数表示)
的高度为 米(用三角函数表示)
14.如图,斜坡![]() 的坡度
的坡度![]() ,该斜坡的水平距离
,该斜坡的水平距离![]() 米,那么斜坡
米,那么斜坡![]() 的长等于 米.
的长等于 米.
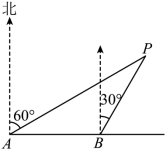
15.如图,海上有一灯塔P,位于小岛A北偏东![]() 方向上,一艘轮船从小岛A出发,由西向东航行24海里到达B处,这时测得灯塔P在北偏东
方向上,一艘轮船从小岛A出发,由西向东航行24海里到达B处,这时测得灯塔P在北偏东![]() 方向上,如果轮船不改变航向继续向东航行,当轮船到达灯塔P的正南方,此时轮船与灯塔P的距离是 海里.
方向上,如果轮船不改变航向继续向东航行,当轮船到达灯塔P的正南方,此时轮船与灯塔P的距离是 海里.
16.一条上山直道的坡度为![]() ,沿这条直道上山,在斜坡上每前进
,沿这条直道上山,在斜坡上每前进![]() 米所上升的高度为 米.(结果保留根号)
米所上升的高度为 米.(结果保留根号)
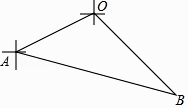
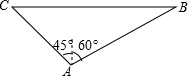
17.如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时10海里的速度航行,甲沿南偏西75°方向以每小时10![]() 海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.则甲船追赶乙船的速度为 海里/小时?
海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.则甲船追赶乙船的速度为 海里/小时?
18.离旗杆20米处的地方用测角仪测得旗杆顶的仰角为![]() , 如果测角仪高为1.5米.那么旗杆的高为 米(用含
, 如果测角仪高为1.5米.那么旗杆的高为 米(用含![]() 的三角函数表示).
的三角函数表示).
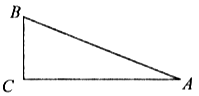
19.如图,一艘轮船在小岛A的北偏东60°方向且距小岛80海里的B处,沿正西方向航行一定时间后到达小岛的北偏西45°的C处,则该船航行的路程为 海里.
20.一个小球由地面沿着坡比1:2的坡面向上前进了5米,此时小球距离地面的高度为 米.
三、解答题
21.学完解直角三角形后,某数学兴趣小组准备用所学的知识测量河南郑州花园口某处黄河的宽度.他们制定了测量方案,并利用课余时间完成了实地测量.测量项目和测量数据如下表:
项目 | 测量花园口某处黄河的宽度 | |||||||||
成员 | 组长:××× 组员:××× ××× | |||||||||
测量工具 | 无人机(可测量无人机离水面的高度及俯角) | |||||||||
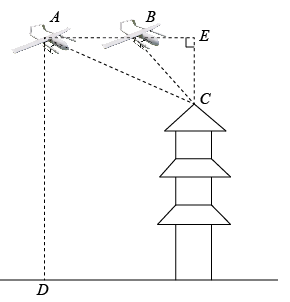
示意图 |
| |||||||||
测量数据 |
|
|
| |||||||
第一次 | 第二次 | 平均值 | 第一次 | 第二次 | 平均值 | 第一次 | 第二次 | 平均值 | ||
|
|
|
|
|
|
|
|
| ||
根据以上信息,解答下列问题:
(1)请利用上表中的测量数据,帮助该数学兴趣小组计算出花园口某处黄河的宽度![]() .
.
(结果保留整数参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
(2)有同学提出一个方案,直接利用无人机测量花园口某处黄河的宽度,由B处正上方水平匀速飞行到A处正上方,即可知道河面![]() 的宽度,请你分析该方案是否可行,并说明理由.
的宽度,请你分析该方案是否可行,并说明理由.
(3)该数学兴趣小组要写出一份完整的课题活动报告,除上表中的项目外,你认为还需要补充哪些项目?(写出一个即可)
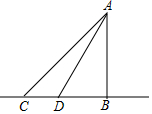
22.如图,有一铁塔AB,为了测量其高度,在水平面选取C,D两点,在点C处测得A的仰角为45°,距点C的10米D处测得A的仰角为60°,且C、D、B在同一水平直线上,求铁塔AB的高度(结果精确到0.1米,![]() ≈1.732)
≈1.732)
23.小颖的数学学习日记:x月x日:测量旗杆的高度.

(1)今天上午王老师要带我们去操场测量旗杆的高度,昨天我们小组设计了一个方案,方案如下:小亮拿着标杆垂直于地面放置,我和小聪用卷尺测量标杆、标杆的影长和旗杆的影长,如图1所示,标杆AB=a,影长BC=b,旗杆的影长DF=c,则可求得旗杆DE的高度为 .
(2)但今天测量时,阴天没有阳光,就不能用以上的方案了.如图2所示,王老师将升旗用的绳子拉直,使绳子的底端G刚好触到地面,用仪器测得绳子与地面的夹角为37°,然后又将绳子拉到一个0.5米高的平台上,拉直绳子使绳子上的H点刚好触到平台,剩余的绳子长度为5米,此时测得绳子与平台的夹角为54°,利用这些数据能求出旗杆DE的高度吗?(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75;sin54°≈0.8,cos54°≈0.58,tan54°≈1.45)请你回答小颖的问题.若能,请求出旗杆的高度;若不能,请说明理由.
24.2012年4月11日16时38分北苏门答腊西海岸发生里氏8.6级地震,并伴有海啸.山坡上有一棵与水平面垂直的大树,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示).已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=6m.
(1)求∠DAC的度数;
(2)求这棵大树折断前的高度?(结果精确到个位,参考数据:![]() ,
,![]() ,
,![]() )
)

25.“眉山水街”走红网络,成为全国各地不少游客新的打卡地!游客小何用无人机对该地一标志建筑物进行拍摄和观测,如图,无人机从![]() 处测得该建筑物顶端
处测得该建筑物顶端![]() 的俯角为24°,继续向该建筑物方向水平飞行20米到达
的俯角为24°,继续向该建筑物方向水平飞行20米到达![]() 处,测得顶端
处,测得顶端![]() 的俯角为45°,已知无人机的飞行高度为60米,则这栋建筑物的高度是多少米?(精确到0.1米,参考数据:
的俯角为45°,已知无人机的飞行高度为60米,则这栋建筑物的高度是多少米?(精确到0.1米,参考数据:![]() ,
,![]() ,
,![]() )
)
参考答案:
1.A
2.A
3.A
4.A
5.C
6.A
7.B
8.C
9.C
10.A
11.![]()
12.1.
13.![]()
14.![]() ;
;
15.![]()
16.![]()
17.![]()
18.1.5 +20tan![]()
19.(40+40![]() )
)
20.![]()
21.(1)![]()
(2)该方案理论上可行,理由:飞机由B处上方水平匀速飞行到A处上方的路程就等于AB的长度,故可行.(答案不难一,合理即可)
(3)数学兴趣小组要完成一份完整的课题活动报告除上表中的项目外,还需要补充计算结果.(答案不唯一,合理即可)
22.电视塔AB的高度约23.7米.
23.(1)![]() ;(2)能,10.5m.
;(2)能,10.5m.
24.(1)75°;(2)15米.
25.![]()
初中数学冀教版九年级上册26.4 解直角三角形的应用随堂练习题: 这是一份初中数学冀教版九年级上册26.4 解直角三角形的应用随堂练习题,共8页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
冀教版26.4 解直角三角形的应用课后复习题: 这是一份冀教版26.4 解直角三角形的应用课后复习题,共9页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
冀教版九年级上册第26章 解直角三角形26.4 解直角三角形的应用课后测评: 这是一份冀教版九年级上册第26章 解直角三角形26.4 解直角三角形的应用课后测评,共10页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。