专题九 最值模型-备战2024年高考数学之解密几何体的外接球与内切球十大模型命题点对点突破

这是一份专题九 最值模型-备战2024年高考数学之解密几何体的外接球与内切球十大模型命题点对点突破，文件包含专题九最值模型原卷版docx、专题九最值模型解析版docx等2份试卷配套教学资源，其中试卷共10页， 欢迎下载使用。
专题九　最值模型 【方法总结】最值问题的解法有两种方法：一种是几何法，即在运动变化过程中得到最值，从而转化为定值问题求解．另一种是代数方法，即建立目标函数，从而求目标函数的最值．【例题选讲】[例]　(1)已知三棱锥P－ABC的顶点P，A，B，C在球O的球面上，△ABC是边长为的等边三角形，如果球O的表面积为36π，那么P到平面ABC距离的最大值为________．答案　3＋2　解析　依题意，边长是的等边△ABC的外接圆半径r＝·＝1.∵球O的表面积为36π＝4πR2，∴球O的半径R＝3，∴球心O到平面ABC的距离d＝＝2，∴球面上的点P到平面ABC距离的最大值为R＋d＝3＋2．(2)在四面体ABCD中，AB＝1，BC＝CD＝，AC＝，当四面体ABCD的体积最大时，其外接球的表面积为(　　)A．2π　　　　　　　　B．3π　　　　　　　　C．6π　　　　　　　　D．8π答案　C　解析　∵AB＝1，BC＝，AC＝，由勾股定理可得AB2＋AC2＝BC2，所以△ABC是以BC为斜边的直角三角形，且该三角形的外接圆直径为BC＝，当CD⊥平面ABC时，四面体ABCD的体积取最大值，此时，其外接球的直径为2R＝＝，因此，四面体ABCD的外接球的表面积为4πR2＝π×(2R)2＝6π．故选C．(3)已知四棱锥S－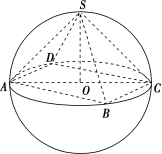ABCD的所有顶点在同一球面上，底面ABCD是正方形且球心O在此平面内，当四棱锥的体积取得最大值时，其表面积等于16＋16，则球O的体积等于(　　)A．　　　　　　　　B．　　　　　　　　C．　　　　　　　　D．答案　D　解析　由题意得，当四棱锥的体积取得最大值时，该四棱锥为正四棱锥．因为该四棱锥的表面积等于16＋16，设球O的半径为R，则AC＝2R，SO＝R，如图，所以该四棱锥的底面边长AB＝R，则有(R)2＋4××R× ＝16＋16，解得R＝2，所以球O的体积是πR3＝π．故选D．(4)三棱锥A－BC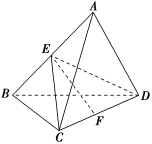D内接于半径为的球O中，AB＝CD＝4，则三棱锥A－BCD的体积的最大值为(　　)A．　　　　　　　　B．　　　　　　　　C．　　　　　　　　D．答案　C　解析　如图，过CD作平面ECD，使AB⊥平面ECD，交AB于点E，设点E到CD的距离为EF，当球心在EF上时，EF最大，此时E，F分别为AB，CD的中点，且球心O为EF的中点，所以EF＝2，所以Vmax＝××4×2×4＝，故选C．(5)已知正四棱柱的顶点在同一个球面上，且球的表面积为12π，当正四棱柱的体积最大时，正四棱柱的高为________．答案　8　解析　设正四棱柱的底面边长为a，高为h，球的半径为r，由题意知4πr2＝12π，所以r2＝3，又2a2＋h2＝(2r)2＝12，所以a2＝6－，所以正四棱柱的体积V＝a2h＝h，则V′＝6－h2，由V′>0，得0<h<2，由V′<0，得h>2，所以当h＝2时，正四棱柱的体积最大，Vmax＝8．【对点训练】1．三棱锥P－ABC的四个顶点都在体积为的球的表面上，底面ABC所在的小圆面积为16π，则该三棱锥的高的最大值为(　　)A．4　　　　　　　　B．6　　　　　　　　C．8　　　　　　　　D．102．(2015·全国Ⅱ)已知A，B是球O的球面上两点，∠AOB＝90°，C为该球面上的动点．若三棱锥O－ABC体积的最大值为36，则球O的表面积为(　　)A．36π　　　　　　　　B．64π　　　　　　　　C．144π　　　　　　　　D．256π3．已知点A，B，C，D均在球O上，AB＝BC＝，AC＝2．若三棱锥D－ABC体积的最大值为3，则球O的表面积为________．4．在三棱锥A－BCD中，AB＝1，BC＝，CD＝AC＝，当三棱锥A－BCD的体积最大时，其外接球的表面积为________．5．已知三棱锥D－ABC的所有顶点都在球O的球面上，AB＝BC＝2，AC＝2，若三棱锥D－ABC体积的最大值为2，则球O的表面积为(　　)A．8π　　　　　　　　B．9π　　　　　　　　C．　　　　　　　　D．6．三棱锥A－BCD的一条棱长为a，其余棱长均为2，当三棱锥A－BCD的体积最大时，它的外接球的表面积为(　　)A．　　　　　　　　B．　　　　　　　　C．　　　　　　　　D．7．已知三棱锥O－ABC的顶点A，B，C都在半径为2的球面上，O是球心，∠AOB＝120°，当△AOC与△BOC的面积之和最大时，三棱锥O－ABC的体积为(　　)A．　　　　　　　　B．　　　　　　　　C．　　　　　　　　D．8．(2018·全国Ⅲ)设A，B，C，D是同一个半径为4的球的球面上四点，△ABC为等边三角形且其面积为9，则三棱锥D－ABC体积的最大值为(　　)A．12　　　　　　　　B．18　　　　　　　　C．24　　　　　　　　D．549．已知球的直径SC＝4，A，B是该球球面上的两点，∠ASC＝∠BSC＝30˚，则棱锥S－ABC的体积最大为(　　)A．2　　　　　　　　B．　　　　　　　　C．　　　　　　　　D．210．四棱锥P－ABCD的底面为矩形，矩形的四个顶点A，B，C，D在球O的同一个大圆上，且球的表面积为16π，点P在球面上，则四棱锥P－ABCD体积的最大值为(　　)A．8　　　　　　　　B．　　　　　　　　C．16　　　　　　　　D．11．(2016·全国Ⅲ)在封闭的直三棱柱ABC－A1B1C1内有一个体积为V的球．若AB⊥BC，AB＝6，BC＝8，AA1＝3，则V的最大值是(　　)A．4π　　　　　　　　B．　　　　　　　　C．6π　　　　　　　　D．12．已知半径为1的球O中内接一个圆柱，当圆柱的侧面积最大时，球的体积与圆柱的体积的比值为________．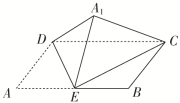13．如图，在矩形ABCD中，已知AB＝2AD＝2a，E是AB的中点，将△ADE沿直线DE翻折成△A1DE，连接A1C．若当三棱锥A1－CDE的体积取得最大值时，三棱锥A1－CDE外接球的体积为，则a＝(　　)A．2　　　　　　　　B．　　　　　　　　C．2　　　　　　　　D．414．已知三棱锥S－ABC的顶点都在球O的球面上，且该三棱锥的体积为2，SA⊥平面ABC，SA＝4，∠ABC＝120°，则球O的体积的最小值为________．