2022-2023学年北京市海淀区首都师大二附中八年级（下）期中数学试卷（含解析）

这是一份2022-2023学年北京市海淀区首都师大二附中八年级（下）期中数学试卷（含解析），共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年北京市海淀区首都师大二附中八年级（下）期中数学试卷
一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）
1. 下列二次根式中是最简二次根式的是(    )
A. 2 12 B. 4 C. 10 D. 12
2. 下列计算错误的是(    )
A. 3+2 2=5 2 B. 8÷2= 2 C. 2× 3= 6 D. 8− 2= 2
3. 在Rt△ABC中，∠ACB=90°，AB=5，AC=4，则BC的长为(    )
A. 3 B. 3或 7 C. 3或 41 D. 41
4. 一次函数y=−2x+3的图象上有两点A(1,y1)，B(−2,y2)，则y1与y2的大小关系是(    )
A. y1y2
5. 如图，把矩形ABCD沿EF对折后使两部分重合，若∠1=50°，则∠AEF=(    )
A. 100°
B. 105°
C. 110°
D. 115°
6. 下列命题中，是真命题的是(    )
A. 对角线相等的菱形是正方形
B. 对角线互相垂直的四边形是菱形
C. 对角线相等且互相垂直的四边形是矩形
D. 有一组对边相等，一组对角相等的四边形是平行四边形
7. 如图，平行四边形ABCD的周长是32cm，对角线AC与BD交于点O，AC⊥AB，E是BC中点，△AOD的周长比△AOB的周长多2cm，则AE的长度为(    )

A. 4 2cm B. 2 2cm C. 4.5cm D. 3.5cm
8. 在Rt△ABC中，∠ACB=90°，AC=BC=1，点Q在直线BC上，且AQ=2，则线段BQ的长为(    )
A. 3 B. 5
C. 3+1或 3−1 D. 5+1或 5−1
9. 如图，一次函数y=ax+b与y=cx+d的图象交于点P.下列结论：①bcx+d；④a+b=c+d；⑤c>d.所有正确结论的序号为(    )


A. ①②③ B. ①②④ C. ②③⑤ D. ②④⑤
10. 如图，在平面直角坐标系xOy中，菱形ABCD的边长为 10，点B的坐标为(0,1)，点C在第一象限，对角线BD与x轴平行．直线y=x+3与x轴、y轴分别交于点E，F.将菱形ABCD沿x轴向左平移m个单位，当点D落在△EOF的内部时(不包括三角形的边)，m的值可能是(    )


A. 4 B. 5 C. 6 D. 7
二、填空题（本大题共8小题，共24.0分）
11. 在函数y= 2x−1中，自变量x的取值范围是          ．
12. 直线y=13x经过第______ 象限．
13. 已知一次函数y=(k+3)x−2，y随x的增大而减小，则k的取值范围是______ ．
14. 如图，菱形ABCD中，AB=10，AC，BD交于点O，若E是边AD的中点，∠ABO=32°，则OE的长等于______ ，∠ADO的度数为______ ．
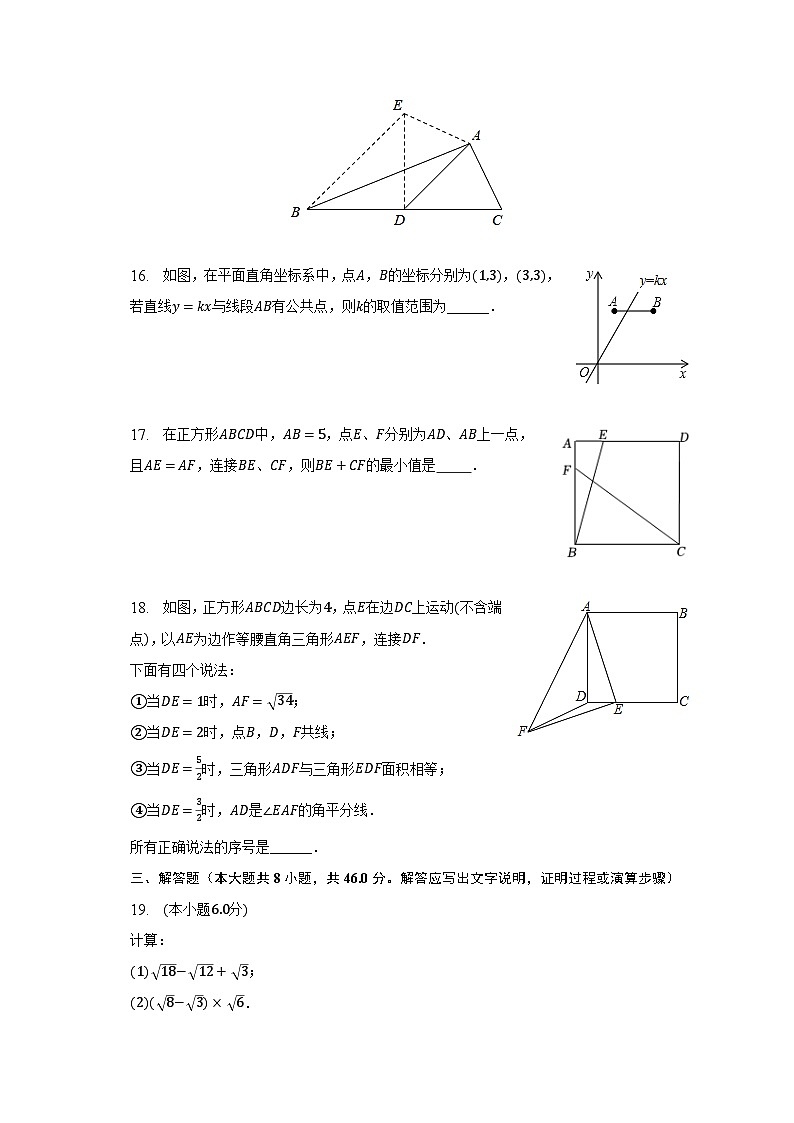
15. 如图，AD是△ABC的中线，∠ADC=45°，BC=4cm，把△ACD沿AD翻折，使点C落在E的位置，则BE为______ ．

16. 如图，在平面直角坐标系中，点A，B的坐标分别为(1,3)，(3,3)，若直线y=kx与线段AB有公共点，则k的取值范围为______．


17. 在正方形ABCD中，AB=5，点E、F分别为AD、AB上一点，且AE=AF，连接BE、CF，则BE+CF的最小值是          ．


18. 如图，正方形ABCD边长为4，点E在边DC上运动(不含端点)，以AE为边作等腰直角三角形AEF，连接DF．
下面有四个说法：
①当DE=1时，AF= 34；
②当DE=2时，点B，D，F共线；
③当DE=52时，三角形ADF与三角形EDF面积相等；
④当DE=32时，AD是∠EAF的角平分线．
所有正确说法的序号是______．
三、解答题（本大题共8小题，共46.0分。解答应写出文字说明，证明过程或演算步骤）
19. (本小题6.0分)
计算：
(1) 18− 12+ 3；
(2)( 8− 3)× 6．
20. (本小题5.0分)
已知一次函数y=kx+b，当x=1时，y的值为−1，当x=−1时，y的值为−5．
(1)求一次函数y=kx+b的解析式；
(2)将一次函数y=kx+b的图象向上平移2个单位长度，求所得到新的函数图象与x轴、y轴的交点坐标．
21. (本小题5.0分)
如图，矩形纸片ABCD中，AB=8，AD=6，折叠纸片使AD边落在对角线BD上，点A落在点A′处，折痕为DG，求AG的长．

22. (本小题5.0分)
如图，在▱ABCD中，过点A作AE⊥BC于点E，AF⊥DC于点F，且BE=DF．
(1)求证：▱ABCD是菱形；
(2)若∠EAF=60°，CF=2，求菱形ABCD的面积．

23. (本小题6.0分)
已知，如图，在△ABC中，AB=AC，AD是BC边的中线，过点A作BC的平行线，过点B作AD的平行线，两线交于点E，连接DE交AB于点O．
(1)求证：四边形ADBE是矩形；
(2)若BC=8，AO=52，求四边形AEBC的面积．


24. (本小题6.0分)
如图，在平面直角坐标系中，一次函数y=−12x+m的图象l1分别与x，y轴交于A，B两点，正比例函数的图象l2与l1交于点C(2,4)．
(1)求m的值及l2的解析式；
(2)若点M是直线y=−12x+m上的一个动点，连接OM，当△AOM的面积是△BOC面积的2倍时，请求出符合条件的点M的坐标；
(3)一次函数y=kx+2的图象为l3，且l1，l2，l3不能围成三角形，直接写出k的值．

25. (本小题6.0分)
如图，在正方形ABCD中，E是边AB上的一动点，点F在边BC的延长线上，且CF=AE，连接DE、DF．

(1)求证：DE⊥DF；
(2)连接EF，取EF中点G，连接DG并延长交BC于H，连接BG．
①依题意，补全图形；
②求证：BG=DG；
③若∠EGB=45°，用等式表示线段BG、HG与AE之间的数量关系，并证明．
26. (本小题7.0分)
对于实数x，[x]表示不小于x的最小整数，例如：[1]=1，[2.5]=3，点P(x,y)为第一象限中的点，将点P分别向上，向下平移[y]个单位得到点P1，P3；将点P分别向左，向右平移[x]个单位得到点P2，P4，我们称菱形P1P2P3P4叫做点P的“伴随菱形”.例如：点(3,32)的伴随菱形是以点(3,72)，(0,32)，(3,−12)，(6,32)构成的菱形．
(1)在图中画出点A(32,1)的伴随菱形，该菱形的面积为______；
(2)若点B(t,1)的伴随菱形与点A(32,1)的伴随菱形恰有3个公共点，求满足条件的t的最小值；
(3)若点C(32,2)与点D(m,n)所对应的伴随菱形面积相同，且点D(m,n)在函数y=kx的图象上，直接写出k的取值范围．


答案和解析

1.【答案】C 
【解析】解：A：2 12，被开方数含有分母，所以A选项不是最简二次根式，不符合题意；
B： 4=2，所以B选项不是最简二次根式，不符合题意；
C： 10，所以C选项是最简二次根式，符合题意；
D： 12=2 3，所以D选项不是最简二次根式，不符合题意；
故选：C．
根据最简二次根式的条件：(1)被开方数不含分母；(2)被开方数中不含能开得尽方的因数或因式逐项进行判定即可得出答案．
本题主要考查最简二次根式，熟知最简二次根式的定义是解题的关键．

2.【答案】A 
【解析】解：A.3与2 2不能合并，所以A选项符合题意；
B. 8÷2=2 2÷2= 2，所以B选项不符合题意；
C. 2× 3= 2×3= 6，所以C选项不符合题意；
D. 8− 2=2 2− 2= 2，所以D选项不符合题意．
故选：A．
根据二次根式的加法运算对A选项进行判断；根据二次根式的性质对B选项进行判断；根据二次根式的乘法法则对C选项进行判断；根据二次根式的减法运算对D选项进行判断．
本题考查了二次根式的混合运算：熟练掌握二次根式的性质、二次根式的乘法法则、除法法则是解决问题的关键．

3.【答案】A 
【解析】解：在Rt△ABC中，∠ACB=90°，AB=5，AC=4，
由勾股定理得：BC= AB2−AC2= 52−42=3，
∴BC的长为3．
故选：A．
在Rt△ABC中，已知AB与AC的长，利用勾股定理求出BC的长即可．
本题考查了勾股定理，能灵活运用定理进行计算是解题的关键．

4.【答案】A 
【解析】解：∵k=−2−2，
∴y10，y随x的增大而增大；若k0，d>0，
∴ac1时，ax+b−1，c>0，
∴c>d，故⑤正确，
故选：D．
根据函数的图象以及一次函数的性质判断即可．
本题考查了一次函数与一元一次不等式，一次函数的性质，熟练掌握一次函数图象与系数的关系是解题的关键．难度适中．

10.【答案】D 
【解析】解：在Rt△AOB中，OB=1，AB= 10，∠AOB=90°，
∴OA= AB2−OB2=3．
∵四边形ABCD为菱形，且对角线BD与x轴平行，
∴点D的坐标为(6,1)．
当y=1时，x+3=1，
解得：x=−2．
∵将菱形ABCD沿x轴向左平移m个单位，点D落在△EOF的内部(不包括三角形的边)，
∴6