





初中数学人教版九年级上册23.2.3 关于原点对称的点的坐标教学ppt课件
展开1. 掌握两点关于原点对称时,横纵坐标的关系.2. 会在平面直角坐标系内作关于原点对称的图形.3. 进一步体会数形结合的思想.
关于原点对称的点的坐标关系.
应用关于原点对称的点的坐标的关系作图.
1.下列各点分别在坐标平面的什么位置上?
A(3,2)B(0,-2)C(-3,-2)D(-3,0)E(-1.5,3.5)F(2,-3)
A(-3,- 2 )
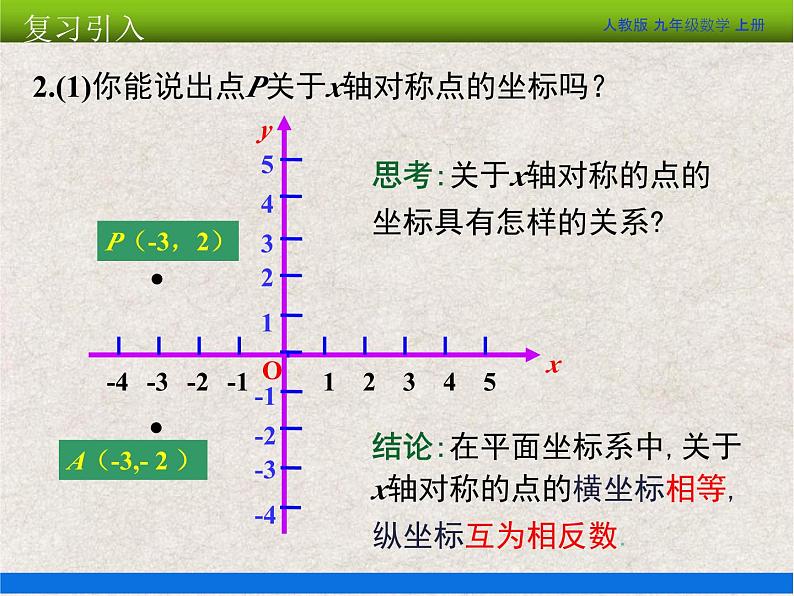
2.(1)你能说出点P关于x轴对称点的坐标吗?
思考:关于x轴对称的点的坐标具有怎样的关系?
结论:在平面坐标系中,关于x轴对称的点的横坐标相等,纵坐标互为相反数.
(2)你能说出点P关于y轴对称点的坐标吗?
思考:关于y轴对称的点的坐标具有怎样的关系?
结论:在直角坐标系中,关于y轴对称的点的纵坐标相等,横坐标互为相反数
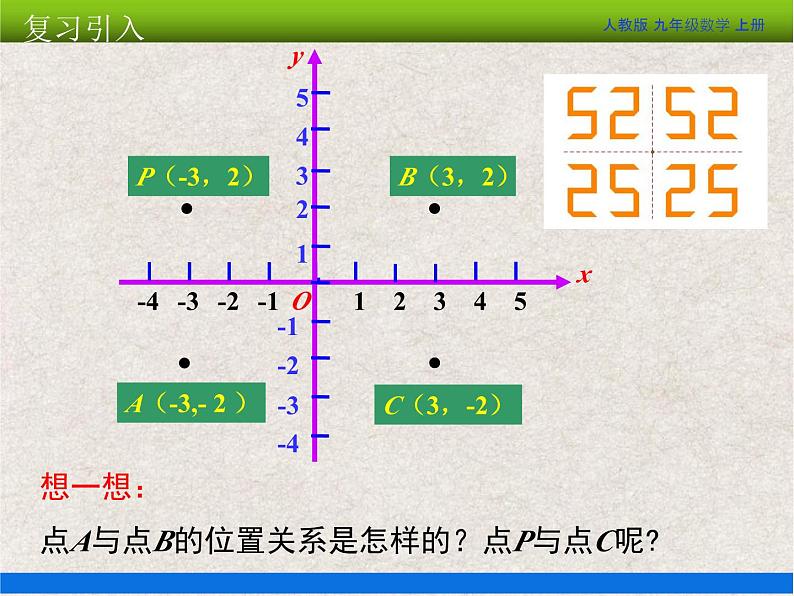
想一想:点A与点B的位置关系是怎样的?点P与点C呢?
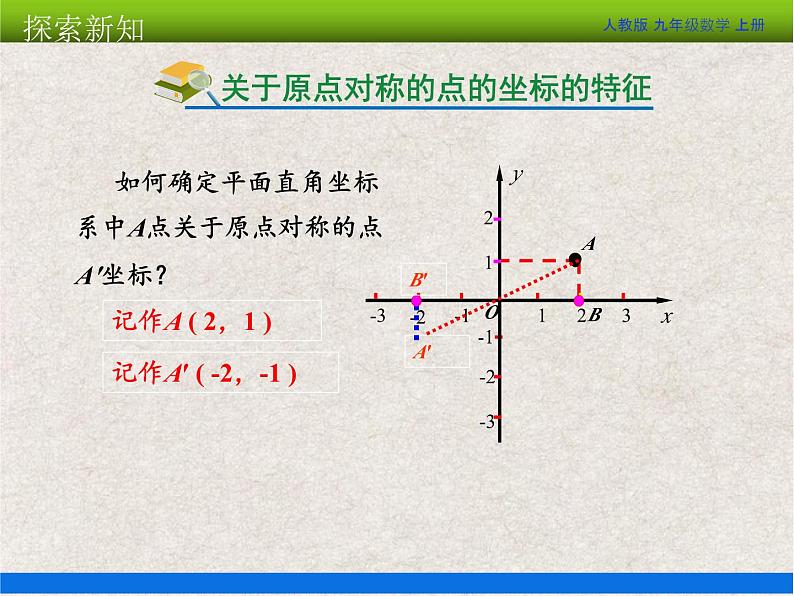
如何确定平面直角坐标系中A点关于原点对称的点A′坐标?
记作A′ ( -2,-1 )
记作A ( 2,1 )
关于原点对称的点的坐标的特征
★关于原点对称的点的坐标规律
第一象限内的点关于原点的对称点在第三象限,第二象限内的点关于原点的对称点在第四象限,坐标轴上的点关于原点的对称点仍在坐标轴上.
横坐标、纵坐标的符号都互为相反数
点P(a,b)关于原点对称的点的坐标为P′(-a,-b); 点P(a,b)关于 x 轴对称的点的坐标为P′(a,-b); 点P(a,b)关于 y 轴对称的点的坐标为P′(-a, b).
简记为:“关于谁,谁不变,关于原点都改变”.
-4 -3 -2 -1 1 2 3 4
例 在直角坐标系中,作出下列点关于原点的对称点,并写出它们的坐标.
A(4,0) B(0,-3) C(2,1) D(-1,2) E(-3,-2)
2.已知点P(2a+b,-3a)与点P'(8,b+2).若点P与点P'关于x轴对称,则a=_____ b=_______.若点P与点P'关于y轴对称,则a=_____ b=_______.若点P与点P'关于原点对称,则a=_____ b=_______.
①下列各点中哪两个点关于原点O对称?A(-5,0),B(0,2),C(2,-1),D(2,0),E(0,5),F(-2,1),G(-2,-1).
解:C、F关于原点O对称.
②已知点A(m-1,2),B(-3,n+1)两点关于原点对称,则m=____,n=_____.
例 若点A(2m-1,2m+3)与B(-2-n,1-8n)关于原点O对称, 求(m- n)2020的值.
例 如图,利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.
解:△ABC的三个顶点 A(-4,1),B(-1, -1),C(-3,2)
A′(4,-1),B′(1,1),C′(3,-2)
关于原点的对称点分别为
依次连接A ′B ′ ,B ′ C ′ ,C ′ A ′ ,就可得到与△ABC关于原点对称的△ A′B′ C ′ .
利用关于原点对称的点的坐标关系作图
作关于原点对称的图形的步骤:(1)写出各点关于原点对称的点的坐标;(2)在坐标平面内描出这些对称点;(3)参照原图形顺次连接各点,即为所求作的对称图形.
例 如图,利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.
分析:要作出线段AB关于原点的对称线段,只要作出点A、点B关于原点的对称点A′、B′即可.
例 如图,作出与△ABC关于原点对称的图形.
解:点A(-4,1) 、B(-3,2) 、C(-1,-1)关于原点对称的点的坐标分别是A′(4,-1),B′(3,-2),C′(1,1).
1.写出下列各点关于原点的对称点的坐标. A(3,1) B(-2,3) C(-1,-2) D(2,-3)
A(-3,-1) B(2,-3) C(1,2) D(-2,3)
2.若点A(m,-2),B(1,n)关于原点对称,则 m=_____,n=_____ .
3.已知点M(1-2m,m-1)关于原点的对称点在第一象限,则m的取值范围在数轴上表示正确的是( )
4.在如图所示编号为①、②、③、④的四个三角形中,关于y轴对称的两个三角形的编号为 ;关于坐标原点O对称的两个三角形的编号为________.
5.在平面直角坐标系中,已知A(2,3),B(0,1),C(3,1),若线段AC与BD互相平分,则点D关于坐标原点的对称点的坐标为 .
6.如图,阴影部分组成的图案 ,既是关于x轴成轴对称的图形又是关于坐标原点O 成中心对称的图形.若点A的坐标是(1,3),则点M 和点N 的坐标分别是:
7.如图,已知A的坐标为( ,2),点B的坐标为(-1, ),菱形ABCD的对角线交于坐标原点O.求C,D两点的坐标.
8.如图,△DEF是由△ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;(2)若点P(a+3,4-b)与点Q(2a,2b-3)也是通过上述变换得到的对应点,求a、b的值.
解:(1)A(2,3),D(-2,-3),B(1,2),E(-1,-2),C(3,1), F(-3,-1),对应点的坐标关于原点对称. (2)∵点P(a+3,4-b)与点Q(2a,2b-3)关于原点对称. ∴a+3=-2a,4-b=3-2b. ∴a=-1,b=-1.
拓展提升试写出直线y=3x-5关于原点对称的直线的函数解析式.
答案是:y= 3x+5
关于原点对称的点的坐标
P(x,y)关于原点的对称点为P'(-x,-y).
作出关于原点对称的图形,先求出对称点的坐标再描点画图.
人教版九年级上册23.2.3 关于原点对称的点的坐标教案配套ppt课件: 这是一份人教版九年级上册23.2.3 关于原点对称的点的坐标教案配套ppt课件,共21页。PPT课件主要包含了学习目标,-2-2,1-3,2-2,归纳总结,-30-5,∵a为整数,∴a012等内容,欢迎下载使用。
初中人教版第二十三章 旋转23.2 中心对称23.2.3 关于原点对称的点的坐标课文内容ppt课件: 这是一份初中人教版第二十三章 旋转23.2 中心对称23.2.3 关于原点对称的点的坐标课文内容ppt课件,共24页。PPT课件主要包含了-x-y,互为相反数,都互为相反数,-3-5,-35等内容,欢迎下载使用。
数学九年级上册23.2.3 关于原点对称的点的坐标习题ppt课件: 这是一份数学九年级上册23.2.3 关于原点对称的点的坐标习题ppt课件,共14页。PPT课件主要包含了-x-y,关于y轴对称,关于x轴对称,关于原点对称,-58,-32等内容,欢迎下载使用。














