北师大版七年级上册5.6 应用一元一次方程——追赶小明优质课教案设计

这是一份北师大版七年级上册5.6 应用一元一次方程——追赶小明优质课教案设计，共6页。教案主要包含了总结归纳等内容，欢迎下载使用。
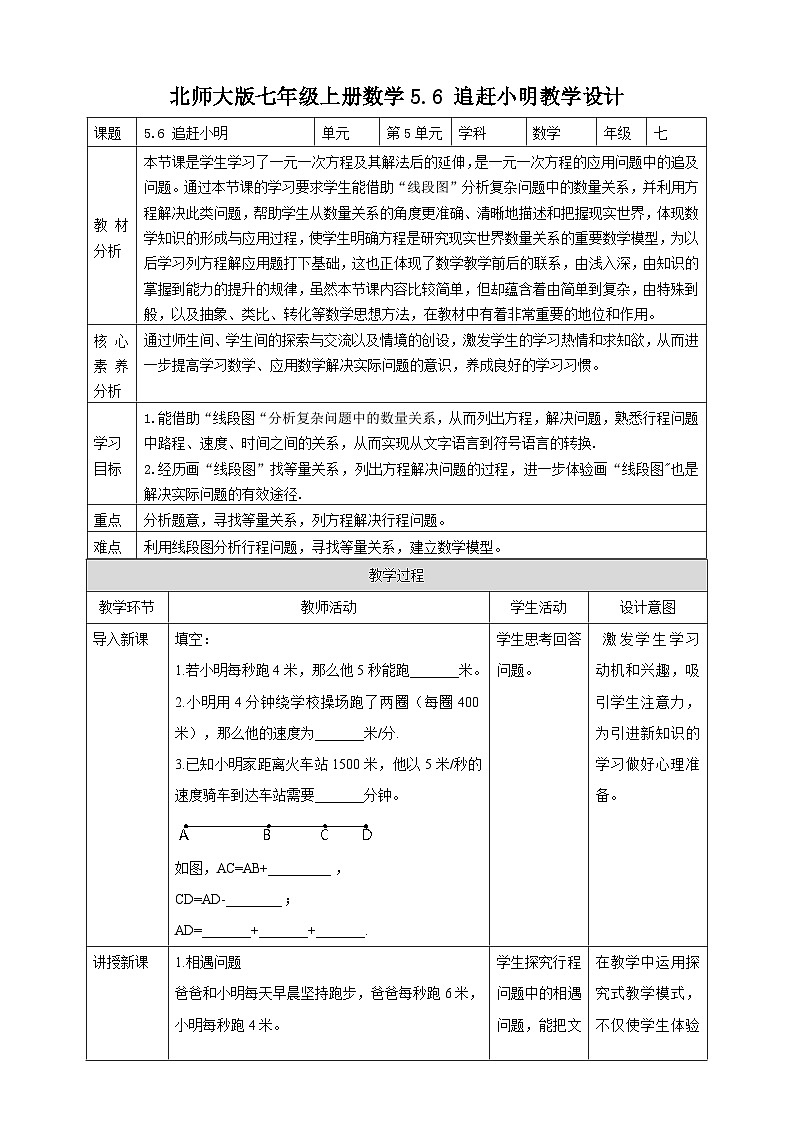
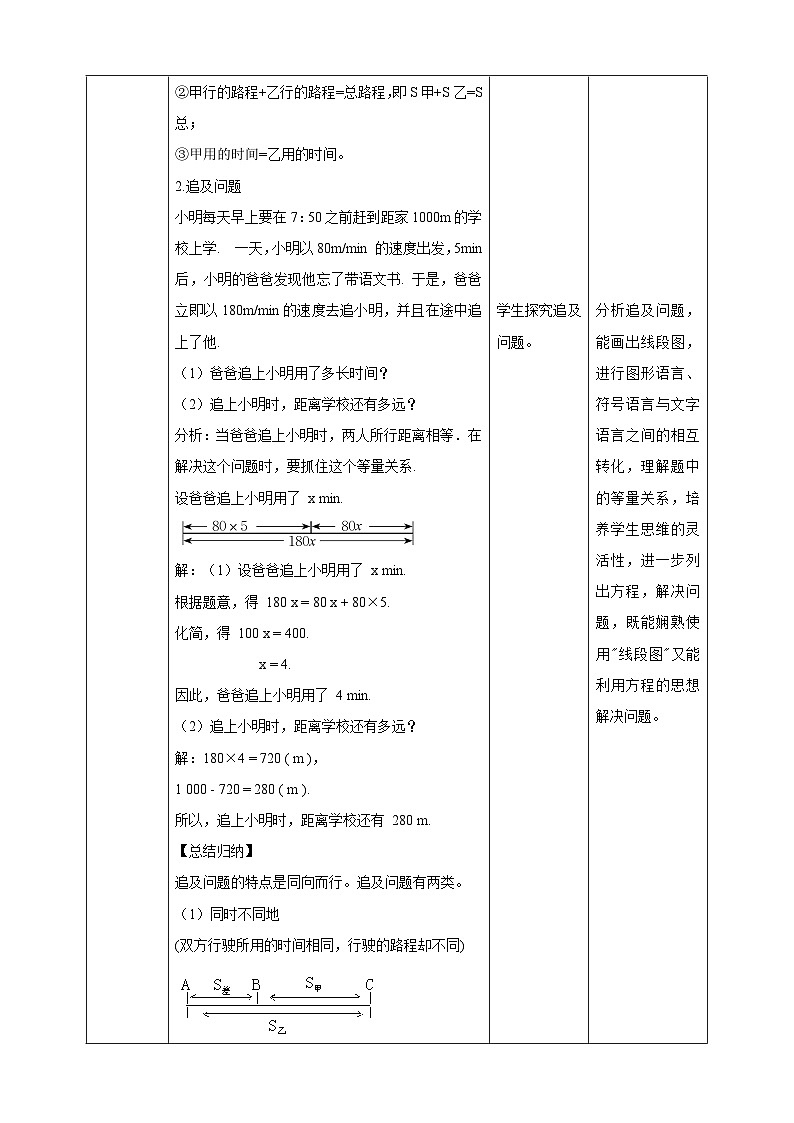
北师大版七年级上册数学5.6 追赶小明教学设计课题 5.6 追赶小明单元第5单元学科数学年级七教材分析本节课是学生学习了一元一次方程及其解法后的延伸，是一元一次方程的应用问题中的追及问题。通过本节课的学习要求学生能借助“线段图”分析复杂问题中的数量关系，并利用方程解决此类问题，帮助学生从数量关系的角度更准确、清晰地描述和把握现实世界，体现数学知识的形成与应用过程，使学生明确方程是研究现实世界数量关系的重要数学模型，为以后学习列方程解应用题打下基础，这也正体现了数学教学前后的联系，由浅入深，由知识的掌握到能力的提升的规律，虽然本节课内容比较简单，但却蕴含着由简单到复杂，由特殊到般，以及抽象、类比、转化等数学思想方法，在教材中有着非常重要的地位和作用。核心素养分析通过师生间、学生间的探索与交流以及情境的创设，激发学生的学习热情和求知欲，从而进一步提高学习数学、应用数学解决实际问题的意识，养成良好的学习习惯。学习目标1.能借助“线段图“分析复杂问题中的数量关系，从而列出方程，解决问题，熟悉行程问题中路程、速度、时间之间的关系，从而实现从文字语言到符号语言的转换.2.经历画“线段图”找等量关系，列出方程解决问题的过程，进一步体验画“线段图"也是解决实际问题的有效途径. 重点分析题意，寻找等量关系，列方程解决行程问题。难点利用线段图分析行程问题，寻找等量关系，建立数学模型。 教学过程教学环节教师活动学生活动设计意图导入新课填空：1.若小明每秒跑4米，那么他5秒能跑_______米。2.小明用4分钟绕学校操场跑了两圈（每圈400米），那么他的速度为_______米/分.3.已知小明家距离火车站1500米，他以5米/秒的速度骑车到达车站需要_______分钟。如图，AC=AB+_________，CD=AD-________；AD=_______+_______+_______.学生思考回答问题。 激发学生学习动机和兴趣，吸引学生注意力，为引进新知识的学习做好心理准备。讲授新课1.相遇问题爸爸和小明每天早晨坚持跑步，爸爸每秒跑6米，小明每秒跑4米。如果他们站在百米跑道的两端同时相向起跑，那么几秒后两人相遇？你能画出线段图吗？等量关系：爸爸的路程+小明的路程=100米解：设x秒后爸爸和小明相遇。根据题意：4x+6x=100            10x=100              x=10答：爸爸和小明10秒后相遇。在审题过程中，如果能把文字语言变成图形语言——线段图，即可使问题更加直观，等量关系更加清晰. 我们只要设出未知数，并用代数式表示出来，便可以得到方程.【总结归纳】相遇问题是比较重要的行程问题，其特点是相向而行。如图（1）就是相遇问题，图（2）也可看成相遇问题来解决。相遇问题中的相等关系：①甲、乙的速度和×相遇时间=总路程；②甲行的路程+乙行的路程=总路程，即S甲+S乙=S总；③甲用的时间=乙用的时间。2.追及问题小明每天早上要在7：50之前赶到距家1000m的学校上学.  一天，小明以80m/min 的速度出发，5min后，小明的爸爸发现他忘了带语文书. 于是，爸爸立即以180m/min的速度去追小明，并且在途中追上了他.（1）爸爸追上小明用了多长时间？（2）追上小明时，距离学校还有多远？分析：当爸爸追上小明时，两人所行距离相等．在解决这个问题时，要抓住这个等量关系.设爸爸追上小明用了 x min.解：（1）设爸爸追上小明用了 x min.根据题意，得 180 x = 80 x + 80×5.化简，得 100 x = 400.            x = 4.因此，爸爸追上小明用了 4 min.（2）追上小明时，距离学校还有多远？解：180×4 = 720 ( m )，1 000 - 720 = 280 ( m ).所以，追上小明时，距离学校还有 280 m.【总结归纳】追及问题的特点是同向而行。追及问题有两类。（1）同时不同地(双方行驶所用的时间相同，行驶的路程却不同)等量关系：乙的行程-甲的行程=行程差；即S乙-S甲=S差。速度差×追及时间=追及距离。甲用的时间=乙用的时间。（2）同地不同时(由于行驶双方出发时间有先后，故行驶过程中用用的时间不同，双方出发地相同，故行驶的路程相同，)等量关系：甲的行程=乙的行程；即S甲=S乙。议一议育红学校七年级学生步行到郊外旅行．七（1）班的学生组成前队，步行速度为4km/h，七（2）班的学生组成后队，速度为6km/h．前队出发1h后，后队才出发，同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络，他骑车的速度为12km/h.【思考】后队用多长时间追上前队？等量关系：前队走的路程=后队走的路程.解：设后队出发x小时追上前队，根据题意，得 6 x = 4 × 1+ 4 x.化简，得 2 x = 4.                 x = 2.所以后队2小时可追上前队.【思考】后队出发到追上前队时，联络员骑行了多少千米？解：联络员的骑行速度为12千米/时，后队追上前队的时间是2小时，所以联络员骑行的距离是12×2=24（千米）.学生探究行程问题中的相遇问题，能把文字语言变成图形语言——线段图。               学生总结相遇问题的线段图和相等关系。                 学生探究追及问题。                                                        在教学中运用探究式教学模式，不仅使学生体验教学再创造的思维过程，而且还培养了学生的创造意识和科学精神。             对概念的分析和归纳,培养学生的口头表达能力和语言组织能力,同时渗透类比思想.              分析追及问题，能画出线段图，进行图形语言、符号语言与文字语言之间的相互转化，理解题中的等量关系，培养学生思维的灵活性，进一步列出方程，解决问题，既能娴熟使用"线段图"又能利用方程的思想解决问题。课堂练习1.A，B 两地相距280 m，甲、乙两人同时相向而行，甲从A 地每秒跑8 m，乙从B 地每秒跑6m，那么几秒后甲、乙两人相遇？分析：等量关系是：甲所用时间=乙所用时间，甲跑过的路程+ 乙跑过的路程=A，B 两地之间的距离.解：设x s 后甲、乙两人相遇.根据题意, 得8x+6x =280，解得x=20.答：20 s 后甲、乙两人相遇.2.甲、乙两车站相距450 km，一列慢车从甲站开出，每小时行驶65 km，—列快车从乙站开出，每小时行驶85 km.两车同时开出， 相向而行，那么两车行驶多少小时相遇？解：设两车行驶x h相遇．根据题意，得65x＋85x＝450，解得x＝3.因此，两车行驶3 h相遇．3.李成在王亮的前方10 米处，若李成每秒跑7 米，王亮每秒跑7.5 米，两人同时起跑，问：王亮跑多少米可以追上李成？解：设x 秒后王亮追上李成. 根据题意，得7.5x－7x=10.解得x=20.7.5×20=150(米).答：王亮跑150 米可以追上李成.4.一架飞机在A，B两城市之间飞行，风速为20 km/h，顺风飞行需要8 h，逆风飞行需要8.5 h．求无风时飞机的飞行速度和A，B两城市之间的航程．解：设无风时飞机的飞行速度为x km/h.根据题意，得8(x＋20)＝8.5(x－20)，解得x＝660.所以8(x＋20)＝8×(660＋20)＝5 440.答：无风时飞机的飞行速度为660 km/h，A，B两城市之间的航程为5 440 km.学生做练习，教师订正答案。通过练习来巩固、强化课堂上所学的知识，并且培养学生综合运用所学的知识和技能解决问题的能力，培养学生的应用意识。课堂小结本节课你学到了什么？1.相遇问题2.追及问题3.解决行程问题的基本步骤：①问题的已知条件；②画出线段图；③找出等量关系；④列方程并求解；⑤检验；⑥作答。学生总结归纳。充分发挥学生的主体作用，有助于学生在理解新知识的基础上，及时把知识系统化，条理化。板书课题：5.6  追赶小明一、相遇问题二、追及问题三、解决行程问题的基本步骤