【同步讲义】（人教A版2019）高一数学必修一：《第三章 函数的概念与性质》学业水平质量检测（A卷）

《第三章  函数概念与性质》学业水平质量检测（A卷）

学校:___________姓名：___________班级：___________考号：___________

一．选择题

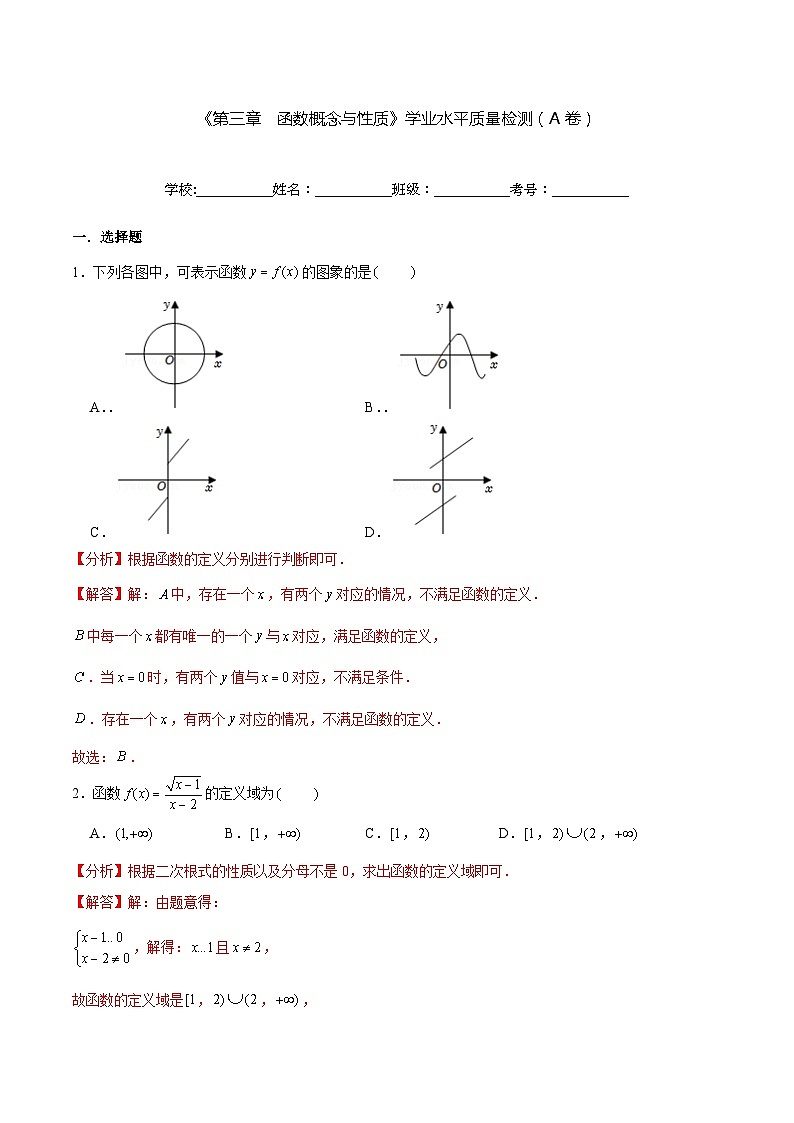
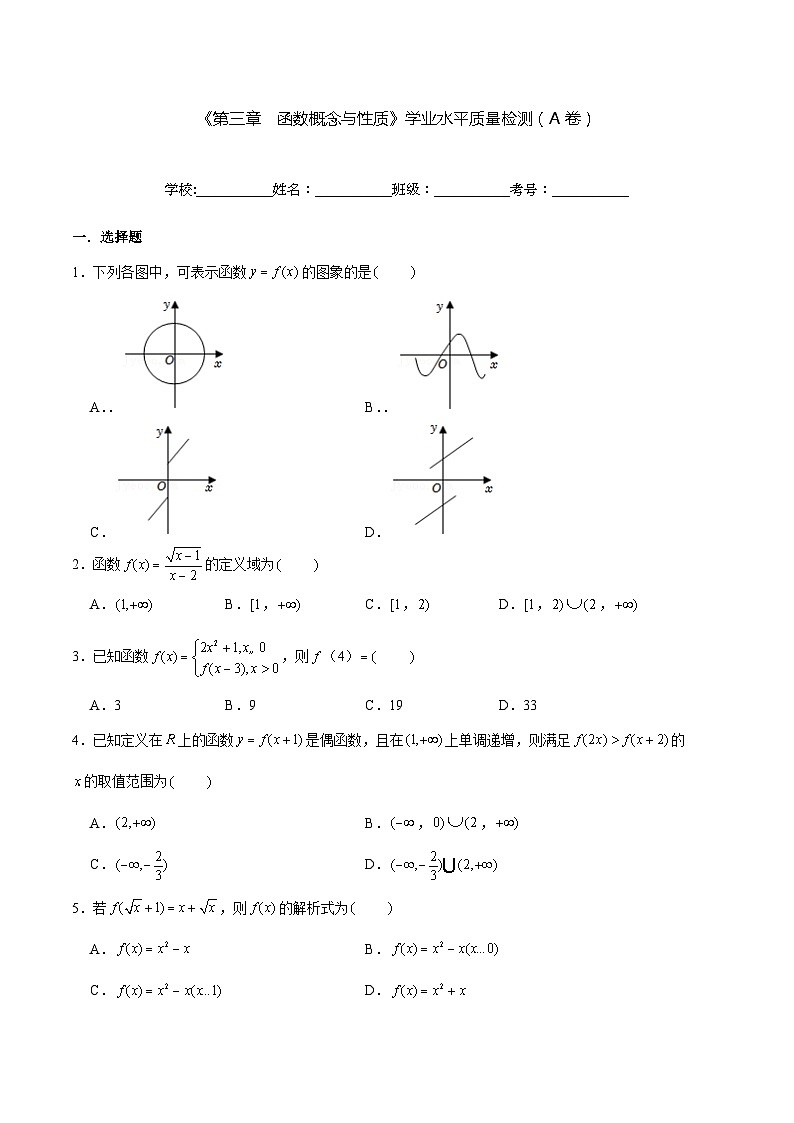
1．下列各图中，可表示函数的图象的是　　

A．． B．． 

C． D．

【分析】根据函数的定义分别进行判断即可．

【解答】解：中，存在一个，有两个对应的情况，不满足函数的定义．

中每一个都有唯一的一个与对应，满足函数的定义，

．当时，有两个值与对应，不满足条件．

．存在一个，有两个对应的情况，不满足函数的定义．

故选：．

2．函数的定义域为　　

A． B．， C．， D．，，

【分析】根据二次根式的性质以及分母不是0，求出函数的定义域即可．

【解答】解：由题意得：

，解得：且，

故函数的定义域是，，，

故选：．

3．已知函数，则（4）　　

A．3 B．9 C．19 D．33

【分析】根据题意，由函数的解析式可得（4）（1），进而计算可得答案．

【解答】解：根据题意，函数，

则（4）（1）；

故选：．

4．已知定义在上的函数是偶函数，且在上单调递增，则满足的

的取值范围为　　

A． B．，， 

C． D．

【分析】根据题意，函数的图象关于直线对称，再代入求范围即可．

【解答】解：由题意知，函数的图象关于直线对称，且在上单调递增，又，所以，平方并化简，得，解得或．

故选：．

5．若，则的解析式为　　

A． B． 

C． D．

【分析】根据题意设，则，求出，即可得出的解析式．

【解答】解：函数，

设，则，

，

，

，．

故选：．

6．函数对任意，都有，的图形关于对称，且（7），则　　

A． B．1 C．0 D．2

【分析】根据题意，分析函数的奇偶性和周期性，由此可得（7），即可得答案．

【解答】解：根据题意，函数对任意，都有，则函数的周期为，

又的图形关于对称，则的图象关于点对称，

故为上的奇函数，

（7）；

故选：．

7．已知函数在上是单调的函数，则的取值范围是　　

A．， B．， C． D．，

【分析】由一次函数、二次函数的性质，得不等式，解出即可．

【解答】解：函数在上是单调的函数，

函数是上的增函数，

，解得：，

时，，解得：，

综上的取值范围是：，．

故选：．

8．已知是定义在上的奇函数，且当时，，对任意的，，不等式恒成立，那么实数的取值范围是　　

A．， B．， C．， D．，

【分析】由当时，，函数是奇函数，可得当时，，从而在上是单调递增函数，且满足，再根据不等式在，恒成立，可得在，恒成立，即可得出答案．

【解答】解：是定义在上的奇函数，且当时，

当，有，，

，即，

，

在上是单调递增函数，

且满足，

不等式在，恒成立，

在，恒成立，

解得在，恒成立，

解得：，则实数的取值范围是：，，

故选：．

二．多选题

9．函数在下列区间　　上单调递减

A． B． C．， D．

【分析】结合函数的图象，求出函数的递减区间即可．

【解答】解：画出函数的图象，如图示：

，

显然在递减，在递增，在递减，在递增，

故选：．

10．下列各组函数是同一函数的是　　

A．与 

B．与 

C．与 

D．与

【分析】根据两个函数的定义域相同，对应关系也相同，即可判断它们是同一函数．

【解答】解：对于，的定义域为，的定义域为，定义域相同，对应关系也相同，是同一函数；

对于，的定义域为，的定义域为，对应关系不同，不是同一函数；

对于，的定义域为，的定义域为，定义域相同，对应关系也相同，是同一函数；

对于，的定义域为，的定义域为，对应关系不同，不是同一函数．

故选：．

11．给出下列命题，其中是错误命题的是　　

A．若函数的定义域为，，则函数的定义域为， 

B．函数的单调递减区间是，， 

C．若定义在上的函数在区间，上是单调增函数，在区间上也是单调增函数，则在上是单调增函数 

D．，是定义域内的任意的两个值，且，若，则是减函数

【分析】直接利用函数的性质的应用，函数的定义域，函数的单调性的应用求出结果．

【解答】解：①若函数的定义域为，，则函数的定义域为：

令，解得．故函数的定义域为，．故选项错误．

②函数的单调递减区间是和，故选项错误．

③如下图，

函数在区间，上是单调增函数，在区间上也是单调增函数，但是函数在上不是单调函数．故错误．

④，是定义域内的任意的两个值，且，若，即，所以函数是减函数．故正确．

故选：．

12．已知函数对任意都有（2），若的图象关于直线对称，且对任意的，，且，都有，则下列结论正确的是　　

A．是偶函数 B．的周期 

C． D．在单调递减

【分析】根据图象的平移变换规律，奇偶函数的性质、周期的定义、单调性的定义，结合已知条件对每个选项进行判断．

【解答】解：因为的图象关于直线对称，所以将的图象向左平移一个单位，得的图象，关于轴对称，故是偶函数，故正确；

则再令“任意都有（2），”中的，可得（2）（2），故（2），所以（2），故对任意的恒成立，故的周期为，故正确；

所以（2），故正确；

因为任意的，，且，都有，故在上是单调增函数，根据周期为4，故该函数在上也是增函数，故错误．

故选：．

三．填空题

13．若幂函数的图象经过点，，则的值是 　　．

【分析】根据幂函数的定义，利用待定系数法求出函数的解析式，然后代入求值即可．

【解答】解：设幂函数为，

的图象经过点，，

（8），

即，

则，则，

则，

则，

故答案为：

14．设函数，若恒成立，则实数的值为　　．

【分析】由的解析式，求得的解析式，结合恒等式的性质，可得的方程，解方程可得的值．

【解答】解：函数，

若，

即为，

由恒等式的性质可得，且，

解得，

故答案为：．

15．设，若是的最小值，则的取值范围为 　，　．

【分析】分别由，，综合得出的取值范围．

【解答】解：当时，，

由题意得：，

又，

，

故答案为：，．

16．已知奇函数的定义域为且在上连续．当时，不等式的解集为，则当时，的解集为　，，，，　．

【分析】由已知可得当时，不等式的解集，根据函数的奇偶性可将当时，的解集为，令，可得的解集，从而可得结论．

【解答】解：当时，不等式的解集为，

不等式的解集为，，，，

是定义域为的奇函数，，

当时，的解集为，

令，则的解集为，

的解集为，，，，，

故答案为：，，，，，

四．解答题

17．已知，求的解析式和定义域．

【分析】利用换元法设，进行求解即可．

【解答】解：设，则，

则，

则，

即，

即，函数的定义域为．

18．已知二次函数的最小值为1，且（2）．

（1）求函数的解析式；

（2）求在上的最大值；

（3）若函数在区间，上不单调，求实数的取值范围．

【分析】（1）由题意知二次函数的对称轴为，从而设函数，代入求解即可；

（2）根据二次函数的性质求最大值即可；

（3）由题意知对称轴在区间上，从而求得．

【解答】解：（1）（2），

二次函数的对称轴为，

设函数，

则，

解得；

故；

（2），

，

即在上的最大值为；

（3）函数在区间，上不单调，

，

解得，；

故实数的取值范围为．

19．某公司生产一种电子仪器的固定成本为20000元，每生产一台仪器需增加投入100元，已知总收益（单位：元）满足其中（单位：台）是仪器的月产量．

（1）将利润表示为月产量的函数；

（2）当月产量为何值时，公司利润最大？最大为多少元？（总收益总成本利润）

【分析】（1）利润收益成本，由已知分两段当时，和当时，求出利润函数的解析式；

（2）分段求最大值，两者大者为所求利润最大值．

【解答】解：（1）由于月产量为台，则总成本为，

从而利润；

（2）当时，，

所以当时，有最大值25000；

当时，是减函数，

所以．

所以当时，有最大值25000，

即当月产量为300台时，公司所获利润最大，最大利润是25000元．

20．已知函数．

（1）若，求的定义域；

（2）若在区间，上是减函数，求实数的取值范围．

【分析】（1）函数定义域的常规求法，被开方数为非负数即可；

（2）利用一次函数的单调性，列出不等式求解即可．

【解答】解：（1）由得，

当时，解得，此时的定义域为，；

当时，解得，此时的定义域为，．

（2）；

在区间，上是减函数，

即 解得．

21．已知函数．

（1）若函数的最大值为0，求实数的值；

（2）若函数在，上单调递减，求实数的取值范围；

（3）是否存在实数，使得在，上的值域恰好是，？若存在，求出实数的值；若不存在，说明理由．

【分析】（1）由的最大值为0，即二次函数有且只有一个值0，可得△，从而求出的取值．

（2）由图象的性质得，在对称轴右侧时单调递减，从而得出的取值范围．

（3）讨论的对称轴在，的左侧、右侧以及在，上时三种情况，从而求出满足条件的的值．

【解答】解：（1）函数，最大值为0，

且二次函数的图象是开口向下的抛物线，

有且只有一个值0，

即△，

的值为0或4．

（2）函数图象是开口向下的抛物线，对称轴是；

要使在，上是单调递减的，应满足，；

的取值范围是．

（3）对的对称轴在，的左侧、右侧以及在，上时的三种情况进行讨论：

①当，即时，在，上是减函数，

若存在实数，使在，上的值域是，，

则有，即，

解得不存在；

②当，即时，在，上是增函数，

则有，即，

解得；

③当，即时，在，上先增后减，

所以在处取最大值；

，

解得或6（均不满足条件，舍去）；

综上，存在实数，使在，上的值域恰好是，．

22．已知函数是定义在区间，上的奇函数，且，若对于任意的，，有．

（1）判断函数的单调性（不要求证明）；

（2）解不等式；

（3）若，存在，，对于任意的，，不等式恒成立，求实数的取值范围．

【分析】（1）由对于任意的，，有即可判断；

（2）结合（1）的单调性及奇函数的条件即可求解不等式．

（3）结合已知不等式可转化为求解最值，进行变换主元构造一次函数，结合一次函数的单调性可求．

【解答】解（1）函数在区间，上是减函数．

（2）由（1）知函数在区间，上是减函数，

由，

解得．

所以不等式的解集为．

（3）因为函数在区间，上是减函数，且，

若，存在，，对于任意的，，不等式恒成立，

只需对任意的，，恒成立．

令，此时可以看作的一次函数，且在，时，恒成立．

因此只需，

解得，

所以实数的取值范围为，．