【同步讲义】（人教A版2019）高中数学选修第三册：拓展一：条件概率、全概率公式及贝叶斯公式8种常见考法归类 讲义

这是一份【同步讲义】（人教A版2019）高中数学选修第三册：拓展一：条件概率、全概率公式及贝叶斯公式8种常见考法归类 讲义，文件包含同步讲义人教A版2019高中数学选修第三册拓展一条件概率全概率公式及贝叶斯公式8种常见考法归类原卷版docx、同步讲义人教A版2019高中数学选修第三册拓展一条件概率全概率公式及贝叶斯公式8种常见考法归类解析版docx等2份试卷配套教学资源，其中试卷共52页， 欢迎下载使用。
 拓展一：条件概率、全概率公式及贝叶斯公式
8种常见考法归类

考点一 条件概率的定义及计算
（一）利用定义求条件概率
（二）缩小样本空间求条件概率
考点二 包含事件的条件概率问题
考点三 相互独立事件的条件概率问题
考点四 概率的乘法公式
考点五 条件概率的性质及应用
考点六 全概率公式的计算
考点七 全概率公式解决实际问题
（一）产品质检
（二）游戏获胜问题
（三）普查疾病
（四）根源问题
考点八 贝叶斯公式的应用
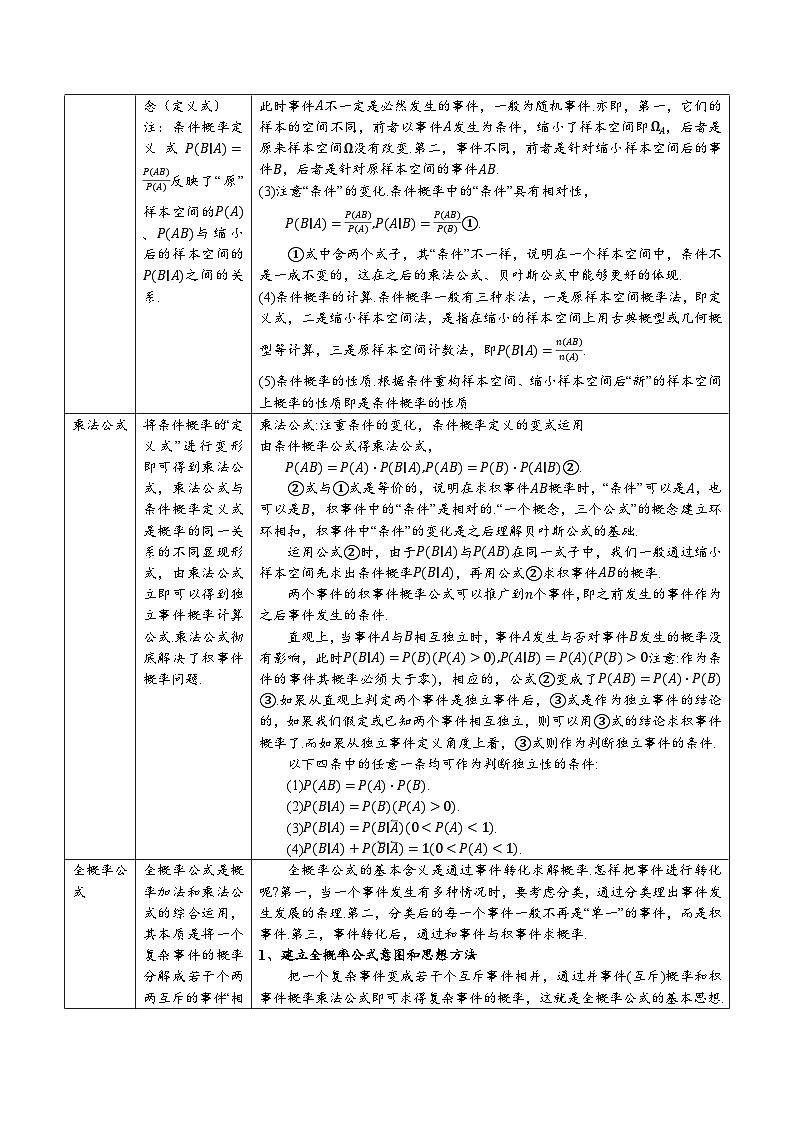
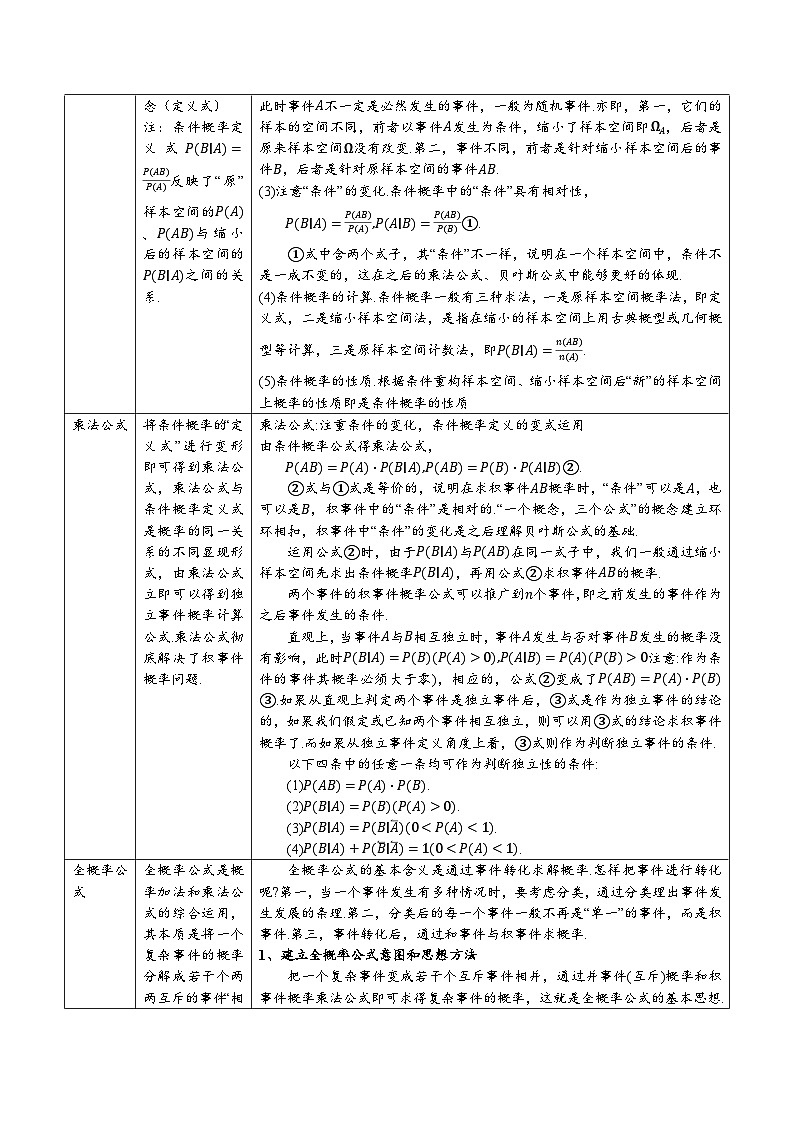
1、一个概念三个公式
条件概率
条件概率是理解并进行复杂概率运算的基础，乘法公式、全概率公式和贝叶斯公式是条件概率的应用和拓展.条件概率的本质是缩小样本空间后的事件概率，通过古典概型(或其他概型)，抽象概括成条件概率的概念（定义式）
注：条件概率定义式P(B∣A)=P(AB)P(A)反映了“原”样本空间的P(A)、P(AB)与缩小后的样本空间的P(B∣A)之间的关系.
条件概率概念的建立要抓住“事件”和“空间”进行分析，要分析“条件”是必然性还是“随机”性，是以“条件”重构的样本空间还是在原样本空间中运用“条件”.因此，“事件”“空间”和“条件”是概念建立的关键词.
(1)对条件A的理解：第一，从缩小样本空间的角度上看，在条件“已经发生”的基础上，样本空间缩小了，是在缩小了的空间上用概率模型或概率计算方法求解概率.第二，从概率之间的相互联系分析，在事件A发生的条件下，事件B发生的概率P(B∣A)又与在原样本空间上事件A发生的概率P(A)有关系，正因为此时的P(A)是事件A在原样本空间发生的概率，因而事件A在原样本空间里不是“必然发生”的事件，不是“发生过了”的事件，而是随机事件.
(2)对P(B∣A)和P(AB)的分析.学生容易混淆P(B∣A)和P(AB)，认为它们都是“事件A发生了，事件也B发生了”，实际上，它们有着本质的区别.第一，前者指缩小样本空间后事件B发生的概率，此时，事件A已经发生了，以A发生为条件重新组构样本空间.第二，后者指原样本空间上事件A、B同时发生的概率，此时事件A不一定是必然发生的事件，一般为随机事件.亦即，第一，它们的样本的空间不同，前者以事件A发生为条件，缩小了样本空间即ΩA，后者是原来样本空间Ω没有改变.第二，事件不同，前者是针对缩小样本空间后的事件B，后者是针对原样本空间的事件AB.
(3)注意“条件”的变化.条件概率中的“条件”具有相对性，
P(B∣A)=P(AB)P(A),P(A∣B)=P(AB)P(B)①.
①式中含两个式子，其“条件”不一样，说明在一个样本空间中，条件不是一成不变的，这在之后的乘法公式、贝叶斯公式中能够更好的体现.
(4)条件概率的计算.条件概率一般有三种求法，一是原样本空间概率法，即定义式，二是缩小样本空间法，是指在缩小的样本空间上用古典概型或几何概型等计算，三是原样本空间计数法，即P(B∣A)=n(AB)n(A).
(5)条件概率的性质.根据条件重构样本空间、缩小样本空间后“新”的样本空间上概率的性质即是条件概率的性质
乘法公式
将条件概率的“定义式”进行变形即可得到乘法公式，乘法公式与条件概率定义式是概率的同一关系的不同显现形式，由乘法公式立即可以得到独立事件概率计算公式.乘法公式彻底解决了积事件概率问题.

乘法公式:注重条件的变化，条件概率定义的变式运用
由条件概率公式得乘法公式，
P(AB)=P(A)⋅P(B∣A),P(AB)=P(B)⋅P(A∣B)②.
②式与①式是等价的，说明在求积事件AB概率时，“条件”可以是A，也可以是B，积事件中的“条件”是相对的.“一个概念，三个公式”的概念建立环环相扣，积事件中“条件”的变化是之后理解贝叶斯公式的基础.
运用公式②时，由于P(B∣A)与P(AB)在同一式子中，我们一般通过缩小样本空间先求出条件概率P(B∣A)，再用公式②求积事件AB的概率.
两个事件的积事件概率公式可以推广到n个事件，即之前发生的事件作为之后事件发生的条件.
直观上，当事件A与B相互独立时，事件A发生与否对事件B发生的概率没有影响，此时P(B∣A)=P(B)(P(A)>0),P(A∣B)=P(A)(P(B)>0注意:作为条件的事件其概率必须大于零)，相应的，公式②变成了P(AB)=P(A)⋅P(B)③.如果从直观上判定两个事件是独立事件后，③式是作为独立事件的结论的，如果我们假定或已知两个事件相互独立，则可以用③式的结论求积事件概率了.而如果从独立事件定义角度上看，③式则作为判断独立事件的条件.
以下四条中的任意一条均可作为判断独立性的条件:
(1)P(AB)=P(A)⋅P(B).
(2)P(B∣A)=P(B)(P(A)>0).
(3)P(B∣A)=P(B∣A)(0