初中数学人教版九年级上册第二十二章 二次函数22.3 实际问题与二次函数精品同步练习题

这是一份初中数学人教版九年级上册第二十二章 二次函数22.3 实际问题与二次函数精品同步练习题，文件包含重难点讲义人教版数学九年级上册-基础练223实际问题与二次函数原卷版docx、重难点讲义人教版数学九年级上册-基础练223实际问题与二次函数解析版docx等2份试卷配套教学资源，其中试卷共50页， 欢迎下载使用。

2022-2023学年九年级数学上册考点必刷练精编讲义（人教版）基础
第22章《二次函数》
22.3 实际问题与二次函数

知识点01：二次函数的实际应用—几何问题
1．（2020九上·朝阳期末）正方体的棱长为x，表面积为y，则y与x之间的函数关系式为 （　　）
A． B． C． D．
【答案】C
【完整解答】解：∵正方体有6个表面，
∴y=6x2，
∴y与x关系式为y=6x2，
故答案为：C

【思路引导】根据正方体表面积的计算方法列函数表达式即可。
2．（2021九上·密云期末）如图，一个矩形的长比宽多3cm，矩形的面积是Scm2．设矩形的宽为xcm，当x在一定范围内变化时，S随x的变化而变化，则S与x满足的函数关系是（　　）

A．S=4x+6 B．S=4x-6 C．S=x2+3x D．S=x2-3x
【答案】C
【完整解答】解：设矩形的宽为xcm，则长为（x+3）cm
由题意得：S=x（x+3）=x2+3x.
故答案为：C.

【思路引导】设矩形的宽为xcm，则长为（x+3）cm，根据矩形的面积公式可得S=x（x+3）=x2+3x.
3．（2021九上·浦东期末）在一个边长为2的正方形中挖去一个小正方形，使小正方形四周剩下部分的宽度均为x，若剩下阴影部分的面积为y，那么y关于x的函数解析式是　 　．
【答案】
【完整解答】解：设剩下部分的面积为y，则：
y=4-(2-2x)²=-4x2+8x（0＜x＜1），
故答案为：．

【思路引导】根据题意设剩下部分的面积为y，即可得出y关于x的函数解析式。
4．（2021九上·普宁期末）用长12m的铝合金条制成矩形窗框（如图所示），那么这个窗户的最大透光面积是　 　（中间横框所占的面积忽略不计）

【答案】6m2
【完整解答】解：设窗户竖着的边长长为米，横着的边长为米，

当时，取得最大值，为6
故答案为：6m2
【思路引导】先求出，再计算求解即可。
5．（2021九上·临海期末）如图，Rt△ABC中，∠ACB=90°，AC=BC=2，点P是AB上一动点，连接CP，将线段CP绕点C顺时针旋转90°得到线段CQ，连接PQ，AQ，则△PAQ面积的最大值为　 　.

【答案】1
【完整解答】解：如图，将线段CP绕点C顺时针旋转90°得到线段CQ，

∴∠PCQ=90°，CP=CQ，
∴∠ACP+∠ACQ=90°，
又∵∠ACB=90°，
∴∠BCP+∠ACP=90°，
∴∠BCP=∠ACP，
∵AC=BC，
∴△BPC≌△AQC（SAS），
∴∠B=∠CAQ，BP=AQ，
∵BC=AC=2，
∴∠B=∠CAQ=∠BAC=45°，
∴∠PAQ=∠BAC+∠CAQ=90°，
在Rt△ABC中，由勾股定理AB= ，
设BP=AQ=x，则 ，
∴ ，
∵ ，函数开口向下，函数有最大值，
当 时， .
故答案为：1.

【思路引导】利用旋转的性质可证得∠PCQ=90°，CP=CQ，利用余角的性质可得到∠BCP=∠ACP，利用SAS证明△BPC≌△AQC，利用全等三角形的对应边和对应角相等，可证得∠B=∠CAQ，BP=AQ；再证明∠PAQ-90°，利用勾股定理求出AB的长；设BP=AQ=x，可表示出AP的长，利用三角形的面积公式可得到△PAQ与x之间的函数解析式，将函数解析式转化为顶点式，利用二次函数的性质，可求出△PAQ的最大面积.
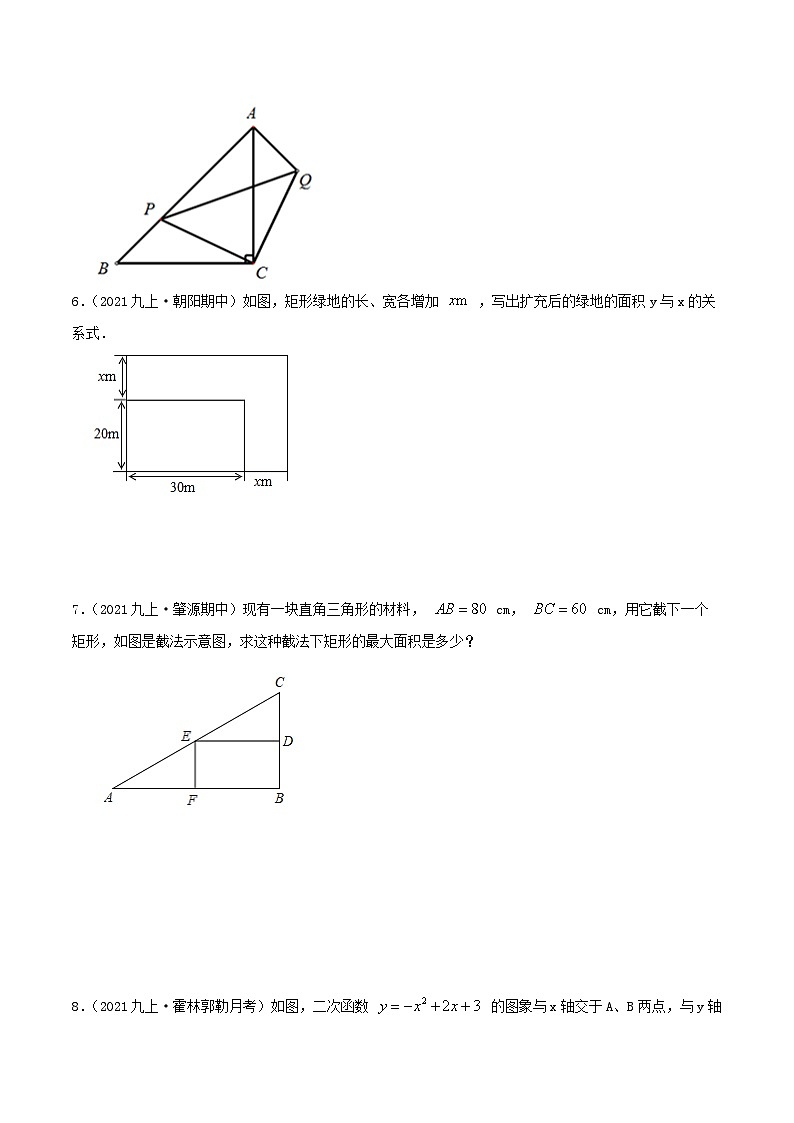
6．（2021九上·朝阳期中）如图，矩形绿地的长、宽各增加 ，写出扩充后的绿地的面积y与x的关系式．

【答案】解：∵矩形原来的长和宽分别为30m、20m，矩形绿地的长、宽各增加xm，
∴增加后的矩形的长和宽分别为（20+x）m，（30+x）m，
∴ .
【思路引导】根据矩形原来的长和宽分别为30m、20m，矩形绿地的长、宽各增加xm，得出增加后的矩形的长和宽分别为（20+x）m，（30+x）m，即可得出扩充后的绿地的面积y与x的关系式．
7．（2021九上·肇源期中）现有一块直角三角形的材料， cm， cm，用它截下一个矩形，如图是截法示意图，求这种截法下矩形的最大面积是多少？

【答案】解：∵四边形BFED是矩形，
∴EF∥CB，
∴ ，
∵ ，
∴△AEF∽△ACB，
∴ ，
∵ cm， cm，
设 ，则 ，
∴ ，
∴ ，
∴ （ ），
∴当 时，S有最大值 ；
∴这种截法下矩形的最大面积是1200 cm2．
【思路引导】先求出 △AEF∽△ACB， 再利用相似三角形的性质计算求解即可。
8．（2021九上·霍林郭勒月考）如图，二次函数 的图象与x轴交于A、B两点，与y轴交于点C，顶点为D，求 的面积．

【答案】解：延长DC交x轴于E，

依题意，可得y＝−x2＋2x＋3＝−（x−1）2＋4，
∴顶点D（1，4），
令y＝0，可得x＝3或x＝−1，
∴B（3，0），
令x＝0，可得y＝3，
∴C（0，3），
∴OC＝3，
∴直线DC的解析式为y＝x＋3，
令y＝0，可得x＝-3，
∴E（-3，0），
BE＝6，
∴S△BCD＝S△BED−S△BCE＝ =12-9=3．
∴△BCD的面积为3．
【思路引导】 延长DC交x轴于E， 根据二次函数的解析式求出顶点坐标，再利用割补法 S△BCD＝S△BED−S△BCE求解即可。
知识点02：二次函数的实际应用—销售问题
9．（2021九上·北仑期中）某店销售一款运动服，每件进价100元，若按每件128元出售，每天可卖出100件，根据市场调查结果，若每件降价1元，则每天可多卖出5件，要使每天获得的利润最大，则每件需要降价（　　）
A．3元 B．4元 C．5元 D．8元
【答案】B
【完整解答】解：设每件需要降价x元，每天获得的利润为W，根据题意得
W=（128-x-100）（100+5x）=-5（x-4）2+2880，
∵-5＜0，
∴当x=4时，W最大值=2880.
故答案为：B.
【思路引导】设每件需要降价x元，每天获得的利润为W，根据W=每一件的利润×销售量，列出W与x之间的函数解析式，将其函数解析式转化为顶点式，利用二次函数的性质，可求出结果.
10．（2021九上·淮北月考）某超市销售一种商品，每件成本为50元，销售人员经调查发现，该商品每月的销售量 （件）与销售单价 （元）之间满足函数关系式 ，若要求销售单价不得低于成本，为每月所获利润最大，该商品销售单价应定为多少元？每月最大利润是多少？（　　）
A．90元，4500元 B．80元，4500元
C．90元，4000元 D．80元，4000元
【答案】B
【完整解答】解：设每月总利润为 ，
依题意得：



，此图象开口向下，又 ，
当 时， 有最大值，最大值为4500元．
故答案为：B．

【思路引导】根据题意，列出二次函数，根据二次函数的最值求出答案即可。
11．（2021九上·河池期中）某文具店出售某种文具盒，若每个获利 元，一天可售 个，则当 　 　元时，一天出售这种文具盒的总利润 最大.
【答案】5
【完整解答】解：由题意，得
y＝x（10−x）＝−x2＋10x＝−（x−5）2＋25，
当x＝5时，y最大＝25，
故当 5元时，一天出售这种文具盒的总利润 最大
故答案为：5.

【思路引导】 根据每个获利 元，一天可售 个，结合“总利润=单件利润×数量”列函数时，再根据二次函数性质求最大值即可.
12．（2021九上·南通月考）某商店经营一种水产品，成本为每千克40元的水产品，据市场分析，若按每千克50元销售，一个月能售出500千克；销售价每涨1元，月销售量就减少10千克，针对这种水产品的销售情况，销售单价定为　 　元时，获得的利润最多.
【答案】70
【完整解答】解：设销售单价定为每千克x元，获得利润为y元，则：
y=（x-40）[500-（x-50）×10]，
=（x-40）（1000-10x），
=-10x2+1400x-40000，
=-10（x-70）2+9000，
∴当x=70时，利润最大为9000元.
故答案为：70.
【思路引导】设销售单价定为每千克x元，获得利润为y元，利用利润=每件的利润×销售量列出式子，再化为顶点式，再根据二次函数的性质即可得出答案.
13．（2021九上·长兴月考）某宾馆共有80间客房.宾馆负责人根据经验作出预测：今年7月份，每天的房间空闲数y（间）与定价x（元/间）之间满足y＝ x﹣42（x≥168）.若宾馆每天的日常运营成本为5000元，有客人入住的房间，宾馆每天每间另外还需支出28元的各种费用，宾馆想要获得最大利润，同时也想让客人得到实惠，应将房间定价确定为　 　元.
【答案】256
【完整解答】解：设每天的利润为W元，根据题意，得：
W＝（x﹣28）（80﹣y）﹣5000
＝（x﹣28）[80﹣（ x﹣42）]﹣5000
＝﹣ x2+129x﹣8416
＝﹣ （x﹣258）2+8225，
∵当x＝258时，y＝ ×258﹣42＝22.5，不是整数，
∴当x＝256或x＝260时，函数取得最大值，最大值为8224元，
又∵想让客人得到实惠，
∴x＝260（舍去）
∴宾馆应将房间定价确定为256元时，才能获得最大利润，
故答案为：256.
【思路引导】设每天的利润为W元，根据总利润=每个房间的利润×入住房间的数量-每日的运营成本，列出函数关系式，再利用配方化为顶点式，然后根据二次函数的性质求解即可.
14．（2021九上·河池期中）某商店购进一批单价为20元的日用商品，如果以单价30元销售，那么半月内可售出400件，根据销售经验，提高销售单价会导致销售量的减少，即销售单价每提高1元，销售量相应减少20件，如果提高售价，请问将售价定每件为多少元时，才能在半月内获得最大利润？并求出最大利润.
【答案】解：设售价定每件为 元，利润为 元，依题意可得
，
整理得 ，
配方得 ，
∵-20＜0，
∴当 时， 的最大值为4500元.
答：售价定为每件35元时，才能在半月内获得最大利润，最大利润为4500元.
【思路引导】 设售价定每件为 元，利润为 元，根据“利润=单件利润×销售量”求得函数关系式，然后利用二次函数的性质求最大值即可.
15．（2021九上·拱墅期中）某商家销售一款商品，该商品的进价为每件80元，现在的售价为每件145元，每天可销售40件.商场规定每销售一件需支付给商场管理费5元，通过市场调查发现，该商品单价每降1元，每天销售量增加2件.若每件商品降价x元，每天的利润为y元，请完成以下问题的解答.
（Ⅰ）用含x的式子表示：①每件商品的售价为 ▲ 元；②每天的销售量为 ▲ 件；
（Ⅱ）求出y与x之间的函数关系式，并求出售价为多少时利润最大？最大利润是多少元？
【答案】解：（I）（145﹣x）；
（Ⅱ）（40+2x）；（II）根据题意可得：y＝（145﹣x﹣80﹣5）（2x+40），
＝﹣2x2+80x+2400，
＝﹣2（x﹣20）2+3200，
∵a＝﹣2＜0，
∴函数有最大值，
∴当x＝20时，y有最大值为3200元，此时售价为145﹣20＝125元，
∴售价为125元时利润最大，最大利润是3200元.
【完整解答】解：（I）由题意可知：①每件商品的售价为：（145﹣x）元；
②每天的销售量为：（40+2x）件；
故答案为：①（145﹣x），②（40+2x）；
【思路引导】（1）①利用开始的售价减去降低的钱数即为售价；
②首先表示出增加的件数，然后加上40即可；
（2）根据每天的总利润=每件商品的利润乘以每天的销售数量建立函数关系式，对其进行化简，然后结合二次函数的性质进行求解.
16．（2021九上·沙依巴克期末）某百货商店服装在销售过程中发现，某品牌童装平均每天可售出20件，每件盈利40元，经市场调查发现，在进货不变的情况下，若每件童装每降价1元，日销售量将增加2件，当每件童装降价多少元时，这种童装一天的销售利润最多？最多利润是多少？
【答案】解：设每件童装降价x元，利润为y元，

，
∴当 时，y取得最大值，此时 ，
即每件童装降价15元时，每天销售这种童装的利润最高，最高利润是1250元.
【思路引导】设每件童装降价x元，利润为y元，利用利润y=每一件的利润×销售量，可得到y与x之间的函数解析式，再将函数解析式转化为顶点式，利用二次函数的性质可求解.
17．（2021九上·舟山期末）某公司今年国庆期间在网络平台上进行直播销售猕猴桃，已知猕猴桃的成本价格为8元／kg，经销售发现：每日销售量y（kg）与销售单价x（元／kg）满足一次函数关系，下表记录的是有关数据，销售单价不低于成本价且不高于24元／kg．设公司销售猕猴桃的日获利为w（元）.
x（元／kg）
9
10
11
y(kg)
2100
2000
1900
（1）请求出日销售量y与销售单价x之间的函数关系式；
（2）当销售单价定为多少时，销售这种猕猴桃日获利w最大？最大利润为多少元？
【答案】（1）解：设y=kx+b
则
∴
∴
（2）解：由题意得：

∴对称轴为x=19
∵，a=-100<0
∴当x=19，即 销售单价定为19时，销售这种猕猴桃日获利w最大，最大利润为12100元.
【思路引导】（1）由待定系数法，得出结果。
（2）由二次函数配方法，得出，从而得出结果。
知识点03：二次函数的实际应用—拱桥问题
18．图2是图1中拱形大桥的示意图，桥拱与桥面的交点为O，B，以点O为原点，水平直线OB为 轴，建立平面直角坐标系，桥的拱形可以近似看成抛物线 ，桥拱与桥墩AC的交点C恰好在水面，有AC⊥ 轴。若OA=10米，则桥面离水面的高度AC为（　　）

A． 米 B． 米 C． 米 D． 米
【答案】B
【完整解答】解：根据题意，由AC⊥x轴，OA=10米，可知点C的横坐标为-10，然后把x=-10代入函数的解析式 ，即C点为（-10，- ），因此可知桥面离水面的高度AC为 m.
故答案为：B.
【思路引导】由AC⊥x轴可知点C的横坐标与点A的横坐标相同即为-10，把点C的横坐标代入解析式即可求点C的纵坐标，即桥面离水面的高度。
19．（2020九上·天长期末）河北省赵县的赵州桥的桥拱是近似的抛物线形，建立如图所示的平面直角坐标系，其函数的关系式为y=﹣x2，当水面离桥拱顶的高度DO是4m时，这时水面宽度AB为（　　）

A．﹣20m B．10m C．20m D．﹣10m
【答案】C
【完整解答】根据题意B的纵坐标为﹣4，
把y=﹣4代入y=﹣​x2，
得x=±10，
∴A（﹣10，﹣4），B（10，﹣4），
∴AB=20m．
即水面宽度AB为20m．
故选C．
【思路引导】根据题意，把y=﹣4直接代入解析式即可解答．
20．如图，小河上有一拱桥，拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE，ED，DB组成，已知河底ED是水平的，ED=16m，AE=8m，抛物线的顶点C到ED的距离是11m．试以ED所在的直线为x轴，抛物线的对称轴为y轴建立平面直角坐标系，求题中抛物线的函数表达式　 　．

【答案】y=﹣ x2+11
【完整解答】解：如图所示．

由题知抛物线的顶点坐标为（0，11），B（8，8），
设抛物线的表达式为y=ax2+11，
将点B的坐标（8，8）代入抛物线的表达式得： ，
所以抛物线的表达式为：y=﹣ x2+11．
【思路引导】由题知抛物线的顶点坐标为（0，11），B（8，8），代入抛物线的解析式求出解析式
21．（2021九上·北京月考）如图是抛物线形拱桥，当水面宽为4米时，拱顶距离水面2米；当水面高度下降1米时，水面宽度为多少米？请你以点D为原点、 所在直线为x轴建立平面直角坐标系，解决这个实际问题．

【答案】解：如图，以D为坐标原点， 所在的直线为x轴建立直角坐标系，

结合题意可得：
且C为抛物线的顶点，
设抛物线为：


所以抛物线的解析式为：
当水面高度下降1米时，即


解得：
所以水面宽度为： ，
答：水面下降1米，此时水面宽度为 米.
【思路引导】 以D为坐标原点， 所在的直线为x轴建立直角坐标系， 根据题意求出抛物线的解析式，然后求出当y=-1，求出x的值即可得出答案。
22．（2021九上·厦门期中）如图，拱门的地面宽度为200米，两侧距地面高150米处各有一个观光窗，两窗的水平距离为100米，求拱门的最大高度.

【答案】解：如图所示，以CD所在直线为x轴，CD的垂直平分线为y轴建立平面直角坐标系，

∵CD＝200，
∴抛物线与 轴的交点为 ， ，
∴设这条抛物线的解析式为 ，
∵AB＝100，AB与CD的距离为150，
∴点B的坐标为（50，150），
抛物线经过点 ，
，
解得： ，
，
当 时， 取得最大值，此时 ，
即拱门的最大高度是200米.
【思路引导】以CD所在直线为x轴，CD的垂直平分线为y轴建立平面直角坐标系，易得C（-100，0），D（100，0），B（50，150），设抛物线的解析式为y=a(x-100)(x+100)，然后将点B坐标代入求出a的值，得到抛物线的解析式，进而可得拱门的最大高度.
23．（2021九上·海州期末）如图，某公路隧道横截面为抛物线，其最大高度6米，底部宽度OM为12米，现以O点为原点，OM所在的直线为x轴建立直角坐标系.

（1）求这条抛物线的解析式；
（2）若要搭建一个由AD﹣DC﹣CB组成的矩形“支撑架”，已知支架的高度为4米，则这个“支撑架”总长是多少米？
【答案】（1）解：由题意，该抛物线过O（0，0）、M（12，0），
∴该抛物线的对称轴为直线x=6，顶点坐标为P（6，6），
设该抛物线的解析式为y=a(x－6)2+6，
将点O(0，0)代入，得：36a+6=0，解得：a= ，
∴该抛物线的解析式为y= (x－6)2+6= x2+2x；
（2）解：∵AD﹣DC﹣CB组成的是矩形“支撑架”，
∴AD=CB=4，
令y=4，由4= x2+2x得：x2－12x+24=0，
解得： ， ，
∴C( ，4)，D（ ，4），
∴CD= －( )= ，
∴AD+DC+CB=4+4+ =8+ ，
∴这个“支撑架”总长是（8+ ）米.
【思路引导】（1）由题意可知该抛物线过O（0，0）、M（12，0），求出中点坐标可得对称轴以及顶点坐标，设该抛物线的解析式为y=a(x-6)2+6，将O（0，0）代入求出a的值，据此可得抛物线的解析式；
（2）由题意可得AD=CB=4，令y=4，求出x的值，可得点C、D的坐标，然后求出CD，接下来求出AD+DC+CB即可.
24．（2021九上·番禺期末）如图是抛物线型拱桥，当拱顶离水面2米时，水面宽4米．

（1）以抛物线的顶点为原点，抛物线的对称轴为y轴建立直角坐标系，请在图中画出坐标系，并求出抛物线的解析式；
（2）当水面下降1米时，水面宽度增加了多少米？
【答案】（1）解：建立平面直角坐标系如图所示，

由题意可得：顶点坐标为，
设抛物线的解析式为，
把点坐标代入得出：，
所以抛物线解析式为；
（2）解：当水面下降1米，
即当时，对应的抛物线上两点之间的距离，也就是直线与抛物线相交的两点之间的距离，
可以通过把代入抛物线解析式得出：
，
解得：，
所以水面宽度增加到米，
答：当水面下降1米时，水面宽度增加了米．
【思路引导】（1）根据已知得出直角坐标系进而求出二次函数解析式；
（2）通过把y=-1带入抛物线解析式，得出水面宽度即可得出答案。
25．（2021九上·温岭期中）有一个抛物线型蔬菜大棚，将其截面放在如图所示的平面直角坐标系中，抛物线可以用函数y＝ax2+bx来表示，已知OA＝8米，距离O点2米处的棚高BC为 米.

（1）求该抛物线的解析式；
（2）若借助横梁DE（DE∥OA）建一个门，要求门的高度为1.5米，求横梁DE的长度是多少米？
【答案】（1）解：由题意可得，抛物线经过（2， ），（8，0），
故 ，
解得： ，
故抛物线解析式为：y＝ x2+ x；
（2）解：由题意可得：当y＝1.5时，
1.5＝ x2+ x，
解得：x1＝4+2 ，x2＝4﹣2 ，
故DE＝x1﹣x2＝4+2 ﹣（4﹣2 ）
＝4 .
【思路引导】（1）由图知，抛物线经过点（2，），（8，0），用待定系数法可求解；
（2）由题意把y=1.5代入（1）中的解析式可得关于x的方程，解方程求得x的值，然后由线段的构成DE=x1-x2可求解.
知识点04：二次函数的实际应用—抛球问题
26．（2021九上·温岭期中）小敏在某次投篮中，篮球的运动路线是抛物线 3.5的一部分（如图），若命中篮圈中心，则他与篮底的水平距离 是（　　）

A．3.5m B．3.8m C．4m D．4.5m
【答案】C
【完整解答】解：如图，把y=3.05代入函数 ，解得x=1.5或x=－1.5（舍去）
则l=2.5+1.5=4（m）
故答案为：C.
【思路引导】由题意把y=3.05代入解析式可得关于x的方程，解方程可求得x的值，再根据小敏与篮底的水平距离=2.5+x可求解.
27．2011年5月22日—29日在美丽的青岛市举行了苏迪曼杯羽毛球混合团体锦标赛.在比赛中，某次羽毛球的运动路线可以看作是抛物线y=－ x2+bx+c的一部分（如图），其中出球点B离地面O点的距离是1m，球落地点A到O点的距离是4m，那么这条抛物线的解析式是（　　）

A． B．
C． D．
【答案】A
【完整解答】解：∵出球点B离地面O点的距离是1m，球落地点A到O点的距离是4m，
∴B点的坐标为：（0，1），A点坐标为（4，0），
将两点代入解析式得： ，
解得： ,
∴这条抛物线的解析式是：y=
故答案为：A.
【思路引导】根据题意可得点B（0,1）点A（4,0），代入用待定系数法求解即可。
28．一小球被抛出后，距离地面的高度h（米）和飞行时间t（秒）满足下列函数解析式：h=﹣3（t﹣2）2+5，则小球距离地面的最大高度是（　　）
A．2米 B．3米 C．5米 D．6米
【答案】C
【完整解答】解：∵h=﹣3（t﹣2）2+5，
∴当t=2时，h取得最大值，此时h=5，
故选C．
【思路引导】根据二次函数的解析式，可以得到二次函数的最大值，从而可以解答本题．
29．（2021九上·南京月考）如图，某运动员推铅球，铅球行进高度 与水平距离 之间的关系是 ，则此运动员将铅球推出的距离是　 　m.

【答案】12
【完整解答】解：∵ ，
∴当y=0时， ，
解得x1=12，x2=-2（舍去），
∴此运动员将铅球推出的距离是12m.
故答案为：12.
【思路引导】由题意可知y=0，可得到关于x的方程，解方程求出x的值，可得到此运动员将铅球推出的距离.
30．（2021九上·安康月考）小明在某次投篮中，球的运动路线是抛物线y＝－ x2＋3.5的一部分(如图所示)，若命中篮圈中心，则他与篮底的距离l是　 　m.

【答案】4
【完整解答】解：将y=3.05代入y＝－ x2＋3.5，得
3.05=－ x2+3.5，
解得，x=−1.5(舍去)或x=1.5，
∴若命中篮圈中心，则他与篮底的距离l是：2.5+1.5=4(m)，
故答案为：4.
【思路引导】由题意把y=3.05代入解析式可得关于x的一元二次方程，解方程可求解.
31．（2021九上·江油期末）如图是足球守门员在O处开出一记手抛高球后足球在空中运动到落地的过程，它是一条经过A、M、C三点的抛物线．其中A点离地面1.4米，M点是足球运动过程中的最高点，离地面3.2米，离守门员的水平距离为6米，点C是球落地时的第一点．那么足球第一次落地点C距守门员的水平距离为　 　米．

【答案】14
【完整解答】解：根据题意得，抛物线的顶点坐标为M（6，3.2），经过点A（0，1.4），
∴设抛物线的解析式为y=a（x-6）2+3.2，
把点A（0，1.4）的坐标代入y=a（x-6）2+3.2，得36a+3.2=1.4，
∴a=-，
∴抛物线的解析式为y=-（x-6）2+3.2，
令y=0，则-（x-6）2+3.2=0，
∴x=14或x=-2（不符合题意，舍去）
∴点C的坐标为（14，0），
∴点C距守门员的水平距离为14米.
故答案为：14.
【思路引导】根据题意设抛物线的解析式为y=a（x-6）2+3.2，利用待定系数法求出抛物线的解析式，再求出抛物线与x轴的交点C的坐标，即可得出答案.
32．（2020九上·青岛期末）在“学习一项体育技能”活动中，小明作为学生代表去观看“青岛黄海足球队”的训练．他看到队员们在做掷界外球训练，甲球员要将足球掷给离他7.5米远的乙球员，掷出足球的运行轨还是一条抛物线，足球行进的高度y（米）与水平距离x（米）之间的关系如图所示，足球出手时离地面的高度为2米，在距离甲球员4米处达到最大高度3.6米．若不计其他因素，身高1.85米的乙球员要能触到足球，他垂直起跳的高度至少要达到多少米？

【答案】解：根据题意可知抛物线的顶点坐标为 ，
与抛出点的坐标为 ，
设抛物线的解析式为： ，
顶点坐标代入得： ，
抛出点坐标代入得： ，
解得： ，
∴抛物线得解析式为： ，
当 时， ，
米，
故他垂直起跳的高度至少要达到0.525米．
【思路引导】设抛物线的解析式为： ，根据题意中给出的顶点坐标以及抛出点的坐标，求得解析式，带入解析式可得出答案。
33．（2020九上·舒兰期末）从地面竖直向上抛出一小球，小球的高度 (单位： )与小球的运动时间 (单位： )之间的关系式是 ( )．求小球运动时间是多少时，小球最高？小球运动中的最大高度是多少？
【答案】解：


当 时， 最大 ．
答：小球运动3秒时，小球最高，最大高度是 ．
【思路引导】首先将二次函数转换成顶点式，然后即可求出自变量和函数值的最大值.
34．（2021九上·青岛期末）“福虎迎冬奥”明溪喜迎冬奥篮球赛火热开启，运动员你攻我守，分秒必争，篮球运动员小明站在点O处长抛球，球从离地面1米的A处扔出，篮球在距O点6米的B处达到最高点，最高点C距地面4米，又一次弹起，落到点E处，EF之间的距离为2米，据试验，篮球在场地上第二次弹起后划出的抛物线与第一次划出的抛物线形状相同，但最大高度减少到原来最大高度的一半，以小明站立处O为坐标原点，建立平面直角坐标系如图所示．（算出的结果均保留整数，≈1.75；≈2.5）

（1）求抛物线ACD的函数表达式；
（2）篮球第二次落地点E距O点的距离；
（3）若小明需要在第一次抛球时投中篮筐，他应该向前走多远？
【答案】（1）解：设篮球开始飞出到第一次落地时抛物线的表达式为y=a（x-h）2+k，
∵h=6，k=4，
∴y=a（x-6）2+4，
由已知：当x=0时y=1，
即1=36a+4，
∴a=，
∴表达式为y=（x-6）2+4；
（2）解：令y=0，（x-6）2+4=0，
∴（x-6）2=48，
解得：x1=4+6≈13，x2=-4+6，
∴点D坐标为(13，0)．
∴OD=13m
如图所示，过抛物线DE的顶点M作MG∥x轴，交抛物线ACD于点G、点H．

∵篮球在场地上第二次弹起后划出的抛物线与第一次划出的抛物线形状相同，但最大高度减少到原来最大高度的一半
∴抛物线DME相当于将抛物线ACD向下平移的两个长度单位再向右平移．
∴GH=DE，点G、H、M的纵坐标为2．
当y=2时，（x-6）2+4=2
x1= x2=
∴DE=GH=x2-x1=10
OE=OD+DE
=13+10
=23m
∴篮球第二次落地点E距O点的距离23m
（3）解：如图所示，当y=3时，（x-6）2+4＝3，

解得：x1=；x2=9
即点OR=9m，
∵EF=2m
∴OF=OE+EF=23+2=25m
若小明需要在第一次抛球时投中篮筐，他应该向前走的距离为：
RF=OF-OR=25-9=16m
故：若小明需要在第一次抛球时投中篮筐，他应该向前走16m．
【思路引导】（1）根据顶点坐标为（6，4），可设顶点式，再将点A带入即可；
（2）令y=0可求出x的两个值，在安世纪情况筛选；
（3）如图可得出第二次篮球弹出后的距离为DE，相当于将抛物线AMCND向下平移2个单位得出x的值即可得出DE的值，即可得出答案。
知识点05：二次函数的实际应用—喷水问题
35．（2020九上·瑶海月考）如图，用水管从某栋建筑物2.25m高的窗口A 处向外喷水，喷的水流呈抛物线型（抛物线所在平面与墙面垂直），如果抛物线的最高点M离墙1米，离地面3米，则水流下落点B离墙的距离OB是（　　）

A．2.5米 B．3米 C．3.5米 D．4米
【答案】B
【完整解答】由题意可得，抛物线的顶点坐标为（1，3），设抛物线的解析式为：y=a（x-1）2+3，即2.25=a（0-1）2+3，解得a=-0.75，∴y= （x-1）2+3，当y=0时， （x-1）2+3=0，解得，x1=-1，x2=3，∴点B的坐标为（3，0），∴OB=3，答：水流下落点B离墙距离OB的长度是3米．
故答案为：B．
【思路引导】根据题意求出抛物线的解析式，从而求出点B的坐标进行解答即可。
36．（2021九上·和平期末）如图，要修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高，高度为3m，水柱落地处离池中心3m，水管的长为（　　）

A． B． C． D．
【答案】A
【完整解答】解：由题意可知点（1，3）是抛物线的顶点，
∴设这段抛物线的解析式为y=a（x-1）2+3．
∵该抛物线过点（3，0），
∴0=a（3-1）2+3，
解得：a=-．
∴y=-（x-1）2+3．
∵当x=0时，y=-（0-1）2+3=-+3=，
∴水管应长m．
故答案为：A

【思路引导】由题意可知点（1，3）是抛物线的顶点，可设顶点式为y=a（x-1）2+3，将（3，0）代入解析式中求出a值即得解析式，再求出x=0时的y值即可.
37．（2021九上·长兴月考）学校卫生间的洗手盘台面上有一瓶洗手液（如图①）.小丽经过测量发现：洗手液瓶子的截面图下部分是矩形CGHD，洗手液瓶子的底面直径GH＝12cm，D，H与喷嘴位置点B三点共线.当小丽按住顶部A下压至如图②位置时，洗手液从喷口B流出（此时喷嘴位置点B距台面的距离为16cm），路线近似呈抛物线状，小丽在距离台面15cm处接洗手液时，手心Q到直线DH的水平距离为4cm，若小丽不去接，则洗手液落在台面的位置距DH的水平距离是16cm.根据小丽测量所得数据，可得洗手液喷出时的抛物线函数解析式的二次项系数是（　　）

A．﹣ B． C．﹣ D．
【答案】C
【完整解答】解：根据题意：
GH所在直线为x轴，GH的垂直平分线所在直线为y轴建立如图所示的平面直角坐标系，
喷口B为抛物线顶点，共线的三点B、D、H所在直线为抛物线的对称轴，

根据题意，OH＝6，B（6，16），Q（10，15），
设抛物线解析式为y＝a（x﹣6）2+16，
把Q（10，15）代入解析式得：15＝a（10﹣6）2+16，
解得：a＝﹣ ，
故答案为：C.
【思路引导】如图以GH所在直线为x轴，GH的垂直平分线所在直线为y轴建立如图所示的平面直角坐标系，喷口B为抛物线顶点，共线的三点B、D、H所在直线为抛物线的对称轴，然后写出顶点B及Q的坐标，利用顶点式求出抛物线解析式即可.
38．（2021九上·丰台期末）中国跳水队在第三十二届夏季奥林匹克运动会上获得7金5银12枚奖牌的好成绩．某跳水运动员从起跳至人水的运动路线可以看作是抛物线的一部分．如图所示，该运动员起跳点A距离水面10m，运动过程中的最高点B距池边2.5m，入水点C距池边4m，根据上述信息，可推断出点B距离水面　 　m．

【答案】
【完整解答】解：建立平面直角坐标系如图：

根据题意可知，点A的坐标为（3，10），点C的坐标为（5，0），抛物线的对称轴为直线x=3.5，
设抛物线的的解析式为y＝ax2+bx+c，把上面信息代入得，
，
解得，，
抛物线解析式为：，
把代入得，；
故答案为：

【思路引导】建立平面直角坐标系，再设抛物线的的解析式为y＝ax2+bx+c，再求出抛物线的解析式，然后将x=3.5代入计算即可。
39．（2021九上·温州月考）小刚家装有一种可调节淋浴喷头高度的淋浴器，完全开启后，水流近似呈抛物线状，升降器AB和淋浴喷头BC所成∠ABC＝135°，其中AB＝10cm，BC＝ cm.刚开始时，OA＝140cm，水流所在的抛物线恰好经过点A，抛物线落地点D和点O相距70cm.为了方便淋浴，淋浴器仍需完全处于开启的状态，且要求落地点和点O的距离增加10cm，则小刚应把升降器AB向上平移　 　cm.

【答案】60
【完整解答】解：过点C作 延长线于点E，





cm

以点O为原点，OA为y轴正方向，OD为x轴正方向，以1cm为一个单位，建立直角坐标系，
则 A(0，140)，C(20，150)，D(70，0)，D'(80，0)
设此时抛物线解析式为：
代入点 A(0，140)，C(20，150)，D(70，0) 得，
， 整理得，
解得

设小刚应把升降器向上平移kcm，即将抛物线向上平移k个单位，则抛物线解析式为：
将 代入解析式得，


即小刚应把升降器向上平移60cm.
故答案为：60.
【思路引导】过点C作CE⊥AB的延长线于点E，由邻补角的性质求出∠CBE的度数，进而得到BE、AE的值，以点O为原点，OA为y轴正方向，OD为x轴正方向，以1cm为一个单位，建立直角坐标系，可得点A、C、D、D′的坐标，利用待定系数法求出抛物线的解析式，设小刚应把升降器向上平移kcm，表示出平移后对应的抛物线解析式，然后将D′的坐标代入可得k，据此解答.
40．（2021九上·宜春期末）如图，人工喷泉有一个竖直的喷水枪AB，喷水口A距地面2.25m，喷泉水流的运动路线是抛物线，水流的最高点P到喷水枪AB所在直线的距离为1m，且到地面的距离为3m，以B点为原点，地面水平线和AB所在的直线为x，y轴建立平面直角坐标系，求水流的落地点C到水枪底部B的距离．

【答案】解：设抛物线的解析式为y=a(x−1) 2+3.
把A(0 ， 2.25)代入解得a=−0.75；
所以y=−0.75 (x−1) 2+3
当y=0时，−0.75 (x−1) 2+3=0
解得x1=−1（舍），x2=3
所以水流的落地点C到水枪底部B的距离为3m.
【思路引导】利用待定系数法求函数解析式即可。
41．（2020九上·海门月考）如图所示，公园要造圆形的喷水池，在水池中央垂直于水面处安装一个柱子OA，O恰在水面中心，OA=1.25m，由柱子顶端A处的喷头向外喷水，水流在各个方向沿形状相同的抛物线路线落下，为使水流形状较为漂亮，要求设计成水流在离OA距离为1m处达到距水面距离最大，高度2.25m.若不计其他因素，那么水池的半径至少要多少米才能使喷出的水流不致落到池外?

【答案】解：以地面上任一条直线为x轴，OA为y轴建立直角坐标系，
设y=a(x-1)2+2.25，则当x=0时，y=1.25，故a+2.25=1，a=-1.
由y=0得-(x-1)2+2.25=0，得(x-1)2=2.25，解得x1=2.5，x2=-0.5(舍去)
故水池的半径至少要2.5米.
【思路引导】以地面上任一条直线为x轴，OA为y轴建立直角坐标系，由题意可设y=a(x-1)2+2.25，再根据x=0时，y=1.25即可求得函数关系式，再求出抛物线与x轴的交点坐标即可得到结果.
42．（2021九上·全椒期末）某游乐场的圆形喷水池中心O有一雕塑OA，从A点向四周喷水，喷出的水柱为抛物线，且形状相同。如图，以水平方向为x轴，点O为原点建立直角坐标系，点A在y轴上，x轴上的点C、D为水柱的落水点，水柱所在抛物线(第一象限部分)的函数表达式为．

（1）求落水点C、D之间的距离；
（2）若需在OD上离O点10米的E处竖立雕塑EF，，且雕塑的顶部刚好碰到水柱，求雕塑EF的高．
【答案】（1）解：当y＝0时，，
解得：x1＝﹣1（舍去），x2＝11，
∴点D的坐标为（11，0），
∴OD＝11m．
∵从A点向四周喷水，喷出的水柱为抛物线，且形状相同，
∴OC＝OD＝11m，
∴CD＝OC+OD＝22m．
（2）解：∵，，
当x＝10时，，
∴点F（10，）
∴雕塑EF的高为米．
【思路引导】（1）令y=0，求出x的值，可得D（11，0），则OD=11m，由题意可得OC=OD=11m，然后根据CD=OC+OD进行计算；
（2）令x=10，求出y的值，可得点F的坐标，据此解答.
知识点06：二次函数的实际应用—百分率问题
43．（2018九上·营口期末）中国“一带一路”倡议给沿线国家和地区带来很大的经济效益，沿线某地区居民2016年年收入300美元，预计2018年年收入将达到1500美元，设2016年到2018年该地区居民年人均收入平均增长率为x，可列方程为（　　）
A．300（1+x）2＝1500 B．300（1+2x）＝1500
C．300（1+x2）＝1500 D．300+2x＝1500
【答案】A
【完整解答】设2016年到2018年该地区居民年人均收入平均增长率为x，
那么根据题意得2018年年收入为：300（1+x）2，
列出方程为：300（1+x）2=1500.
故答案为：A.
【思路引导】根据增长后的量=增长前的量×（1+增长率）增长次数可列方程.

44．（2021九上·大兴期中）某种商品的价格是 元，准备进行两次降价．如果每次降价的百分率都是 ，经过两次降价后的价格 （单位：元）随每次降价的百分率 的变化而变化，则 关于 的函数解析式是（　　）
A． B． C． D．
【答案】B
【完整解答】解：根据题意得y=2（1-x）2，
所以y与x之间的函数解析式为y=2（1-x）2．
故答案为：B.

【思路引导】根据“现价=原价×（1+百分率）”，即可得到y与x之间的函数解析式为y=2（1-x）2．
45．（2021九上·合肥月考）据省统计局公布的数据，合肥市2021年第一季度GDP总值约为2.4千亿元人民币，若我市第三季度GDP总值为y千亿元人民币，平均每个季度GDP增长的百分率为x，则y关于x的函数表达式是（　　）
A． B．
C． D．
【答案】C
【完整解答】解：已知平均每个季度 增长的百分率为 ，
则 关于 的函数表达式是： ．
故答案为：C．

【思路引导】根据“当前季度的GDP=前一个季度的GDP×（1+增长率）”可列出函数表达式。
46．（2021九上·宝山期末）据了解，某蔬菜种植基地2019年的蔬菜产量为100万吨，2021年的蔬菜产量为万吨，如果2019年至2021年蔬菜产量的年平均增长率为，那么y关于x的函数解析式为　 　．
【答案】
【完整解答】解：根据题意可得：2020年的蔬菜产量为，
2021年的蔬菜产量为，
∴，
故答案为： ．

【思路引导】 2019年至2021年 ，2019年蔬菜产量为100万吨，即可得出答案。
47．为解决民生问题，国家对某药品价格分两次降价，该药品的原价是48元，降价后的价格是30元，若平均每次降价的百分率均为x，可列方程为　 　 。
【答案】48(1-x)2=30
【完整解答】解：设平均的降价率为x，根据题意可知
48（1-x）2=30
【思路引导】根据题意，列出方程即可得到答案。
48．据权威部门发布的消息，2019年第一季度安徽省城镇居民人均可支配收入约为0.75万元，若第三季度安徽省城镇居民人均可支配收入为y万元，平均每个季度城镇居民人均可支配收入增长的百分率为x，则y与x之间的函数表达式是　 　 。
【答案】y=0.75(1+x)2
【完整解答】由题意可得： y与x之间的函数表达式是 y=0.75(1+x)2。
【思路引导】根据平均增长率问题的相等关系”增长前的量·（1+增长率）增长次数=增长后的量“写出关系式即为所求。
49．（2019九上·天台月考）某种药品原价为36元/盒，经过连续二次降价后售价为25元/盒，求平均每次降价的百分率。
【答案】解：设每次降价的百分率为x,
则36(1-x)2=25,
(1-x)2=,
∴1-x=±，
∴x=或x=-（舍）,
∴
【思路引导】设每次降价的百分率为x, 原价为36，第一次降价后为36（1-x）, 第二次降价后为36(1-x)2，再根据第二次降价后售价为25元/盒，列方程求出x即可.
50．（2020九上·沭阳期中）宿迁市为创建“文明城市”，积极投入资金进行河道治污与园林绿化两项工程，已知2018年投资1000万元，2020年预计投资1210万元.若这两年内平均每年投资增长的百分率相同.
（1）求平均每年投资增长的百分率；
（2）按此增长率，计算2021年投资额能否达到1360万？
【答案】（1）解：设平均每年投资增长的百分率为x，
1000(1+x)2=1210，
解得：x1=0.1，x2=－2.1（舍去），
增长率为10%.
答：平均每年投资增长的百分率为10%.
（2）解：不能达到1360，
∵1210×(1+10%)=1331＜1360，
∴不能.
答：2021年投资额不能达到1360万.
【思路引导】（1）设平均每年投资增长的百分率为x，则2019年投资1000(1+x)万元，2020年投资1000(1+x)2万元，再根据2020年预计投资1210万元列方程求解即可.（2）根据（1）求出的增长率计算出2021年投资额，判断能否到达1360万即可.