



【同步讲义】(苏教版2019)高中数学必修一:第17讲 三角函数的图像与性质 讲义
展开第17讲 三角函数的图像与性质
【知识梳理】
知识点一 周期函数
1.周期函数的定义
一般地,对于函数f(x),如果存在一个非零的常数T,使得定义域内的每一个x值 ,都满足f(x+T)=f(x),那么函数f(x)就叫做周期函数,非零常数T叫做这个函数的周期.
2.最小正周期
对于一个周期函数f(x),如果在它所有的周期中存在一个最小的正数,那么这个最小的正数就叫做f(x)的最小正周期.
知识点二 正弦函数、余弦函数、正切函数的周期
1.正弦函数、余弦函数的周期
正弦函数和余弦函数都是周期函数,2kπ(k∈Z且k≠0)都是它们的周期,它们的最小正周期都是2π.
2.正切函数的周期
正切函数是周期函数,最小正周期是π.
3.函数y=Asin(ωx+φ)和y=Acos(ωx+φ)的周期
一般地,函数y=Asin(ωx+φ)和y=Acos(ωx+φ)(其中A,ω,φ为常数,且A≠0,ω>0)的周期T=.
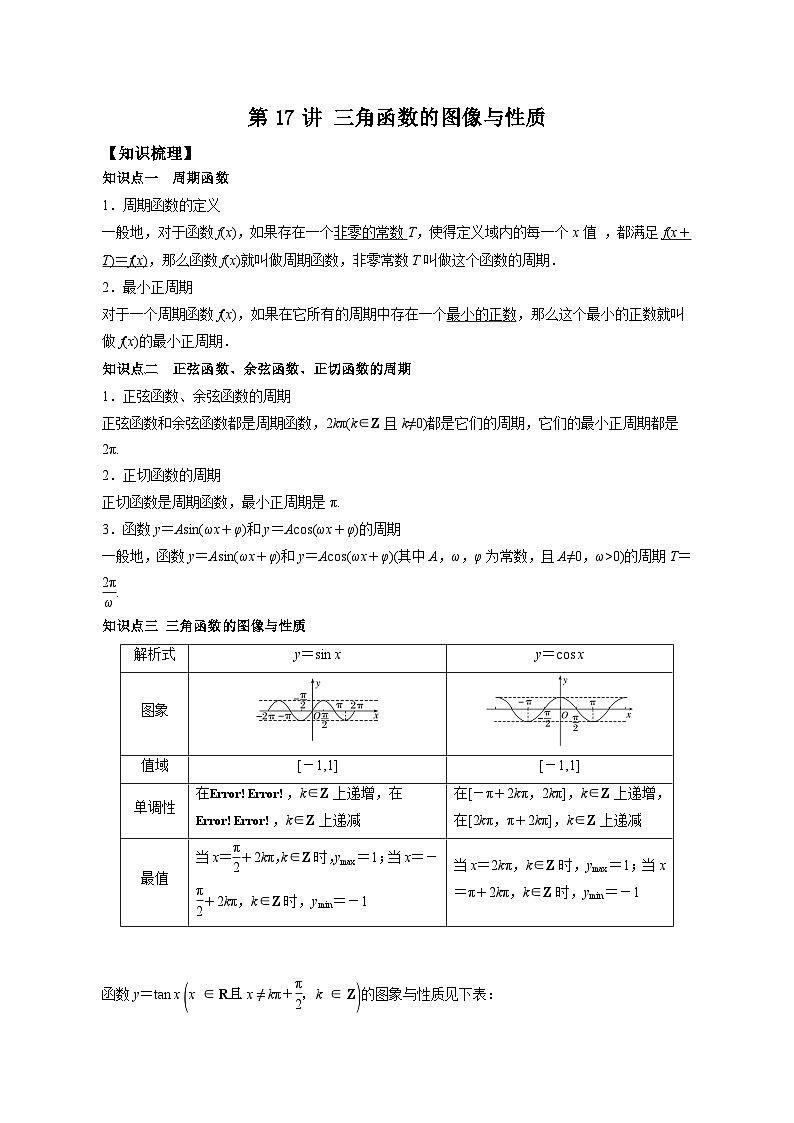
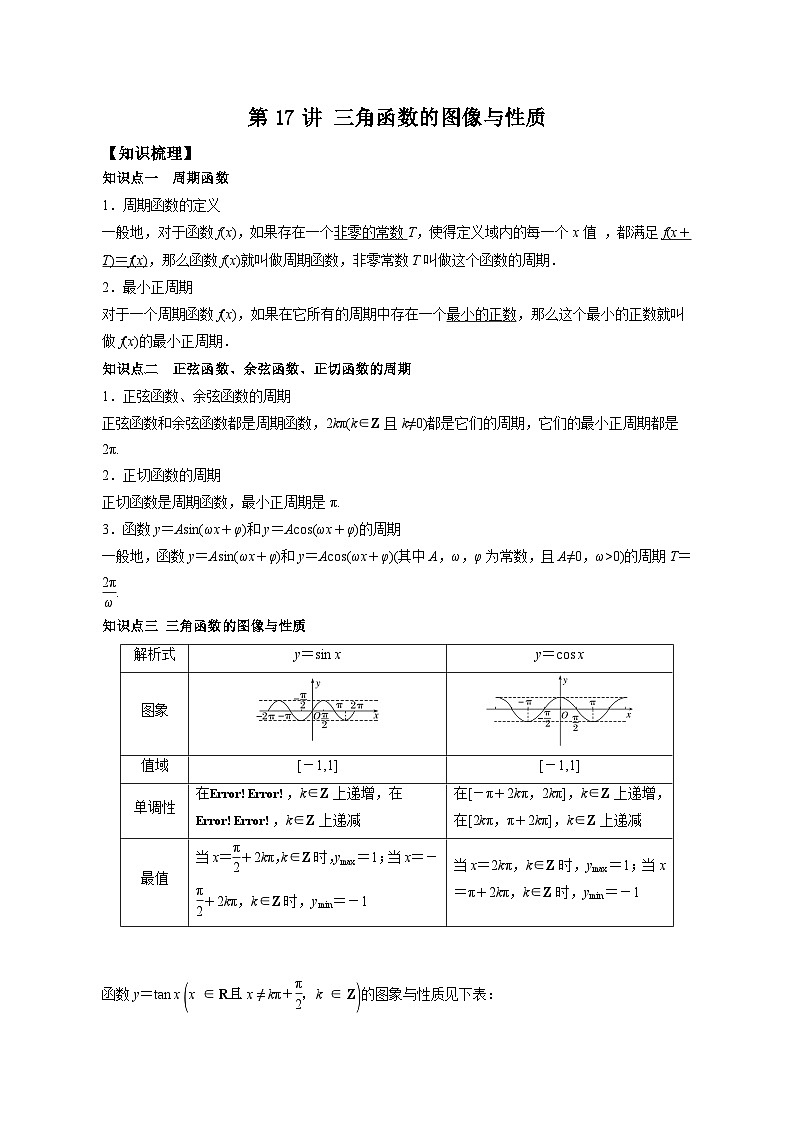
知识点三 三角函数的图像与性质
解析式 | y=sin x | y=cos x |
图象 | ||
值域 | [-1,1] | [-1,1] |
单调性 | 在,k∈Z上递增,在,k∈Z上递减 | 在[-π+2kπ,2kπ],k∈Z上递增, 在[2kπ,π+2kπ],k∈Z上递减 |
最值 | 当x=+2kπ,k∈Z时,ymax=1;当x=-+2kπ,k∈Z时,ymin=-1 | 当x=2kπ,k∈Z时,ymax=1;当x=π+2kπ,k∈Z时,ymin=-1 |
函数y=tan x的图象与性质见下表:
解析式 | y=tan x |
图象 | |
定义域 | |
值域 | R |
最小正周期 | π |
奇偶性 | 奇 |
单调性 | 在开区间(k∈Z)内都是增函数 |
知识点四 图像平移
如图所示,对于函数y=sin(x+φ)(φ≠0)的图象,可以看作是把y=sin x的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平行移动|φ|个单位长度而得到的.
如图所示,函数y=sin(ωx+φ)(ω>0)的图象,可以看作是把y=sin(x+φ)的图象上所有点的横坐标缩短(当ω>1时)或伸长(当0<ω<1时)到原来的倍(纵坐标不变)而得到.
如图所示,函数y=Asin(ωx+φ)(A>0,ω>0)的图象,可以看作是把y=sin(ωx+φ)图象上所有点的纵坐标伸长(当A>1时)或缩短(当0<A<1时)到原来的A倍(横坐标不变)而得到.
知识点五 函数y=Asin(ωx+φ),A>0,ω>0中参数的物理意义
【典型例题】
考点一:函数的周期性
- 设为定义在上的奇函数,且满足,,则
A. B. C. D.
- 已知定义在上的奇函数满足当时,,则下列结论正确的是( )
A. 的图象关于轴对称 B.
C. D.
- 定义在上的函数的图象关于点成中心对称,对任意的实数都有,且,,则的值为( )
- B. C. D.
考点二:函数的值域
- 函数的值域是( )
A. B. C. D. 以上均不对
- 已知函数定义域为,值域为,则 .
考点三:函数的单调性
- 已知函数
求函数的单调递增区间
若,,求函数的最值.
- 函数为增函数的区间是 .
考点四:三角函数的性质
- 已知函数,则下列说法正确的是( )
A. 的图象关于直线对称 B. 是图象的一个对称中心
C. 的周期为 D. 在区间单调递减
- 设函数,则下列结论错误的是( )
- 的一个周期为 B. 的图象关于直线对称
C. 的一个零点为 D. 在单调递减
考点五:图像与性质
- 已知函数在一个周期内的图象如图所示,其中图象最高点、最低点的横坐标分别为、,图象在轴上的截距为则下列结论正确的是( )
- 的最小正周期为 B. 的最大值为
C. 在区间上单调递增 D. 为偶函数
考点六:平移
- 已知曲线:,:,则下面结论正确的是( )
A. 把上各点的横坐标伸长到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线
B. 把上各点的横坐标伸长到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线
C. 把上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线
D. 把上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线
- 已知函数是奇函数,将的图象上所有点的横坐标伸长到原来的倍纵坐标不变,所得图象对应的函数为若的最小正周期为,且,则( )
- B. C. D.
考点七:零点问题
- 函数,的图象与直线为常数的交点可能有( )
A. 个 B. 个 C. 个 D. 个
- 已知,函数在区间内仅有一个零点,则的取值范围是
- 设函数,已知在上有且仅有个零点,则( )
A. 的取值范围是
B. 的图象与直线在上的交点恰有个
C. 的图象与直线在上的交点恰有个
D. 在上单调递减
- 已知函数的图像过点,最小正周期为,且最小值为.
求函数的解析式
若,的值域是,求的取值范围.
- 已知函数的部分图象如图所示.
求,和的值;
求函数在上的单调递减区间;
若函数在区间上恰有个零点,求的取值范围.
考点八:恒成立问题
- 已知函数的部分图象如图所示。
求函数的解析式
将函数图象上每个点的横坐标变为原来的倍纵坐标不变,再将得到的图象向右平移个单位长度,所得图象的函数为,若不等式在恒成立,求实数的取值范围。
考点九:奇偶性
- 若将函数的图象向左平移个单位后,所得图象对应的函数为偶函数,则的最小值是 .
- 有以下四个命题,正确命题的是( )
A. 若函数为奇函数,则为的整数倍
B. 若函数为奇函数,则为的整数倍
C. 对于函数,若,则必是的整数倍
D. 对于函数,若,则必是的整数倍
- 已知函数的最小正周期为.
求当为偶函数时的值;
若的图象过点,求的单调递增区间.
高中数学苏教版 (2019)必修 第一册7.1 角与弧度优秀同步达标检测题: 这是一份高中数学苏教版 (2019)必修 第一册7.1 角与弧度优秀同步达标检测题,文件包含第15讲角与弧度原卷版docx、第15讲角与弧度解析版docx等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。
苏教版 (2019)必修 第一册4.1 指数优秀课后测评: 这是一份苏教版 (2019)必修 第一册4.1 指数优秀课后测评,文件包含第13讲指数函数原卷版docx、第13讲指数函数解析版docx等2份试卷配套教学资源,其中试卷共40页, 欢迎下载使用。
高中数学苏教版 (2019)必修 第一册6.1 幂函数优秀同步练习题: 这是一份高中数学苏教版 (2019)必修 第一册6.1 幂函数优秀同步练习题,文件包含第12讲幂函数原卷版docx、第12讲幂函数解析版docx等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。













