初中数学人教版九年级上册24.1.1 圆学案

这是一份初中数学人教版九年级上册24.1.1 圆学案，文件包含九年级数学上册第20讲圆中阴影部分面积计算技巧原卷版-2022-2023学年九年级数学上册常考点数学思想+解题技巧+专项突破+精准提升docx、九年级数学上册第20讲圆中阴影部分面积计算技巧解析版-2022-2023学年九年级数学上册常考点数学思想+解题技巧+专项突破+精准提升docx等2份学案配套教学资源，其中学案共47页， 欢迎下载使用。
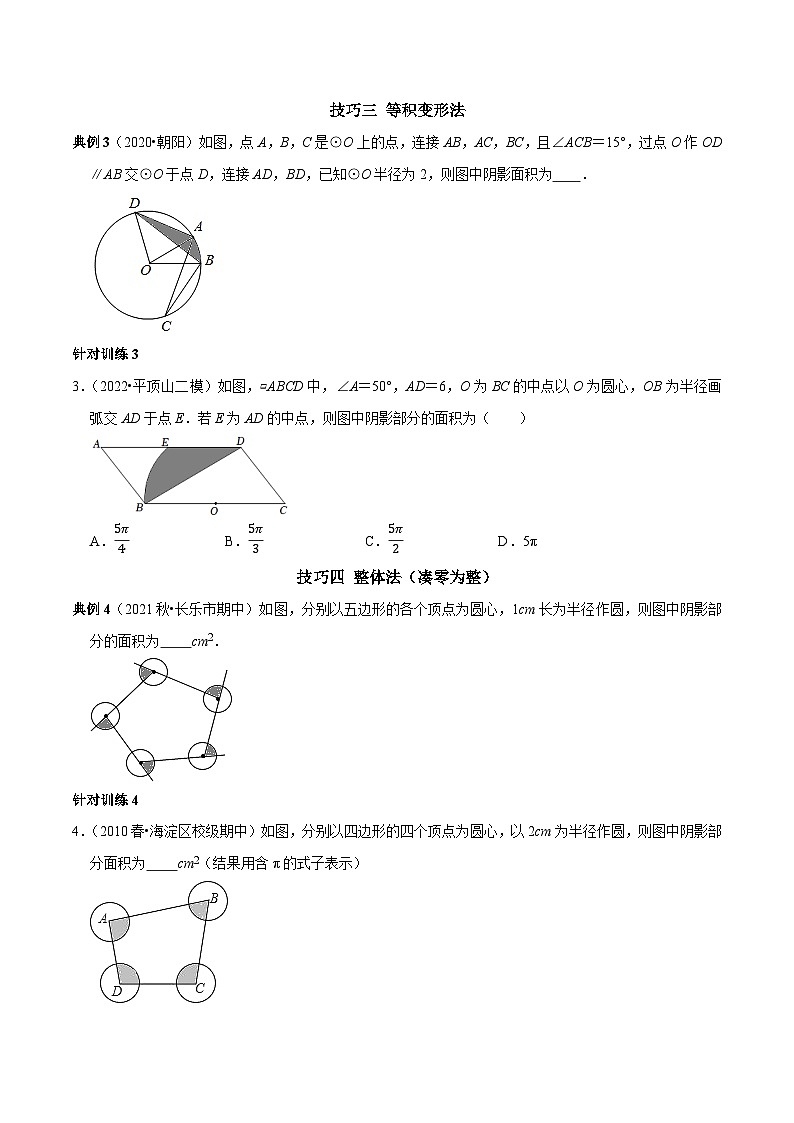
第20讲   圆中阴影部分面积计算技巧（解析版）第一部分   典例剖析+针对训练技巧一 公式法典例1（2022•枝江市一模）如图，从一块直径为4dm的圆形铁皮上剪出一圆心角为90°的扇形，则此扇形的面积为（　　）dm2．A．4π B．16π C．4π D．8π针对训练11．（2020•呼和浩特）如图，△ABC中，D为BC的中点，以D为圆心，BD长为半径画一弧，交AC于点E，若∠A＝60°，∠ABC＝100°，BC＝4，则扇形BDE的面积为       ．技巧二 和差法典例2（2020•苏州）如图，在扇形OAB中，已知∠AOB＝90°，OA，过的中点C作CD⊥OA，CE⊥OB，垂足分别为D、E，则图中阴影部分的面积为（　　）A．π﹣1      B．1    C．π        D．针对训练22．（2022•紫金县二模）如图，已知平行四边形ABCD，以B为圆心，AB为半径作交BC于E，然后以C为圆心，CE为半径作交CD于F，若AD＝5，FD＝3，∠B＝60°，则阴影部分的面积为（　　）A．π          B．3π         C．π            D．12π技巧三 等积变形法典例3（2020•朝阳）如图，点A，B，C是⊙O上的点，连接AB，AC，BC，且∠ACB＝15°，过点O作OD∥AB交⊙O于点D，连接AD，BD，已知⊙O半径为2，则图中阴影面积为　　．针对训练33．（2022•平顶山二模）如图，▱ABCD中，∠A＝50°，AD＝6，O为BC的中点以O为圆心，OB为半径画弧交AD于点E．若E为AD的中点，则图中阴影部分的面积为（　　）A． B． C． D．5π技巧四 整体法（凑零为整）典例4（2021秋•长乐市期中）如图，分别以五边形的各个顶点为圆心，1cm长为半径作圆，则图中阴影部分的面积为　 　cm2．针对训练44．（2010春•海淀区校级期中）如图，分别以四边形的四个顶点为圆心，以2cm为半径作圆，则图中阴影部分面积为　 　cm2（结果用含π的式子表示）技巧五 割补法典例5（2020•十堰）如图，圆心角为90°的扇形ACB内，以BC为直径作半圆，连接AB．若阴影部分的面积为（π﹣1），则AC＝　 　．针对训练55．（2020•贵港）如图，在扇形OAB中，点C在上，∠AOB＝90°，∠ABC＝30°，AD⊥BC于点D，连接AC，若OA＝2，则图中阴影部分的面积为　 　．技巧六 图形变化法典例6（2020•乐山）在△ABC中，已知∠ABC＝90°，∠BAC＝30°，BC＝1．如图所示，将△ABC绕点A按逆时针方向旋转90°后得到△AB′C′．则图中阴影部分面积为（　　）A． B． C． D．π针对训练66．（2020•黔东南州）如图，正方形ABCD的边长为2，O为对角线的交点，点E、F分别为BC、AD的中点．以C为圆心，2为半径作圆弧，再分别以E、F为圆心，1为半径作圆弧、，则图中阴影部分的面积为（　　）A．π﹣1 B．π﹣2 C．π﹣3 D．4﹣π7．（2019•招远市一模）如图，CD是⊙O的直径，AB是⊙O的弦，AB⊥CD，垂足为G，OG：OC＝3：5，AB＝8．点E为圆上一点，∠ECD＝15°，将沿弦CE翻折，交CD于点F，图中阴影部分的面积＝　　．类型七 重叠求余法典例7（2021•越秀区校级开学）如图，直径AB＝6的半圆，绕B点顺时针旋转30°，此时点A到了点A′，则图中阴影部分的面积是　 　．针对训练78．（2014秋•营口期末）如图，直径AB＝6的半圆，绕B点顺时针旋转60°，此时点A就到了点A′，则图中阴影部分的面积是　   ．
第二部分 专题提优训练1．（2022•赤峰）如图，AB是⊙O的直径，将弦AC绕点A顺时针旋转30°得到AD，此时点C的对应点D落在AB上，延长CD，交⊙O于点E，若CE＝4，则图中阴影部分的面积为（　　）A．2π B．2 C．2π﹣4 D．2π﹣22．（2022•运城二模）如图，将Rt△CAB绕点B按逆时针方向旋转90°后，得到Rt△A′BC′，已知∠BAC＝90°，∠ABC＝60°，BC＝2，则图中阴影部分面积为（　　）A．π B．π C．π D．π3．（2022•兴庆区校级一模）如图，在半圆O中，AB是半圆O的直径，AB＝4，OC⊥AB，连接BC，以BC为直径作半圆，则图中阴影部分的面积为（　　）A．1 B． C．2 D．π4．（2022•虞城县三模）如图，等腰三角形ABC中，∠BAC＝120°，AB＝AC＝2，以点B为圆心，以AB的长为半径作弧交BC于点D，过点D作DE∥AC交AB于点E，则图中阴影部分的面积为（　　）A． B． C． D．5．（2022•山西模拟）如图，正方形OCDE的边长为1，以点O为圆心，对角线OD为半径画弧分别交OC，OE的延长线于点A、B，过点A作AF∥OB交ED的延长线于点F．则图中阴影部分的面积为（　　）A． B． C． D．6．（2022•山西）如图，扇形纸片AOB的半径为3，沿AB折叠扇形纸片，点O恰好落在上的点C处，图中阴影部分的面积为（　　）A．3π﹣3 B．3π C．2π﹣3 D．6π7．（2022•李沧区二模）如图，在Rt△ABC中，∠ABC＝90°，AB＝4，BC＝4，以AB的中点O为圆心，OA的长为半径作圆，交AC于点D，则图中阴影部分的面积为（　　）A． B． C． D．8．（2022•上蔡县模拟）如图，在扇形OBA中，∠AOB＝120°，OA＝2，点C，D分别是线段OB和AB的中点，连接CD，交AB于点E，则图中阴影部分的面积为 　   　．9．（2022•启东市二模）如图，以AB为直径的半圆O，绕点A顺时针旋转45°，点B的对应点为点C，AC交半圆O于点D，若，则图中阴影部分的面积为 　    　．10．（2022•河南）如图，将扇形AOB沿OB方向平移，使点O移到OB的中点O′处，得到扇形A′O′B′．若∠O＝90°，OA＝2，则阴影部分的面积为 　    　．11．如图，在平行四边形ABCD中，∠BAC＝90°，BC＝4，∠BCA＝30°，E为AD上一点，以点A为圆心，AE长为半径画弧，交BC于点F，若BF＝AB，则图中阴影部分的面积为 　  　（结果保留π）．12．（2022•梁园区）如图，在⊙O中，OA⊥OB，CD＝DE，∠CDE＝90°，则图中阴影部分的面积为 　　．13．（2022•朝阳区一模）如图，在平行四边形ABCD中，∠BAC＝60°，∠ABC＝100°，BC＝6，点E为BC的中点，以点E为圆心，线段BE的长为半径画弧，交AC于点F，则阴影部分的面积为 　π　．（结果保留π）14．（2022•兰山区二模）正方形ABCD中，点⊙O为对角线的交点，以点C为圆心，以OC为半径作弧，交BC于点F，交CD于点G，以点D为圆心，以AD为半径作弧，交BD于点E，若AB＝1，则阴影部分的面积为 　　．15．（2022•安阳一模）如图，菱形纸片ABCD的边长为6，∠A＝60°，在菱形中剪下一个以点A为圆心，AB长为半径的扇形后，在剩余部分中再剪下一个圆，若以剪下的扇形为侧面，以剪下的圆形为底面，恰好可以围成一个圆锥的表面，则纸片剩下部分的面积为 　    　． 16．（2022•南召县模拟）在矩形ABCD中，，BC＝2，以A为圆心，AD为半径画弧交线段BC于E，连接AE，则阴影部分的面积为 　  　．17．（2022•北碚区校级模拟）如图，矩形ABCD中，以A为圆心，AB的长为半径画圆，交CD于点E，再以D为圆心，DA的长为半径画圆，恰好经过点E．已知AB＝2，AD＝2，则图中阴影部分的面积为 　 　．18．（2022•禄劝县二模）如图，在正方形ABCD中，AB＝2，对角线AC，BD交于点O．则图中阴影部分的面积为 　     　．19．（2022•佛山校级三模）如图，在▱ABCD中，AB＝2，以点C为圆心，CD长为半径画弧，与BC，AD分别交于点E，F，过点F作FG⊥BC于点G，若FG，则图中阴影部分的面积为 　   　．20．（2022•郧西县模拟）如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作DF⊥AC，垂足为点F，若⊙O的半径为，∠CDF＝15°，则阴影部分的面积为 　　．21．（2022•南京二模）如图，在矩形ABCD中，AD＝1，AB，以点A为圆心，AB长为半径画弧交CD于点E，则阴影部分的面积为      　．
22．（2019秋•玄武区期末）如图，AB是⊙O的弦，AB＝4，点P在上运动（点P不与点A、B重合），且∠APB＝30°，设图中阴影部分的面积为y．（1）⊙O的半径为　 　；（2）若点P到直线AB的距离为x，求y关于x的函数表达式，并直接写出自变量x的取值范围．