高中数学人教A版 (2019)选择性必修 第三册第六章 计数原理6.3 二项式定理优秀练习

这是一份高中数学人教A版 (2019)选择性必修 第三册第六章 计数原理6.3 二项式定理优秀练习，文件包含631二项式定理+632二项式系数的性质精讲原卷版docx、631二项式定理+632二项式系数的性质精讲解析版docx等2份试卷配套教学资源，其中试卷共42页， 欢迎下载使用。
6.3.1二项式定理+6.3.2二项式系数的性质 (精讲）
目录
一、必备知识分层透析
二、重点题型分类研究
题型1：求型的展开式
题型2：二项展开式的逆用
题型3：二项展开式中的特定项或特定系数问题
题型4：三项展开式中的特定项或特定系数问题
题型5：几个二项式的和或积的展开式中的特定项或特定系数问题
题型6：系数最大项问题
题型7：赋值法解决系数和问题
题型8：有关整除或求余问题
三、高考（模拟）题体验
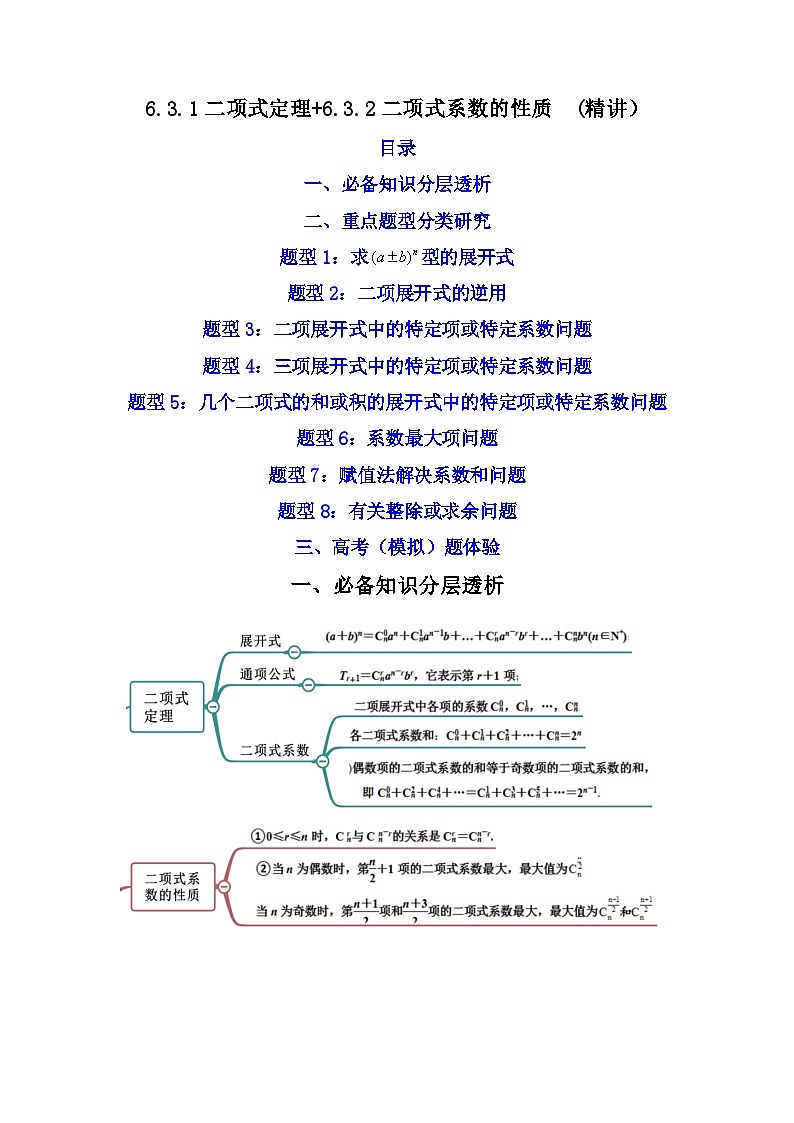
一、必备知识分层透析




知识点1：知识链接
（1）
（2）
知识点2：二项式定理及相关概念
（1）二项式定理
一般地，对于每个（），的展开式中共有个，将它们合并同类项，就可以得到二项展开式：（）.这个公式叫做二项式定理.
（2）二项展开式
公式中：，等号右边的多项式叫做的二项展开式.
（3）二项式系数与项的系数
二项展开式中各项的二项式系数为(),项的系数是指该项中除变量外的常数部分,包含符号等.
（4）二项式定理的三种常见变形
①
②
③
知识点3：二项展开式的通项
二项展开式中的()叫做二项展开式的通项,用表示,即通项为展开式的第项:.通项体现了二项展开式的项数、系数、次数的变化规律,是二项式定理的核心,它在求展开式的某些特定项(如含指定幂的项常数项、中间项、有理项、系数最大的项等)及其系数等方面有着广泛的应用.
知识点4：二项式展开式中的最值问题
（1）二项式系数的性质
①每一行两端都是，即；其余每个数都等于它“肩上”两个数的和，即．
②对称性每一行中，与首末两端“等距离”的两个二项式系数相等，即．
③增减性：当时，二项式系数递增，当时，二项式系数递减；
④二项式系数和令，则二项式系数的和为，变形式．
⑤奇数项的二项式系数和等于偶数项的二项式系数和在二项式定理中，令，
则，从而得到：．
⑥最大值：如果二项式的幂指数是偶数，则中间一项的二项式系数最大；
如果二项式的幂指数是奇数，则中间两项，的二项式系数，相等且最大．
（2）系数的最大项
求展开式中最大的项，一般采用待定系数法．设展开式中各项系数分别为，设第项系数最大，应有，从而解出来．
知识点5：二项式展开式中系数和有关问题
常用赋值举例：
（1）设，
二项式定理是一个恒等式，即对，的一切值都成立，我们可以根据具体问题的需要灵活选取，的值．
①令，可得：
②令，可得：，即：
（假设为偶数），再结合①可得：
．
（2）若，则
①常数项：令，得．
②各项系数和：令，得．
③奇数项的系数和与偶数项的系数和
（i）当为偶数时，奇数项的系数和为；
偶数项的系数和为．
（可简记为：为偶数，奇数项的系数和用“中点公式”，奇偶交错搭配）
（ii）当为奇数时，奇数项的系数和为；
偶数项的系数和为．
（可简记为：为奇数，偶数项的系数和用“中点公式”，奇偶交错搭配）
若，同理可得．
注意：常见的赋值为令，或，然后通过加减运算即可得到相应的结果．
二、重点题型分类研究
题型1：求型的展开式
典型例题
例题1．（2023·全国·高三专题练习）下列不属于的展开式的项的是（    ）
A． B． C． D．
【答案】B
【详解】由二项式定理可知，，故不是展开式的项.
故选：B
例题2．（2022·高二课时练习）求的展开式．
【答案】.
【详解】．
例题3．（2022·高二课时练习）求的展开式．
【答案】
【详解】解：根据二项式定理，


所以
同类题型演练
1．（2022·高二课时练习）求展开式的各项系数．
【答案】
【详解】因为，
故展开式的各项系数为：.
2．（2022·高二课时练习）求的展开式．
【答案】
【详解】
3．（2022·高二课时练习）求的展开式．
【答案】
【详解】对，不妨令，
故
.
故求的展开式为：.
题型2：二项展开式的逆用
典型例题
例题1．（2022·全国·高三专题练习）已知，则（    ）
A．31 B．32 C．15 D．16
【答案】A
【详解】逆用二项式定理得，即，所以n=5，所以．
故选:A
例题2．（2022·全国·高三专题练习）若，则（    ）
A． B． C． D．
【答案】B
【详解】

.
故选：B
例题3．（2022·全国·高三专题练习）__________.
【答案】1
【详解】因为，
所以，
故答案为：1
同类题型演练
1．（2022·高二课时练习）已知，则可化简为（    ）
A． B． C． D．
【答案】A
【详解】,
故选：A.
2．（2022·高二课时练习）(x－1)5＋5(x－1)4＋10(x－1)3＋10(x－1)2＋5(x－1)＝
A．x5 B．x5－1
C．x5＋1 D．(x－1)5－1
【答案】B
【详解】逆用二项式定理，得原式＝[(x－1)＋1]5－1＝x5－1.
故选B.
3．（2022·高二课时练习）·2n＋·2n－1＋…＋·2n－k＋…＋＝________.
【答案】3n
【详解】由二项式的展开式定理可得：原式＝(2＋1)n＝3n.
故答案为：3n.
4．（2022·高二课时练习）计算：_____.
【答案】
【详解】由题得原式=.
故答案为：
题型3：二项展开式中的特定项或特定系数问题
典型例题
例题1．（2023·全国·高三专题练习）已知的展开式中含的项的系数为（    ）
A．30 B．-30 C．25 D．-25
【答案】A
【详解】展开式的第项为，令，得，故展开式中含的项的系数为．
故选：A．
例题2．（2023·北京·高三专题练习）二项式的展开式中常数项为（    ）
A．80 B． C． D．40
【答案】B
【详解】解：二项式的展开式的通项为，
令，则，
所以常数项为.
故选：B.
例题3．（2022秋·湖北黄石·高二校考期中）已知的展开式中，常数项为135，则的值为（    ）
A．3 B． C．2 D．3，
【答案】D
【详解】展开式的通项为，
令，可得，因此，展开式中的常数项为.
则，.
故选：D.
例题4．（2023·全国·高三专题练习）在二项式 的展开式中， 系数为有理数的项的个数是_____.
【答案】6
【详解】二项展开式的通项公式为，
第项的系数为，
当即时，系数为有理数，
这样的项的个数为6，
故答案为：6
例题5．（2022秋·上海浦东新·高二上海市建平中学校考期末）若展开式中的系数为，则实数的值为___________.
【答案】或
【详解】展开式通项为：
令，则，解得：.
故答案为：.
同类题型演练
1．（2023·全国·高三专题练习）展开式中的常数项为（    ）
A． B． C． D．
【答案】B
【详解】展开式中的常数项为.
故选：B.
2．（2023·四川成都·统考二模）二项式展开式中的系数为（    ）
A．120 B．135 C．140 D．100
【答案】B
【详解】的展开式通项公式为，
其中，，，
故二项式中的四次方项为，
即展开式中的系数为.
故选：B
3．（2023·全国·高三专题练习）的展开式中的常数项为__________.
【答案】
【详解】解：的展开式的通项为，
令，则，
所以的展开式中的常数项为.
故答案为：.
4．（2023·高二单元测试）在的二项展开式中，的系数为______．
【答案】##2.5
【详解】因为展开式的通项为
令，可得的系数为.
故答案为：.
5．（2022秋·甘肃临夏·高二统考期末）若的展开式中含项的系数为-32，则______．
【答案】-2
【详解】因为的展开式的通项公式为，
故的展开式中含项的系数为，
整理得，所以,
故答案为：
题型4：三项展开式中的特定项或特定系数问题
典型例题
例题1．（2023·全国·高三专题练习）的展开式中的系数为（    ）
A．4 B．6 C．8 D．12
【答案】B
【详解】的通项公式，
令，则，
所以的系数为，
故选：B
例题2．（2023·全国·高三专题练习）若的展开式中的系数为35，则正数（    ）
A． B．2 C． D．4
【答案】B
【详解】因为展开式为：，
即
，
所以，
，
，
所以含的系数为，又为正数，所以.
故选：B.
例题3．（2023·全国·高三专题练习）在的二项展开式中含项的系数为______
【答案】21
【详解】的展开式的通项为．
的展开式的通项为．
由，得，
，，或，
在的展开式中，
含项的系数为．
故答案为：21
例题4．（2023·全国·高三专题练习）的展开式中，含项的系数为______.
【答案】
【详解】展开式的通项为，
令，则展开式中含的项为，
所以含项的系数为.
同类题型演练
1．（2023·全国·高三专题练习）的展开式中，项的系数为（    ）
A．400 B．480 C．720 D．800
【答案】D
【详解】，
的展开式通项为，的展开式通项为，
所以的展开式通项为，
其中，，且、，
令，可得或或，
因此的展开式中的系数为.
故选：D.
2．（2023·全国·高三专题练习）的展开式中，的系数为（    ）
A． B． C． D．
【答案】D
【详解】可看作5个因式相乘，
所以其展开式中含的项为4个因式取，2个因式取，
所以展开式中含的系数为．
故选：D．
3．（2023·全国·高三专题练习）在的展开式中，含项的系数为（    ）
A． B．480 C． D．240
【答案】A
【详解】看成是6个相乘，要得到.分以下情况:
6个因式中，2个因式取，1个因式取，3个因式取，此时的系数，所以的系数为.
故选：A
4．（2023·全国·高三专题练习）的展开式中常数项为______
【答案】
【详解】将原式看成6个相同的因子相乘，按x的选取个数分类，
得展开式中常数项为．
故答案为：-59
题型5：几个二项式的和或积的展开式中的特定项或特定系数问题
典型例题
例题1．（2023春·江西·高三校联考阶段练习）在的展开式中常数项为（    ）
A．14 B．－14 C．6 D．－6
【答案】D
【详解】由二项式定理得，
所以所求常数项为．
故选：D．
例题2．（2023·全国·高三专题练习）的展开式中含的项的系数为（    ）
A．10 B．15 C．20 D．25
【答案】B
【详解】的展开式的通项为，
则的展开式中含的项是，
所以的展开式中含的项的系数为15.
故选：B
例题3．（2023·全国·高三专题练习）展开式中的系数为___（用数字作答）．
【答案】
【详解】因为的展开式通项为，
，
在中，，在中，令，可得，
所以，展开式中的系数为.
故答案为：.
例题4．（2023·全国·高三专题练习）在展开式中，的系数为________.
【答案】7
【详解】化简得，根据该展开式的通项公式，可得
，则的系数为7.
故答案为：7
同类题型演练
1．（2023·全国·高三专题练习）已知的展开式中各项系数之和为，则该展开式中含的项的系数为（    ）
A． B． C． D．
【答案】D
【详解】令得，，解得，所以的展开式中含的项的系数为．
故选：D.
2．（2023·全国·高三专题练习）的展开式中的系数为（    ）
A． B．60 C．12 D．
【答案】D
【详解】因为的展开式的通项：，
令，或，解得，（舍去），
所以的展开式中的系数为,
故选：D
3．（2023·全国·高三专题练习）的展开式中的系数为_______________.
【答案】40
【详解】因为的展开式的通项，
令和，可得的系数为.
故答案为：40.
4．（2023·全国·模拟预测）在的展开式中，x2y5项的系数是___________.
【答案】-12
【详解】解：的通项为，
令此时，
令此时，
所以展开式中，x2y5项的系数是.
故答案为：-12
题型6：系数最大项问题
典型例题
例题1．（2023·全国·高三专题练习）在展开式中，下列说法错误的是（    ）
A．常数项为 B．第5项的系数最大
C．第4项的二项式系数最大 D．所有项的系数和为1
【答案】B
【详解】展开式的通项为，
由，得，所以常数项为，A正确；
由通项公式可得为偶数时，系数才有可能取到最大值，
由，可知第项的系数最大，B错误；
展开式共有项，所以第项二项式系数最大，C正确；
令，得，所有项的系数和为，D正确；
故选：B.
例题2．（2023·高二课时练习）已知在的二项展开式中，第5项的系数与第3项的系数之比为10：1，求该二项展开式中系数最大的项的系数．
【答案】
【详解】解：由依题意，第5项的系数为，第3项的系数为，
则，解得．
设该二项展开式中第项的系数最大，
则，解得．
所以，第6项和第7项的系数相等且最大，
即所求系数最大的项的系数为．
例题3．（2023·全国·高三专题练习）若展开式中前三项的系数成等差数列，求：
(1)展开式中项的系数；
(2)展开式中系数最大的项．
【答案】(1)
(2)或
（1）解：前三项的系数为：，，，
故有，
即解得或（舍去）；
则二项式展开式的通式为．
令，解得，所以，故展开式中项的系数为．
（2）解：不妨设展开式中项的系数最大，则，
即，解得，即或，
故展开式中系数最大的项为，．
例题4．（2022春·辽宁沈阳·高二沈阳市第一二〇中学校考阶段练习）已知在的展开式中，前3项的系数分别为，且满足.求：
(1)展开式中二项式系数最大项的项；
(2)展开式中系数最大的项；
(3)展开式中所有有理项.
【答案】(1)
(2)和
(3)和
【详解】（1）因为展开式的通项公式为，，
所以
依题意得，即，由已知,
所以，
所以的展开式有9项，二项式系数最大的项为第5项，
所以.
（2）由（1）知，，
设展开式中系数最大的项为第项，则，
即，即，
解得，所以或，
所以展开式中系数最大的项为和.
（3）由为有理项知，为整数，得，，所以展开式中所有有理项为和.
同类题型演练
1．（2023·全国·高三专题练习）已知的展开式中各项系数之和等于的展开式的常数项，而的展开式中系数最大的项等于54，则正数的值为__________.
【答案】
【详解】展开式的通项为:
，
令，解得，故展开式的常数项为．
由题意可得，故有．
由于展开式的系数最大的项等于，，解得．
由于，所以
故答案为：
2．（2023·高二课时练习）已知在的二项展开式中，各项的系数之和比各项的二项式系数之和大992，求该二项展开式中系数最大的项．
【答案】
【详解】解：令，得各项的系数之和为，
而各项的二项式系数之和为，
则，得，解得或（舍去），
所以．
设该二项展开式中第项的系数最大，
则，得，解得，
又，于是．
所以所求系数最大的项是．
3．（2022春·福建福州·高二福建省福州格致中学校考阶段练习）已知的展开式中，二项式系数和为256.
(1)此展开式中有没有常数项？有理项的个数是几个？并说明理由；
(2)展开式中系数最大的项是第几项，并说明理由：
【答案】(1)此展开式中没有常数项；有理项有5个.
(2)展开式中系数最大的项是第6项和第7项.
【详解】（1）因为二项式系数和为，
所以.
原二项式展开式的通项为.
令，得，
故此展开式中没有常数项.
当时，可取，
故有理项有5个.
（2）由（1）得展开式中系数的通项为，
当时，递增；当时，递减.
同时在递增.
故前4项均不可能为最大.
当时，；
当时，；
当时，；
当时，；
当时，；
故当或时，展开式中对应项的系数最大，为.
即展开式中系数最大的项是第6项和第7项.
4．（2022春·河南南阳·高二校考阶段练习）在的展开式中，前三项的二项式系数之和等于79.
(1)求的值；
(2)若展开式中的常数项为，试问展开式中系数最大的项是第几项？
【答案】(1)
(2)第9项
【详解】（1）因为前三项的二项式系数之和等于79，
所以有，
解得或.
因为，所以.
（2）的通项为，
所以当，即时，常数项为，解得.
由不等式组解得.
因为，所以，所以展开式中系数最大的项是第9项.
题型7：赋值法解决系数和问题
典型例题
例题1．（2022·全国·高三专题练习）已知
(1)求；
(2)求.
【答案】(1)255
(2)32895

（1）
令，则.
令，则，①
故.
（2）
令，则，②
①+②可得，
故.
例题2．（2022·高二单元测试）从①第5项的系数与第3项的系数之比是7：6，②第2项与倒数第3项的二项式系数之和为55这两个条件中任选一个，补充在下面横线处上，解决下面两个问题.
已知，且的二项展开式中，______.
(1)求的值；
(2)求的值.
【答案】(1)选择①，；选择②，
(2)
（1）
的二项展开式的通项为.
选择①，由题意可知，整理得，解得或（舍去）.
选择②，由题意可知，整理得，解得或（舍去）.
（2）
由（1）知，则，
则，，，，，大于零，，，，，小于零.
令，得，令，则，
∴.
例题3．（2023·全国·高三专题练习）设，求下列各式的值．
(1)；
(2)；
(3)；
(4)；
(5)．
【答案】(1)
(2)﹣2100
(3)
(4)1
(5)
（1）
在中，
令，得．
（2）
令，得  ①，
则.
（3）
令，得  ②，
联立①②，得．
（4）

．
（5）
因为的展开式的通项为，
所以，，，，，，，
所以

．
同类题型演练
1．（2023·高二课时练习）已知，求：
（1）；
（2）；
（3）；
（4）.
【答案】（1）-2；（2）-1094；（3）1093；（4）2187.
【详解】解：令则①；
令则②；
令则③；
（1）②-①得：；
（2）(②-③)得：；
（3）(②+③)得：；
（4）由展开式可知均为负值，均为正值，
则.
2．（2022·全国·高三专题练习），求的值．
【答案】
【详解】因为，
所以令，得．
令，得，
两式相减，得，则，
又因为的二项通项公式为，
当时，得，故，
当时，得，故，
故，
所以．
3．（2022春·河南南阳·高二校考阶段练习）若，其中.
(1)求m的值；
(2)求；
(3)求.
【答案】(1)
(2)
(3)0
【详解】（1）的展开式的通项为，
所以，
所以，解得；
（2）由（1）知，
令，可得，
令，可得，
所以；
（3）令，可得，
由（2）知，
所以

题型8：有关整除或求余问题
典型例题
例题1．（2023·高二课时练习）设，且，若能被13整除，则的值为（    ）．
A．0 B．1 C．11 D．12
【答案】B
【详解】，
且含有因数52，故能被52整除，
要使得能被13整除，且，，
则可得，且，故，.
故选：B
例题2．（2023·全国·高三专题练习）设，且，若能被13整除，则等于（    ）
A．0 B．1 C．11 D．12
【答案】B
【详解】由，展开式通项为，又可以被13整除，
所以展开式中的项均可被13整除，余项为，
要使能被13整除，且，则.
故选：B
例题3．（2023·全国·高三专题练习）若，则被8整除的余数为___________.
【答案】5
【详解】在已知等式中，取得，
取得，
两式相减得，
即，
因为



因为能被8整除，
所以被8整除的余数为5，
即被8整除的余数为5，
故答案为：5.
例题4．（2023·全国·高三专题练习）若，则被4除得的余数为___________.
【答案】1
【详解】由题知，时，①，
时，②，由①+②得，
，
故


所以被4除得的余数是1.
故答案为：1.
同类题型演练
1．（2023·高二课时练习）设a∈Z，且0≤a